【相机标定+测距+动手设计】用matlab标定摄像机以后，用python在标定平面内建立世界坐标系并测距

点击下方卡片，关注“新机器视觉”公众号

视觉/图像重磅干货，第一时间送达

您需要的基础知识：1.相机成像原理2.计算机标定3.Matlab python编程基础

先给大家看看总目录

• 1.1任务要求
• 1.2任务分析

• 2.1相机的成像原理

• 2.2深度的测量原理

• 3.1硬件部分设计

• 3.1.1标定板的制作

• 3.1.2标定图像的制作

• 3.2软件部分设计

• 3.2.1程序总流程图设计

• 3.2.2拍摄图像部分流程图设计

• 3.2.3相机标定的流程图设计

• 3.2.4测量的流程图设计

• 3.2.5计算距离的流程图设计

• 3.3部分重要代码分析

• 3.3.1拍摄部分

• 3.3.2相机内参标定部分

• 3.3.3测量部分

• 4.1程序运行结果

• 4.1.1拍摄部分

• 4.1.2相机标定部分

• 4.1.3测量部分：

• 4.2结果分析

• 4.2.1相机部分

• 4.2.2标定部分

• 4.2.3测量部分

• 4.3总结

• 5.1相机拍照部分代码

• 5.2相机标定部分代码

• 5.3测量部分代码

一、设计任务

1.1 任务要求

摄像机标定使用自制标定板，使用工业摄像机或手机摄像头进行标定。将标定的摄像机内参和外参进行保存。设计测量方案，使用标定过的摄像机对包含垂直边缘的物品（直尺刻度线，矩形物体边缘等）进行距离或边长的测量。标定过程和测量过程，均需要保持摄像机与测量平面之间的距离固定，物品高度不能过高，否则影响测量结果。完成以下设计任务：

系统整体方案设计，包括

结合Halcon（或open CV）软件，写出各功能模块的实现及相应的代码。

• 1. 标定板制作

• 2. 摄像机标定

• 3. 对设计方案中垂直于测量矩形框的直边进行提取，并测量直边之间的距离，从而得到平面测量对象的尺寸
  

• 4. 对测量值与实际尺寸误差进行一定的分析和改进5. 多次测量，计算出测量的平均值和标准差

本次任务主程序可以分为三块：相机拍摄，相机标定，测量三大块。

其中，相机拍摄为相机标定主要任务，是获取图像，存储的是图像的参数；

相机标定的主要任务是获取相机的内参；

在测量里面，我们需要用

标定板来确定相机的外参，

然后由于我们在测量图像外参的时候，

默认将标定板作为参考坐标系，

所以只要将相机成像平面中的点投影到Z=0时的成像平面就可以了。

大致方案如下所示：

二、设计原理

2.1 相机成像原理

我们熟知的摄像机是由光线透过透镜折射，反射到成像平面形成的，

本质是利用二维图像获取三维信息的过程。

所以我们可以通过成像的状况来反映三维世界中的信息。

但是，现实模型总会与理想模型存在一些偏差，

这里的偏差主要就是相机内参与畸变系数所导致的。

由于每一个相机都是利用的透镜成像原理，所以很容易产生桶形畸变或者是枕形畸变。

所以一个三维的图像到OpenCV显示的画面需要经历三个变化，这三个变化对应的参数分别是相机位姿参数，畸变技术，相机内参。

具体的内容，请参看我之前的推文：

相机标定究竟在标定什么？？？

2.2 深度的测量原理

这里我使用的是一个单目摄像机。

如果不移动相机，我们是无法获取三维平面内的尺度信息和深度信息的。

但是我们可以获取三维平面内的比例关系。

这时候我们需要知道更多的参数。在这次的任务里面，我们需要的参数有两个：

一个是相机的位姿参数，一个是成像平面。

知道了这两个参数，我们就可以将摄像机内二维平面内的点投射到三维的坐标中去，再利用三维坐标轻松算出点与点之间的距离。

默认将世界坐标系的原点放在标定板第一个角点上。

所以，我们只需要将成像平面设置为Z=0，即XOY面就可以了，这时我们便获得了需要计算深度信息的所有参数。

三、方案整理及各个功能模块的设计

3.1 硬件部分设计

3.1.1标定板的制作

可能大家不知道Matlab还可以制作标定板吧

cb=(checkerboard(300,4,5)>0.5); figure,imshow(cb);

得到的标定板如下：

将其打印下来，或者放在ipad/pc上，

（这个时候要知道ipad和电脑的尺寸）

3.1.2 标定图像的制作

为了方便测量，我选用了一个红色的长方形来做测量的模块。如下图所示：

实际长度在118.4-118.5毫米。

3.2 软件部分

3.2.1 程序总流程图设计

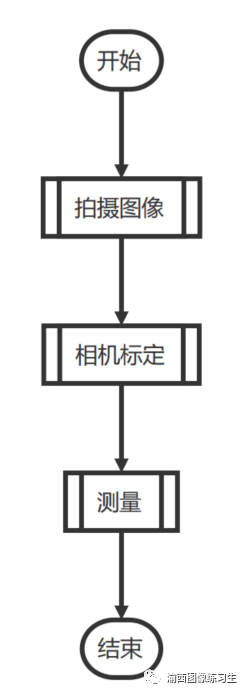
3.2.2 相机标定流程

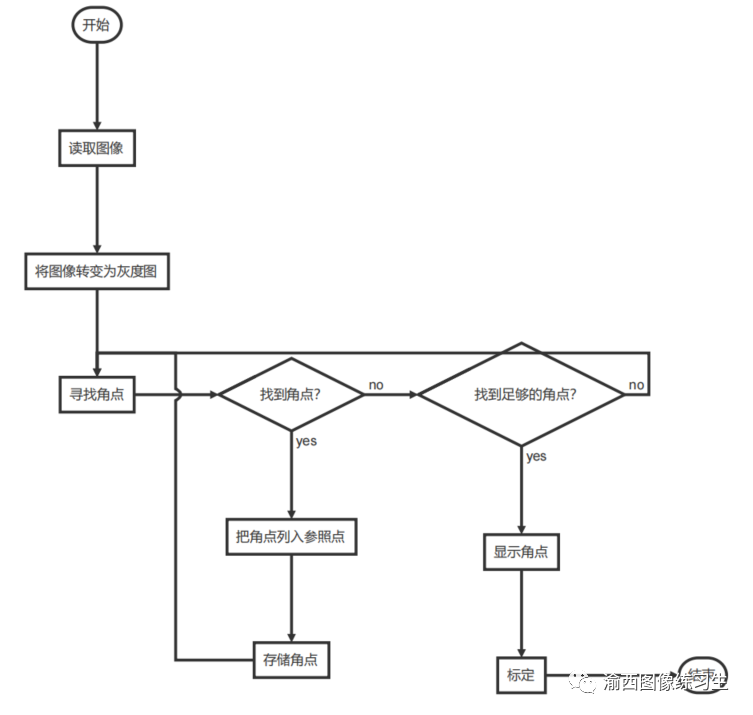
相机标定主要是对棋盘角点的寻找，然后再储存角点，

（这里就需要角点检测的知识，如果不太懂，大家可以去百度一下）

如果储存到了足够多的角点的话，就退出程序的循环，进行标定。

3.2.3 计算距离流程

之前为什么要用红色物体作为被测物体

是因为红色在HSV模式下更容易被分离出来

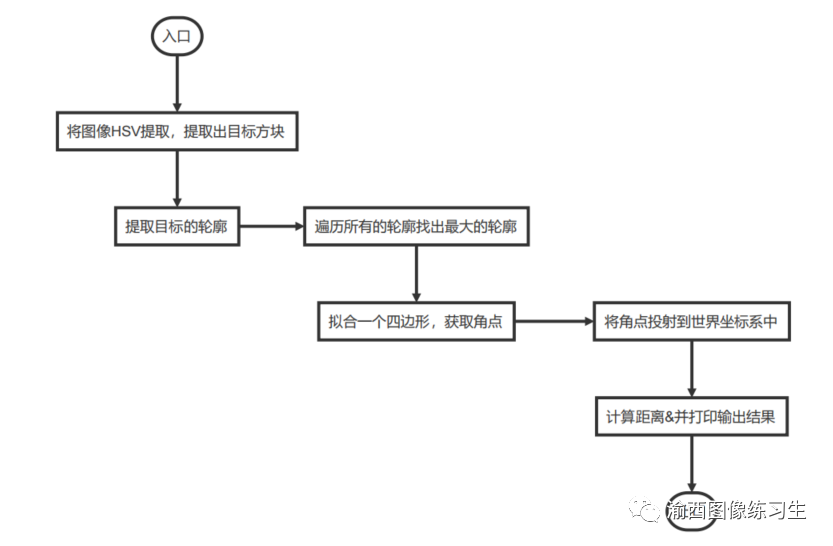
3.3 重要代码部分

拍摄部分

if key == ord('s'):    cv.imwrite(filepath +img_name + str(a)+'.png',frame) # 按s截取图像    a = a + 1 # 改变截取图像的名称 if key == ord('q'):       break # 如果检测到按键为esc，就退出摄像

相机参数标定部分

ret, corners = cv2.findChessboardCorners(gray, (7, 5), None)        # 如果找出角点，把角点加入坐标系内        if ret == True:            objpoints.append(objp * 30)            # 参照criteria进行亚像素检验            corners2 = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)            imgpoints.append(corners2)            # 将角点显示出来            img = cv2.drawChessboardCorners(img, (7, 5), corners2, ret)            cv2.imwrite(sys.path[0] + "/标定结果/" + "result" + str(a) + ".png", img)            a = a + 1

findChessboardCorners是一个检测标定板角点的函数，

如果检测到了角点，

就以criteria的规则进行亚像素检验，

然后再将所有的角点储存下来，

将检测到的角点显示并且将显示角点的图像保存下来。

测量部分

f Find:            # 获取更精确的角点位置(亚像素精度)            exact_corners = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)            # 获取外参，其中rvec是旋转矩阵，tvec是平移矩阵            _, rvec, tvec, inliers = cv2.solvePnPRansac(world_point, exact_corners, IntrinsicMatrix, distC            # 获取两个平面(像素平面与实际平面)的映射关系,其中RMat是相机平面到Z=0轴的投影            Mat = cv2.findHomography(D_2_point, exact_corners)[0]            RMat = cv2.findHomography(exact_corners, D_2_point)[0]
            # print(np.transpose(np.dot(Mat,[[24.575*3,0],[0,24.575*3],[1,1]])))            # 这里打印的是一个投影的值            # 根据3D坐标，获取投影的二维坐标            imgpts, jac = cv2.projectPoints(axis, rvec, tvec, IntrinsicMatrix, distCoeffs)            # 可视化角点，画出图像            img = draw(image, corners, imgpts)            # cv2.imshow('img', img)            return [Mat, RMat, corners, imgpts]

同样的，这里依然进行摄像机标定，

不过这里进行的是摄像机外参的标定，

通过投影的方法找到相机的内参和外参，

再返回一个相机位姿矩阵。

contours, hierarchy = cv2.findContours(image_2, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)for contour in contours:    arclength = cv2.arcLength(contour, True)    # print(arclength)    a.append(arclength) # 长度保存在数组中maxlen = max(a)for contour in contours:    arclength = cv2.arcLength(contour, True)    if arclength == maxlen:        dot = cv2.approxPolyDP(contour,5,True)        dot = np.int0(dot)        cv2.drawContours(image, [dot], 0, (0, 0, 0), 1)

用HSV参数进行阈值化处理后，findContours作用是找出目标物体的外轮廓，返回的contour是轮廓的点集。

考虑到在图像里面会有很多干扰点，所以我们要将最大的轮廓给过滤出来。approxPolyDP表示的是多边形拟合，在这个函数中，返回的是图像中四边形的四个角点。

根据图像里面返回的四个角点，以及相机位姿及其内参，三维空间里平面参数，我们很容易将图像的几个点在三维空间里面描述出来。也就很容易知道四边形对应的矩形几个边的边长了。

四、结果展示和分析

拍出来以下的图像以备相机内参标定：

拍出以下图片准备外参标定：

拍出以下图片准备测量长度：

MATLAB结合标定出来的位姿，

用MATLAB作图如下，一共选取了5张图像作为标定的图像

得到的内参矩阵：

畸变矩阵：

测量结果：

今天的教程就到这里为止了

—版权声明—

仅用于学术分享，版权属于原作者。

若有侵权，请联系微信号:yiyang-sy 删除或修改！