浮点运算为什么不准?有人为0.30000000000000004建了个网站

【新智元导读】计算机浮点运算会出现一定程度的不准确性,通常是.1 + .2!= .3。这个网站解释了为什么计算机会出现这样的情况,以及各种语言出现的不同结果,引发读者热议。浮点运算是计算机基本运算,但是会因为使用的编程语言不同而出现一些奇特的现象。来新智元 AI 朋友圈和AI大咖一起讨论吧~
浮点运算一直非常玄学。
任何一个学过小数点运算的拥有小学数学水平的人,都应该知道 1.0-0.9=0.1。然而当你把这个问题抛给可以计算出圆周率小数点后上百位、拥有超强算力的计算机的时候,结果总是非常迷。
你会发现,使用double或者float得出的计算结果,总是跟我们的预期有一点点差距,这就使得浮点运算容易让人觉得“不精确”。
实际上,因为我们人类理解的数字是十进制,而计算机理解的数字是二进制。比如101.11这个数字,在人类眼中是一百零一点一一,而在电脑看来则是1 * 2^2 +0 *2^1 + 1*2^0 + 1*2^-1 + 1*2^-2 = 4+0+1+1/2+1/4 = 5.75,这个差距着实有点可怕的。
用二进制来表达十进制的小数点,仿佛在接两根口径不一致的管子,就会出现总是对不上的情况。比如为了表示0.2这个十进制下的数字,二进制只能用 1/(2^n)来表示小数,于是:
0.01 = 1/4 = 0.25 ,太大
0.001 =1/8 = 0.125 , 又太小
0.0011 = 1/8 + 1/16 = 0.1875 , 逼近0.2了
0.00111 = 1/8 + 1/16 + 1/32 = 0.21875 , 又大了
0.001101 = 1/8+ 1/16 + 1/64 = 0.203125 还是大
0.0011001 = 1/8 + 1/16 + 1/128 = 0.1953125 这结果不错
0.00110011 = 1/8+1/16+1/128+1/256 = 0.19921875
……
当然,理论上是可以做到无限逼近的。然而我们的物理存储介质的容量毕竟不是无限扩展的,那么在编程语言中就会采用一些取巧的方式来进行权衡。比如java中规定double是32位,float是64位。但无论是多少位,总之是个博弈的结果,并不能完美的解决上述问题,甚至在不同平台、硬件下,同样的操作、同样的位数,得出的结果都可能不一样,更不用说在不同的编程语言环境下了。
比如0.1+0.2,结果如下:

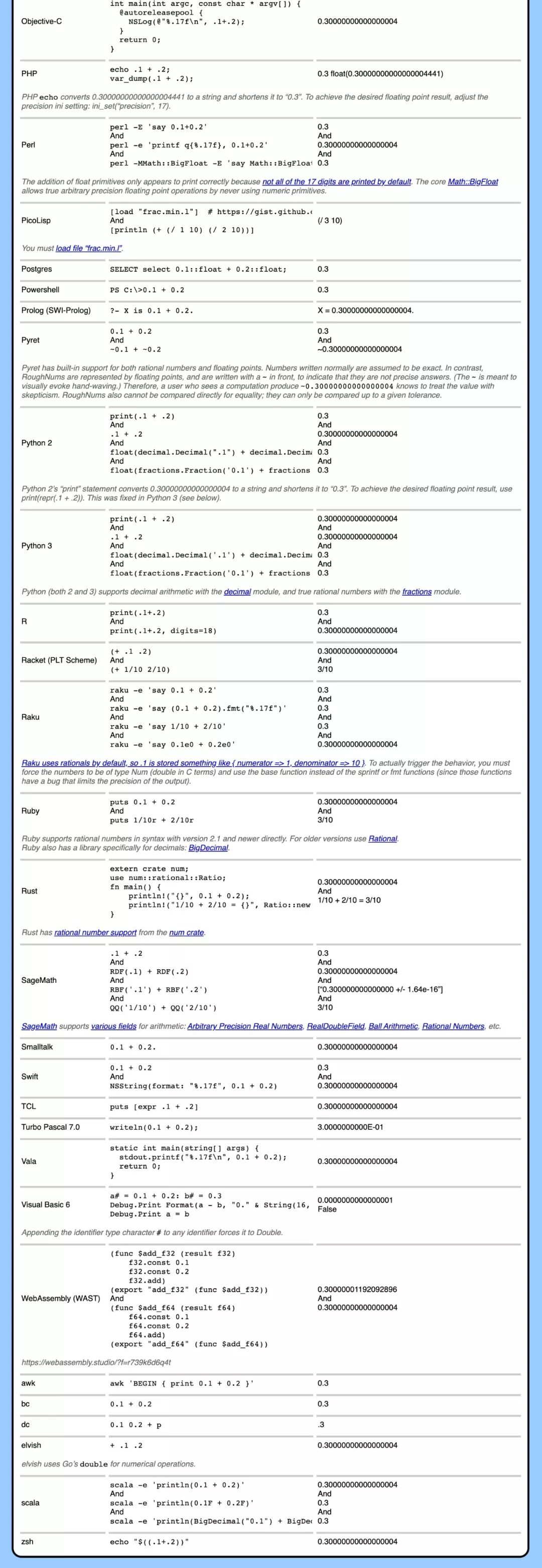
有人因此建立了一个网站:
https://0.30000000000000004.com/
正是因为浮点运算的精度问题,使得其无法应用在像银行这样对数字极度敏感的场景中。银行使用的是定点计算,简单来说,就是把小数转换为整数的一种计算。因为这样操作,所有的账目都是可以预测的。
但浮点运算可以表示比的范围比整数更大、在大数运算中也更有优势,它天生是为表示超大数或者无限值。因此在类似图神经网络这种注重数量大于精度的场景下,才是浮点运算大显身手的地方。

