前言

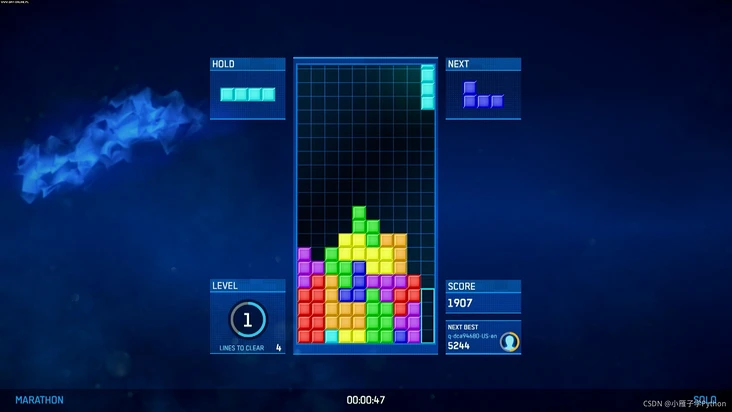
代码效果展示

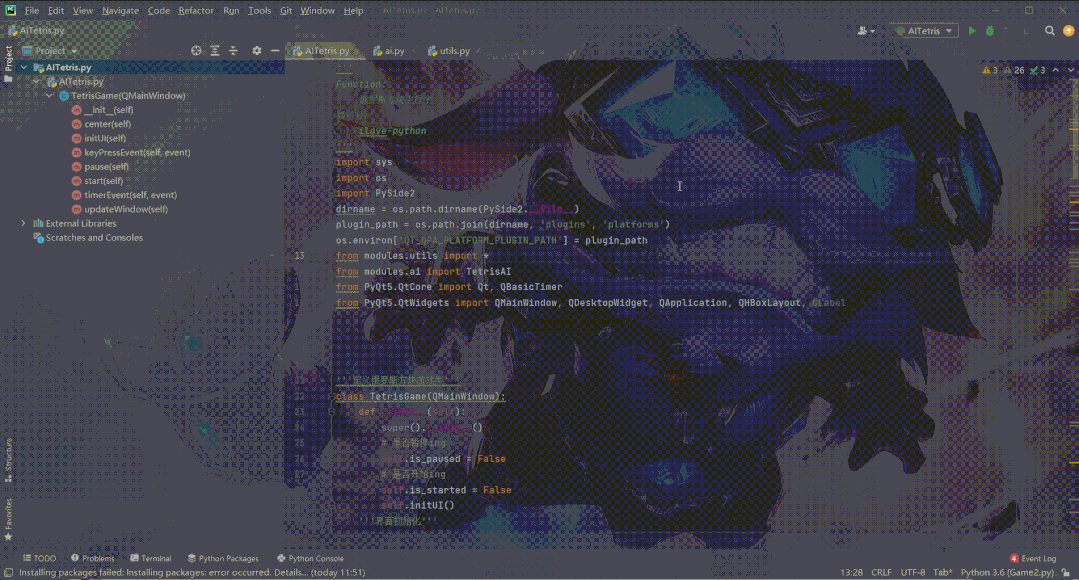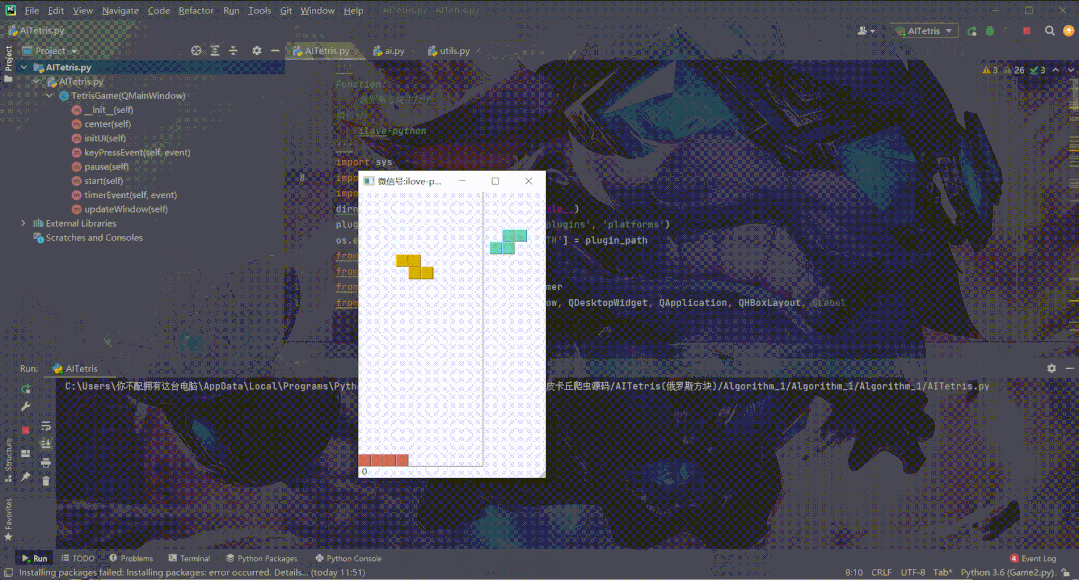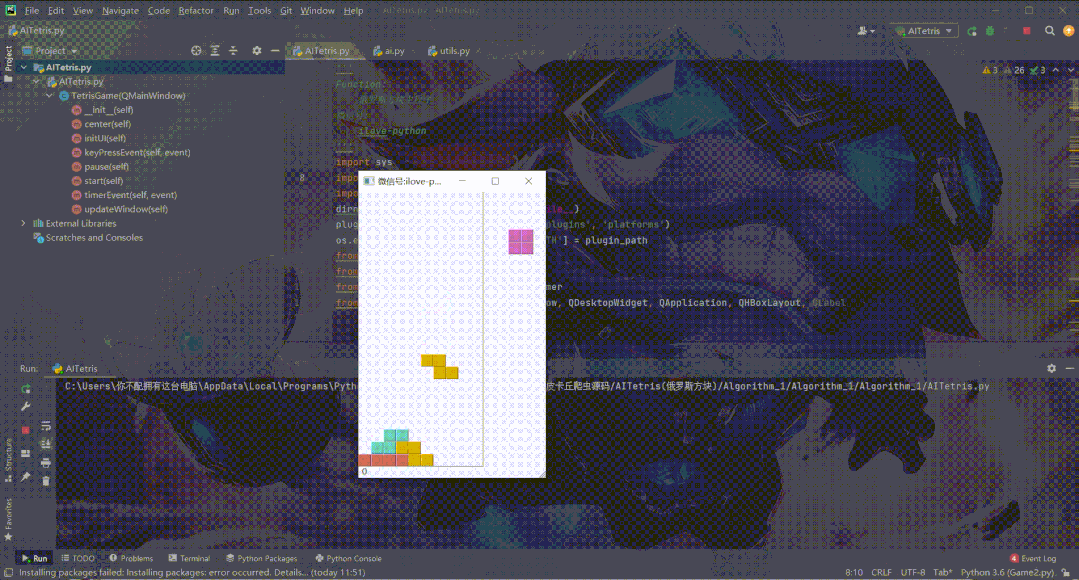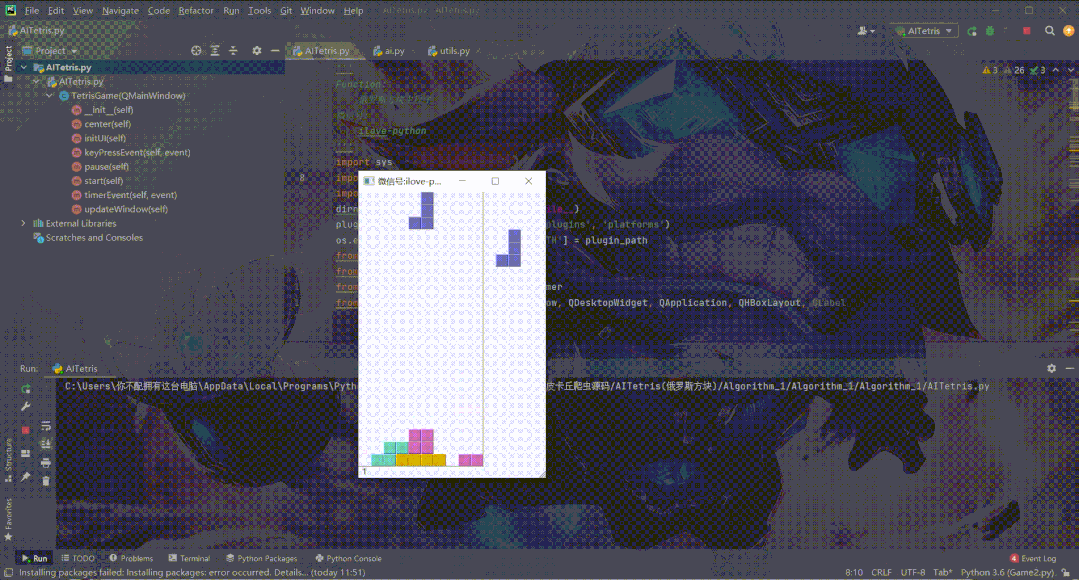
开发工具

环境搭建

原理简介

（1）游戏制作

（2）AI源码实现

# 简单的AI算法
        for d_now in current_direction_range:
            x_now_min, x_now_max, y_now_min, y_now_max = self.inner_board.current_tetris.getRelativeBoundary(d_now)
            for x_now in range(-x_now_min, self.inner_board.width - x_now_max):
                board = self.getFinalBoardData(d_now, x_now)
                for d_next in next_direction_range:
                    x_next_min, x_next_max, y_next_min, y_next_max = self.inner_board.next_tetris.getRelativeBoundary(d_next)
                    distances = self.getDropDistances(board, d_next, range(-x_next_min, self.inner_board.width-x_next_max))
                    for x_next in range(-x_next_min, self.inner_board.width-x_next_max):
                        score = self.calcScore(copy.deepcopy(board), d_next, x_next, distances)
                        if not action or action[2] < score:
                            action = [d_now, x_now, score]
        return action

# 空位统计
        hole_statistic_0 = [0] * width
        hole_statistic_1 = [0] * width
        # 方块数量
        num_blocks = 0
        # 空位数量
        num_holes = 0
        # 每个x位置堆积俄罗斯方块的最高点
        roof_y = [0] * width
        for y in range(height-1, -1, -1):
            # 是否有空位
            has_hole = False
            # 是否有方块
            has_block = False
            for x in range(width):
                if board[x + y * width] == tetrisShape().shape_empty:
                    has_hole = True
                    hole_statistic_0[x] += 1
                else:
                    has_block = True
                    roof_y[x] = height - y
                    if hole_statistic_0[x] > 0:
                        hole_statistic_1[x] += hole_statistic_0[x]
                        hole_statistic_0[x] = 0
                    if hole_statistic_1[x] > 0:
                        num_blocks += 1
            if not has_block:
                break
            if not has_hole and has_block:
                removed_lines += 1
        # 数据^0.7之和
        num_holes = sum([i ** .7 for i in hole_statistic_1])
        # 最高点
        max_height = max(roof_y) - removed_lines
        # roof_y做差分运算
        roof_dy = [roof_y[i]-roof_y[i+1] for i in range(len(roof_y)-1)]
        # 计算标准差E(x^2) - E(x)^2
        if len(roof_y) <= 0:
            roof_y_std = 0
        else:
            roof_y_std = math.sqrt(sum([y**2 for y in roof_y]) / len(roof_y) - (sum(roof_y) / len(roof_y)) ** 2)
        if len(roof_dy) <= 0:
            roof_dy_std = 0
        else:
            roof_dy_std = math.sqrt(sum([dy**2 for dy in roof_dy]) / len(roof_dy) - (sum(roof_dy) / len(roof_dy)) ** 2)
        # roof_dy绝对值之和
        abs_dy = sum([abs(dy) for dy in roof_dy])
        # 最大值与最小值之差
        max_dy = max(roof_y) - min(roof_y)
        # 计算得分
        score = removed_lines * 1.8 - num_holes * 1.0 - num_blocks * 0.5 - max_height ** 1.5 * 0.02 - roof_y_std * 1e-5 - roof_dy_std * 0.01 - abs_dy * 0.2 - max_dy * 0.3
        return score