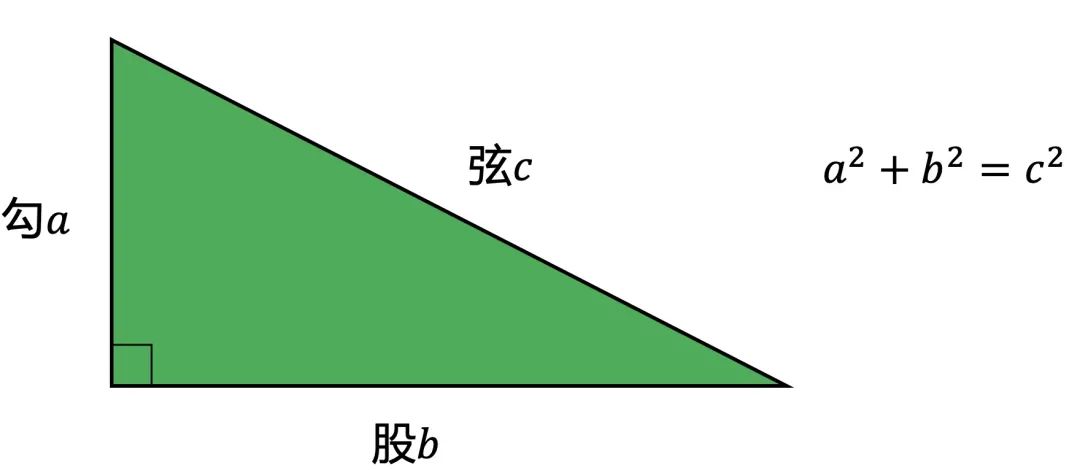
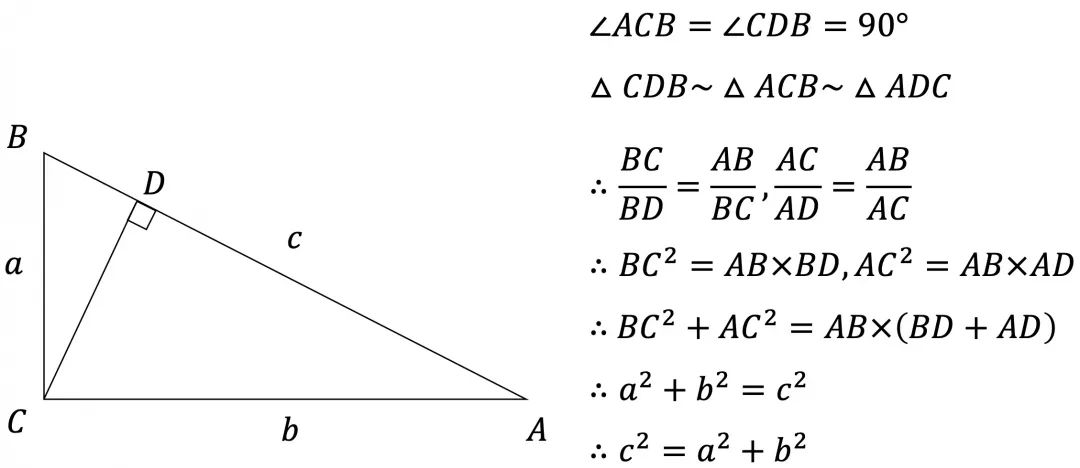勾股定理竟然有500种证明方法,你会几种?

《周髀算经》原文记载:

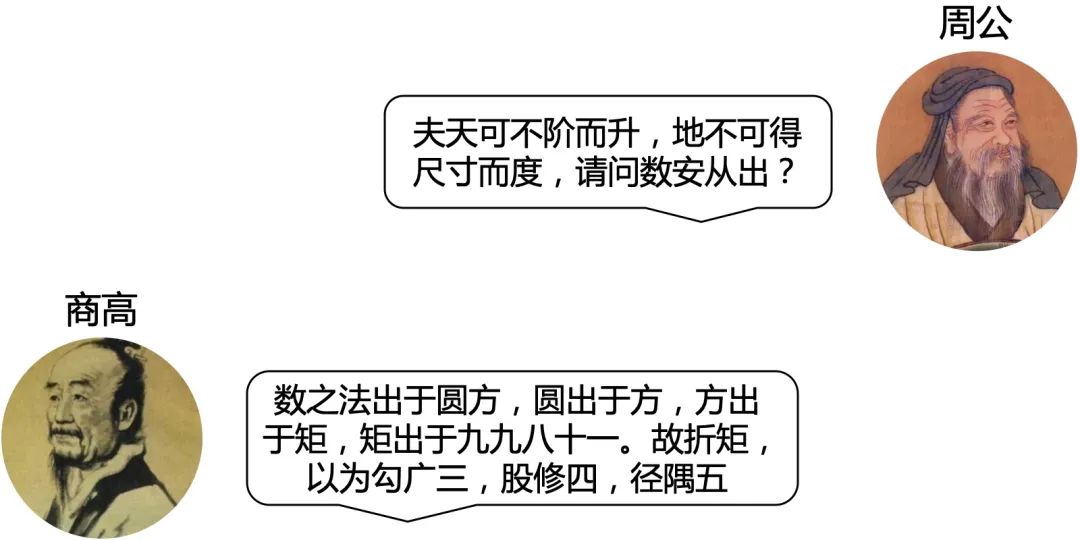
公元前6世纪,古希腊数学家毕达哥拉斯,提出了勾股定理,但证明方法已失传。所以西方多称这个定理为毕达哥拉斯定理。
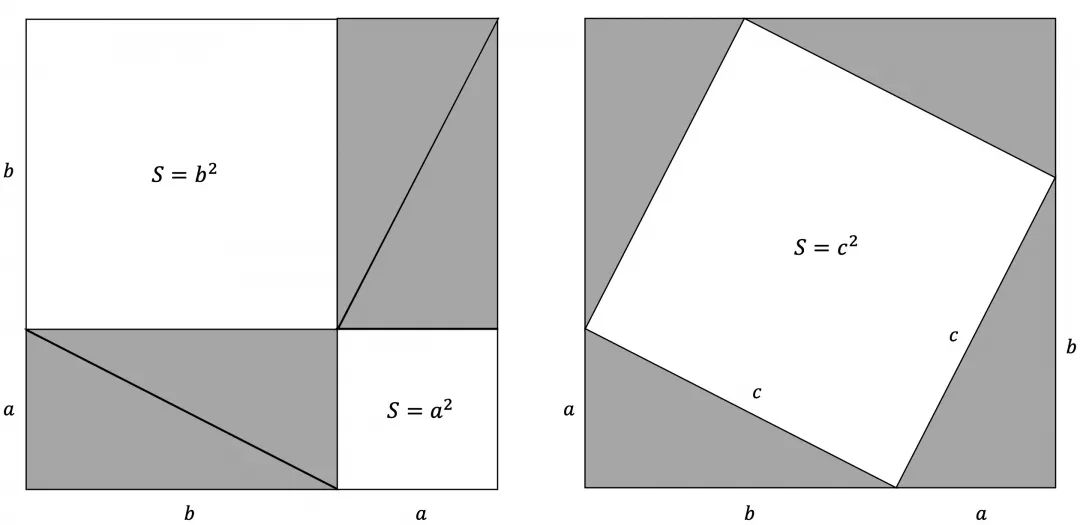
说明:同底等高的长方形面积是三角形面积的2倍,如下同色块的面积是相等的。
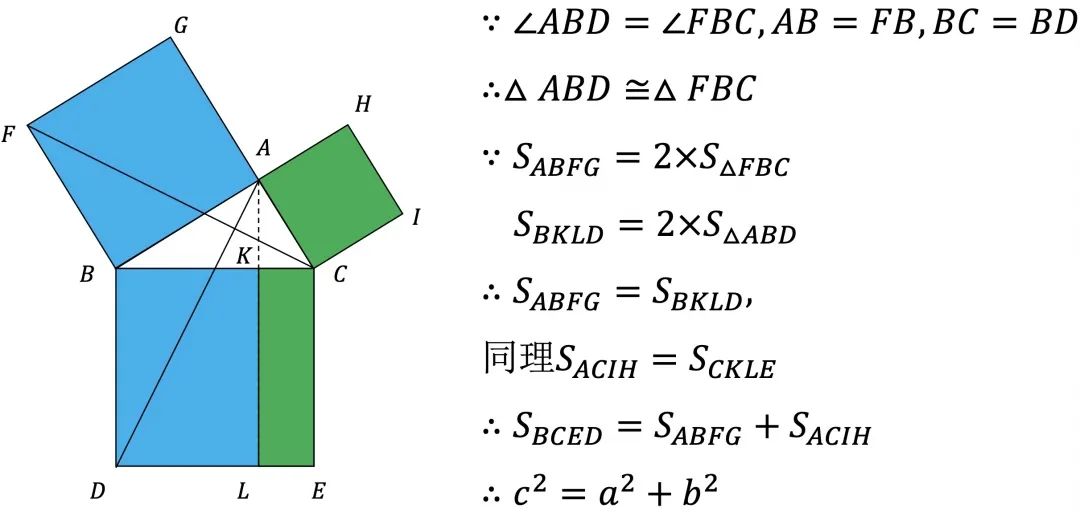
说明:大正方形的面积等于4个直角三角形加上一个小正方形面积之和。
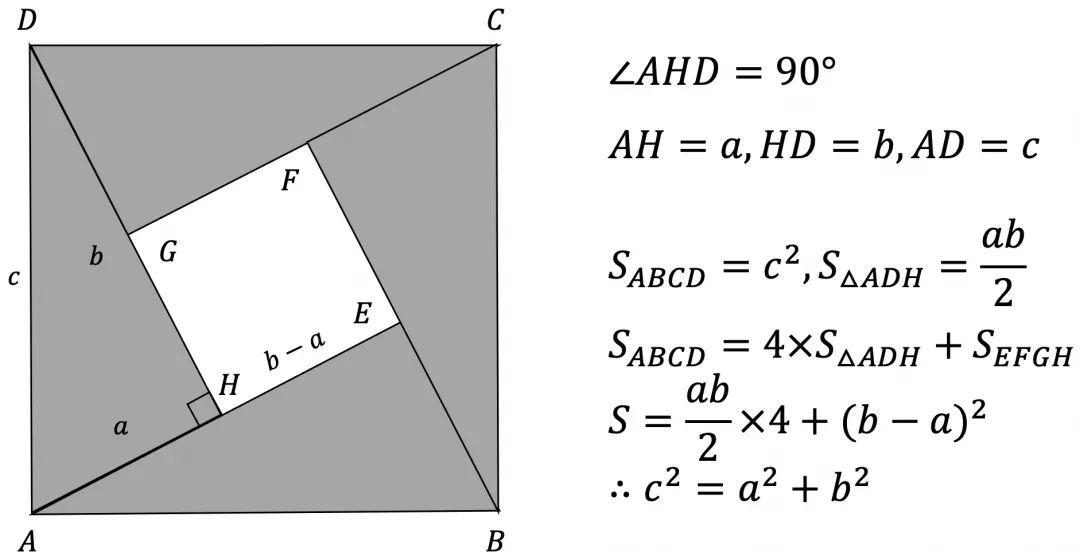
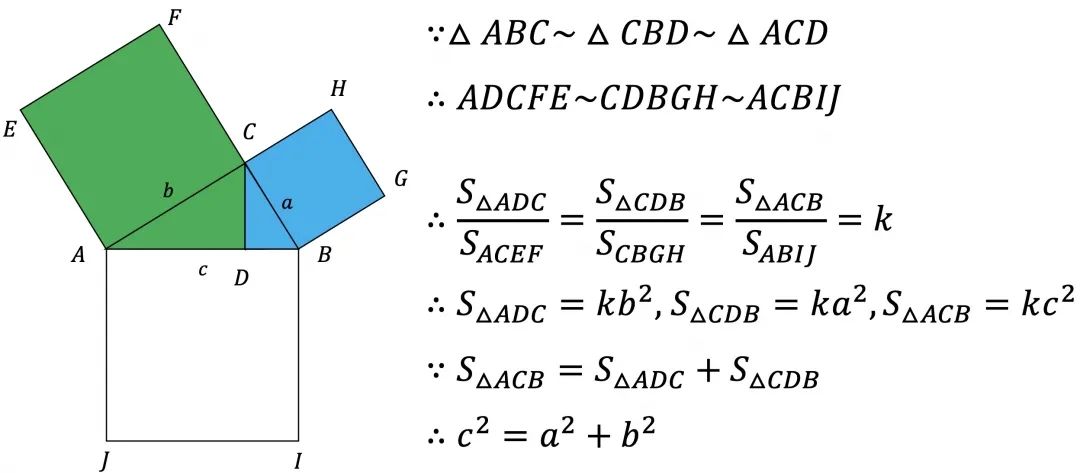
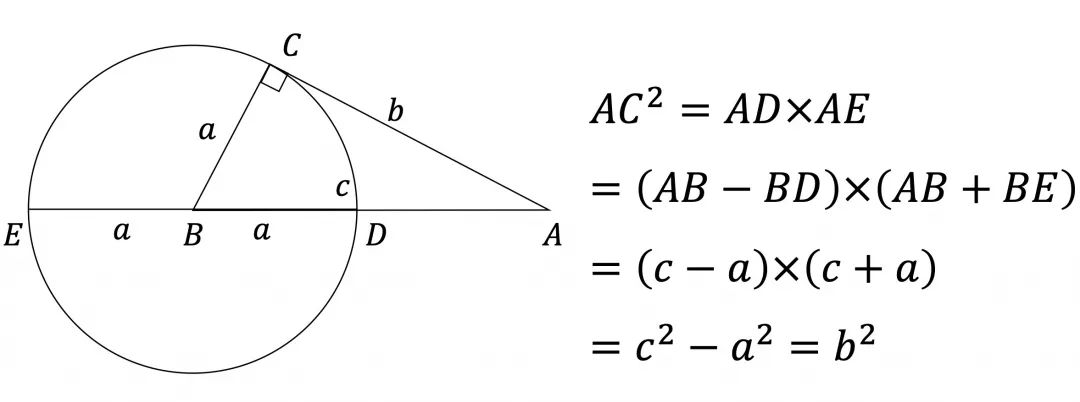
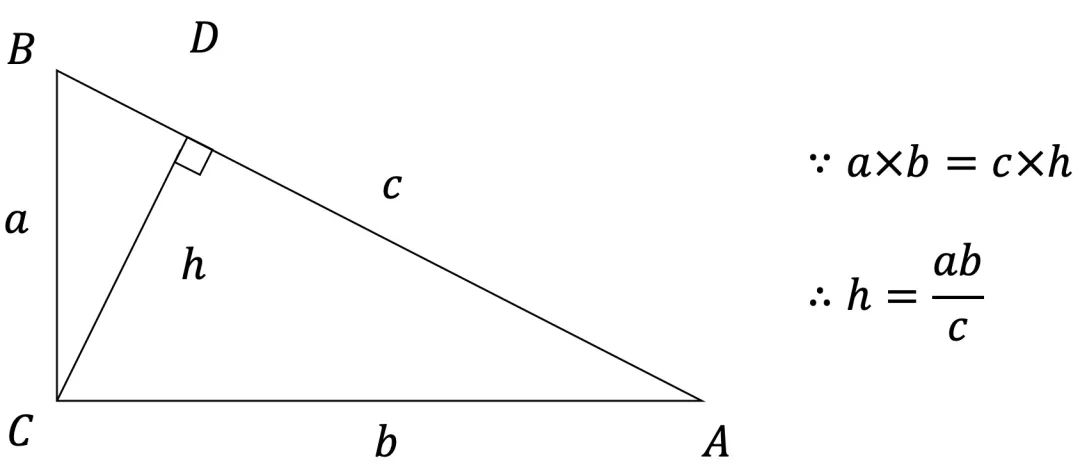
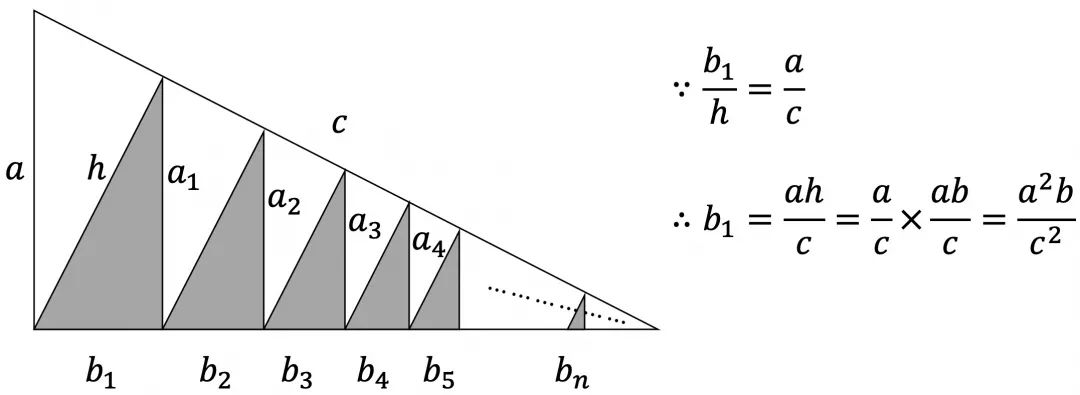
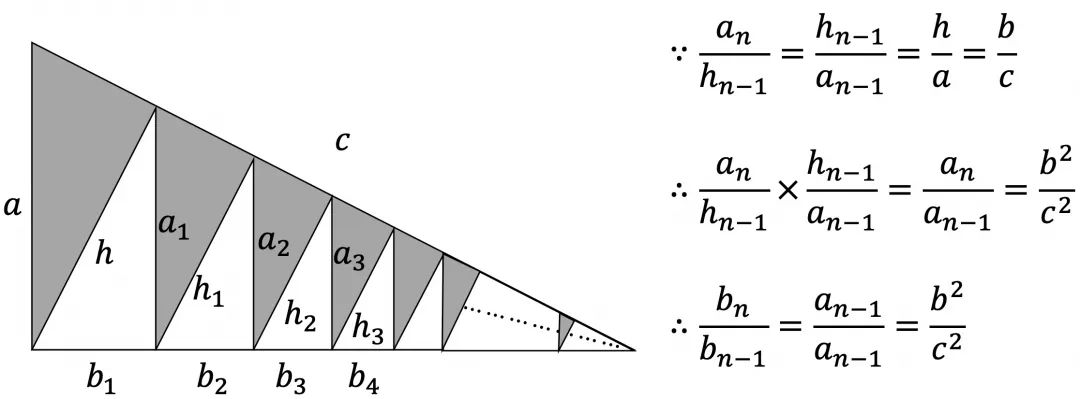
说明:三个直角三角形相似,那么该三角形的面积与以斜边构成的正方形面积之比固定。
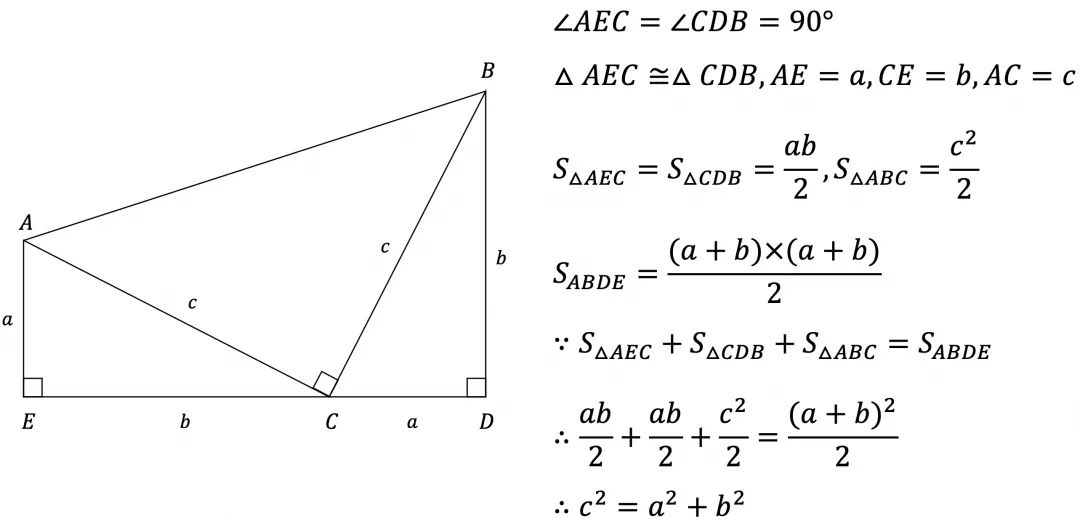
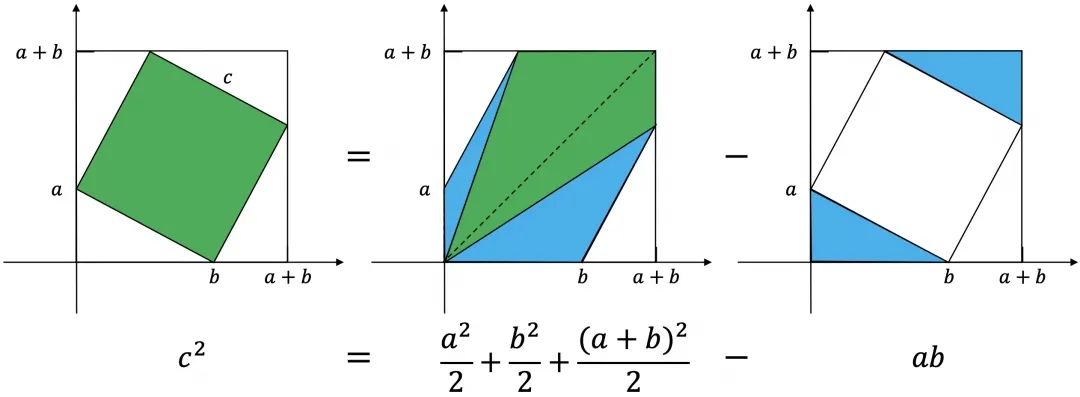
说明:梯形面积等于3个直角三角形的面积之和。
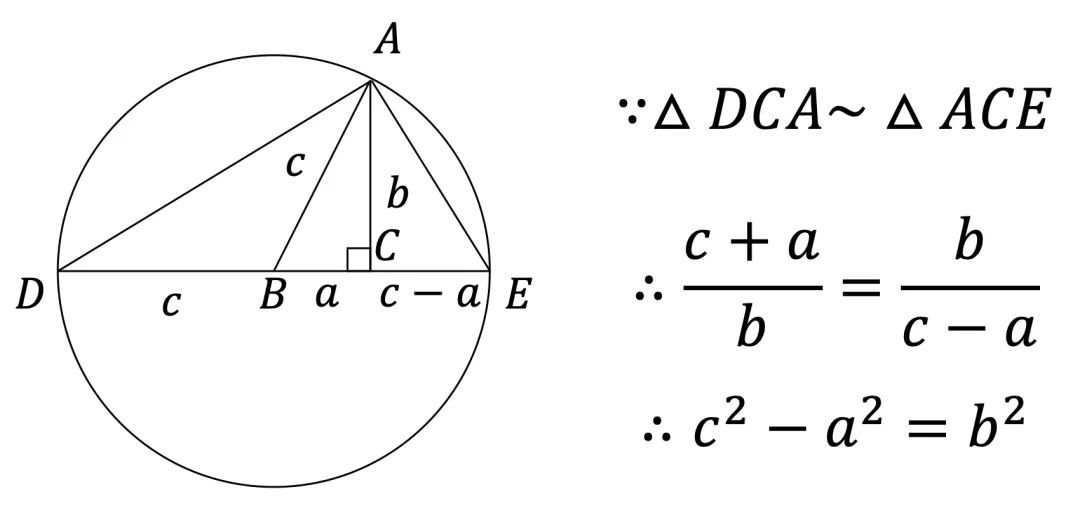
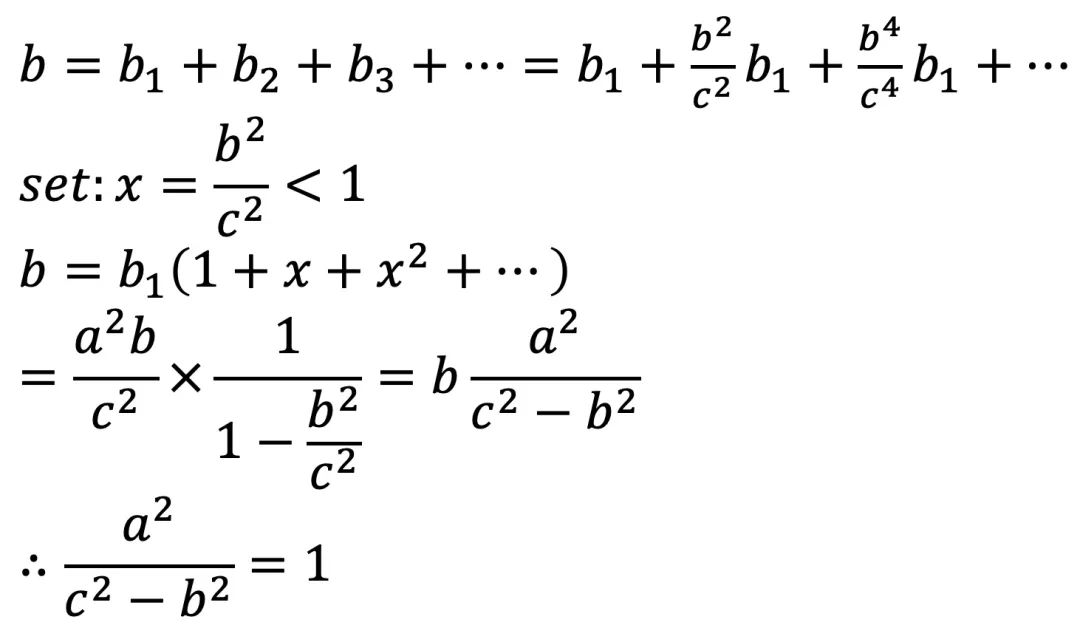


评论
 下载APP
下载APP



公元前6世纪,古希腊数学家毕达哥拉斯,提出了勾股定理,但证明方法已失传。所以西方多称这个定理为毕达哥拉斯定理。