上一篇里忘记说了，为什么取名为矩阵之芯呢？

除了这东西在线性代数里确实比较重要外，从长相看，是不是有点上面图片里的那家伙的身形。矩阵的奇异值分解，一分为仨，中间露出芯，是不是有几分开心果脱壳而出的神韵。

1基本性质

上一篇最后讨论了左右奇异向量具有如下性质，

\begin{aligned} \mathbf{A} \mathbf{v}_{i} &=\sigma_{i} \mathbf{u}_{i}\\[0.8em] \mathbf{A}^{\top} \mathbf{u}_{i} &=\sigma_{i} \mathbf{v}_{i} \end{aligned}

对于成立。

今天来看看另一个简单但是也挺有用的性质。

令具有奇异值分解，该分解具有下列基本性质，

1、秩，等于的非零奇异值的数量。
2、由左右奇异向量

\mathbf{U}=\left[\mathbf{u}_{1}, \ldots, \mathbf{u}_{m}\right]

和

\mathbf{V}=\left[\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\right]

可以构建的外积展开式，

\mathbf{A}=\sum_{i=1}^{r} \sigma_{i} \mathbf{u}_{i} \mathbf{v}_{i}^{\top}.

验证

\begin{aligned} \mathbf{A}&=\mathbf{U} \mathbf{\Sigma V}^{\top}\\[1em] &=\mathbf{U}_{1} \mathbf{S V}^{\top}_1\\[1em] &=\left[\begin{array}{llll} \mathbf{u}_{1} & \mathbf{u}_{2} & \cdots & \mathbf{u}_{r} \end{array}\right]\left[\begin{array}{cccc} \sigma_{1} & & & \\ & \sigma_{2} & & \\ & & \ddots & \\ & & & \sigma_{r} \end{array}\right]\left[\begin{array}{c} \mathbf{v}_{1}^{\top} \\ \mathbf{v}_{2}^{\top} \\ \vdots \\ \mathbf{v}_{r}^{\top} \end{array}\right]\\[1em] &=\left[\begin{array}{llll} \mathbf{u}_{1} & \mathbf{u}_{2} & \cdots & \mathbf{u}_{r} \end{array}\right]\left[\begin{array}{c} \sigma_{1} \mathbf{v}_{1}^{\top} \\ \sigma_{2} \mathbf{v}_{2}^{\top} \\ \vdots \\ \sigma_{r} \mathbf{v}_{r}^{\top} \end{array}\right]\\[1em] &=\sum_{i=1}^{r} \sigma_{i} \mathbf{u}_{i} \mathbf{v}_{i}^{\top} \end{aligned}

注意，最后那个等号对应的式子很有意思，两个矩阵的乘积可以记为两个向量的内积形式。这里，向量都默认写为列向量的形式。

对矩阵乘法的不同理解

上面分解里虽然有三个矩阵，但我们只需要看两个矩阵的乘法。

1、矩阵乘法的第一种理解，即乘积结果的第行、第列元素的值为矩阵的第行与矩阵的第列（都看成向量）的内积，

\begin{aligned} c_{ij}=\sum_{k=1}^{n} a_{ik} b_{kj} \end{aligned}

从上面式子可以看出来，每个元素都是个乘积之和。

2、矩阵乘法的第二种理解，先由矩阵的第列乘以矩阵的第行（都看成矩阵，用矩阵乘法，或者称为向量的外积），结果是一个矩阵，

\begin{aligned} \mathbf{a}_{\star k} \mathbf{b}_{k \star}&=\left[\begin{array}{c} a_{1 k} \\ a_{2 k} \\ \vdots \\ a_{m k} \end{array}\right]\left[\begin{array}{llll} b_{k 1} & b_{k 2} & \cdots & b_{k l} \end{array}\right]\\[1em] &=\left[\begin{array}{c} a_{1 k}b_{k 1} & a_{1 k}b_{k 2} & \cdots & a_{1 k}b_{k l} \\ a_{2 k}b_{k 1} & a_{2 k}b_{k 2} & \cdots & a_{2 k}b_{k l} \\ \vdots \\ a_{m k}b_{k 1} & a_{m k}b_{k 2} & \cdots & a_{m k}b_{k l} \end{array}\right] \end{aligned}

再观察，乘积在位子上的元素为，

\begin{aligned} c_{ij}=\sum_{k=1}^{n} a_{ik} b_{kj} \end{aligned}

所以，将下面这个矩阵加起来

\{\mathbf{a}_{\star 1} \mathbf{b}_{1 \star}, \mathbf{a}_{\star 2} \mathbf{b}_{2 \star}, \cdots, \mathbf{a}_{\star n} \mathbf{b}_{n \star}\}

就是矩阵，即有，

\begin{aligned} \mathbf{AB} = \left[\begin{array}{llll} \mathbf{a}_{\star 1} & \mathbf{a}_{\star 2} & \cdots & \mathbf{a}_{\star n} \end{array}\right]\left[\begin{array}{c} \mathbf{b}_{1 \star} \\ \mathbf{b}_{2 \star} \\ \vdots \\ \mathbf{b}_{n \star} \end{array}\right] =\sum_{i=1}^{n} \mathbf{a}_{\star i} \mathbf{b}_{\star i} \end{aligned}

§外积展开式

上面性质也可以如下展开，

\begin{array}{lll} \mathbf{A}&=\mathbf{U} \mathbf{\Sigma V}^{\top}\\[0.8em]&=\mathbf{U}_1 \mathbf{S V}^{\top}_1\\[0.8em]&=\sigma_{1} \mathbf{u}_{1} \mathbf{v}_{1}^{\top}+\sigma_{2} \mathbf{u}_{2} \mathbf{v}_{2}^{\top}+\cdots+\sigma_{r} \mathbf{u}_{r} \mathbf{v}_{r}^{\top} \end{array}

这里，每一项其实是一个秩为 1 的矩阵，称为秩 1 矩阵。

2简单应用

这一条简单的性质有什么用呢？

我们知道，是从大到小排列的，排在后面的值可能很小了，那算出来的秩 1 矩阵的值也就很小了，对最终元素的贡献可能极其微小。因此，是不是可以考虑丢弃一部分呢？

这一点对应的其实就是下面这个低秩矩阵近似问题。

§低秩矩阵近似

一些实际应用需要求解矩阵的近似矩阵问题，即求一个具有特定秩的截断矩阵。这其实对应一个最优化问题，即基于约束下，求使得两个矩阵差值的 Frobenius 范数最小的矩阵。可以证实，由的 SVD 分解可以给出这个问题的解，即

\tilde{\mathbf{M}}=\mathbf{U} \tilde{\mathbf{\Sigma}} \mathbf{V}^{\top}

其中，对角矩阵来自矩阵，只是它只包含了个最大的奇异值（其他奇异值替换为零）。这就是所谓的 Eckart-Young 定理，这是由两位作者于 1936 年证明的。

不过这里有个问题，就是这个选多少呢？有个简单思路，通过计算前个奇异值之和占所有奇异值总和的一定比例，如，

\min_{k} \frac{\sum_{i=1}^{k} \sigma_{i}}{\sum_{i=1}^{r} \sigma_{i}}>p\;\! \%

那么就选这前个奇异值来重构矩阵，即

\mathbf{A} \approx \mathbf{U}_{m \times k} \mathbf{\Sigma}_{k \times k} \mathbf{V}_{k \times n}^{\top}.

我们将图像灰度看成一个矩阵，然后把它分解了，丢掉一部分重新合成一张图像，看看如何效果。这个例子应该到处都可以看到吧，再来温习一下。

我们来处理一种味道不错的水果（猜猜这是哪个品种）的图像。

import numpy as np
from PIL import Image

import matplotlib.pyplot as plt

plt.style.use('ggplot')

def load(pic):
    i = Image.open(pic)
    g = i.convert('L')
    mat = np.array(g).astype(np.uint8)

    return mat

mat = load('orange.png')

plt.figure(figsize=(10, 5))
plt.imshow(mat, cmap='gray')
plt.show()

U, Sigma, V = np.linalg.svd(mat)

U.shape, Sigma.shape, V.shape

((383, 383), (383,), (492, 492))

看看只保留奇异值最大的那个秩 1 矩阵。

k = 1
re_img = U[:, :k] @ np.diag(Sigma[:k]) @ V[:k, :]

plt.figure(figsize=(10, 5))
plt.imshow(re_img, cmap='gray');

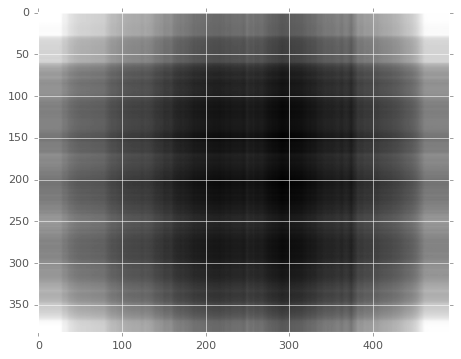
灰蒙蒙一片啊，那就再多看几个。下面我们来按照百分比来自动计算这个值。

def select_k(sigma, pcent):
    s = np.add.accumulate(sigma)
    s = s/s[-1]
    return np.where((s>=pcent)==True)[0][0]

select_k(Sigma, 0.9)

前 85 个奇异值就占了百分之九十的信息量。

# 查看前百分之 70、80、90、100 的重建效果
for i in [select_k(Sigma, 0.7), select_k(Sigma, 0.8), select_k(Sigma, 0.9), select_k(Sigma, 1.0)]:
    re_img = U[:, :i] @ np.diag(Sigma[:i]) @ V[:i, :]
    
    plt.figure(figsize=(10, 5))
    plt.imshow(re_img, cmap='gray')
    title = "n = %s" % i
    plt.title(title)
    plt.show()

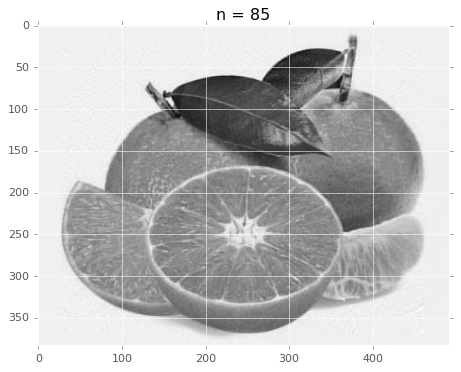
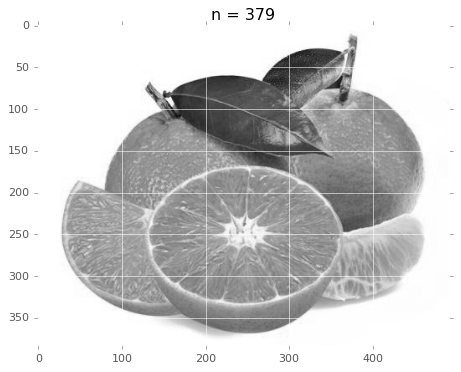
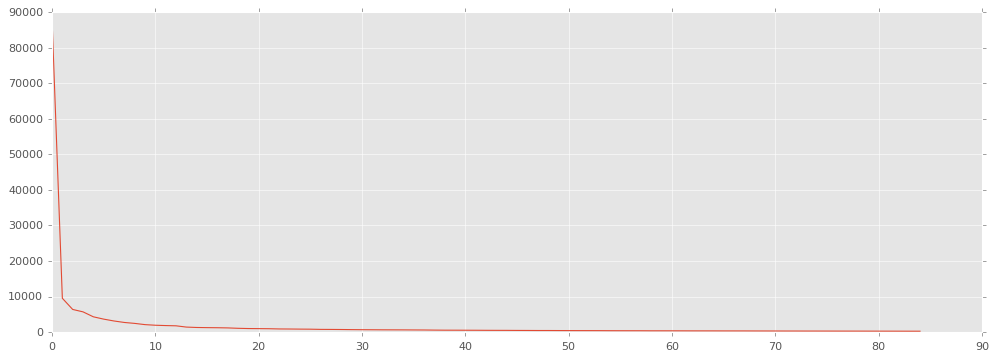
有没有发现，用 85 个秩 1 矩阵生成的结果跟原图差别不大吧。把前 85 个奇异值画出来看看。

plt.figure(figsize=(15, 5))
plt.plot(Sigma[:85]);

3与其他分解的关系

§与特征分解的关系

从可以应用于任何矩阵的意义上讲，奇异值分解具有更广的普适性，而特征分解（谱分解）只能适用于可对角化的矩阵。但是，这两个分解是相关的。

给定的 SVD 分解，以下两个关系成立，

\begin{aligned} \mathbf{A}^{\top} \mathbf{A} &=\mathbf{V} \mathbf{\Sigma}^{\top} \mathbf{U}^{\top} \mathbf{U} \mathbf{\Sigma} \mathbf{V}^{\top}=\mathbf{V}\left(\mathbf{\Sigma}^{\top} \mathbf{\Sigma}\right) \mathbf{V}^{\top}=\mathbf{V} \mathbf{\Sigma}^{2} \mathbf{V}^{\top} \\[1em] \mathbf{A A}^{\top} &=\mathbf{U \Sigma V}^{\top} \mathbf{V \Sigma}^{\top} \mathbf{U}^{\top}=\mathbf{U}\left(\mathbf{\Sigma\Sigma}^{\top}\right) \mathbf{U}^{\top}=\mathbf{U} \mathbf{\Sigma}^{2} \mathbf{U}^{\top} \end{aligned}

上面等式的右边是左边的特征分解。具体来说，

的列（右奇异向量）是的特征向量。
的列（左奇异矢量）是的特征向量。
的非零元素（非零奇异值）是或的非零特征值的平方根。

正规矩阵

正规矩阵定义: 对于复数值方阵，如果，其中是共轭转置，那么矩阵是正规矩阵。

\begin{array}{ccc} &\text{复值方阵}\; \mathbf{A} \;\text{可以分解为}\; \mathbf{A}=\mathbf{U \Lambda U}^{\dagger} \\ &\Downarrow\\ &\mathbf{A} \;\text{是正规矩阵} \end{array}

其中，是酉矩阵，即，并且是对角矩阵。的特征向量对应相应的特征值。

而下面分解

\mathbf{A}=\mathbf{U \Lambda U}^{\dagger}

也被称为矩阵的酉对角化。

如果为 Hermitian 矩阵，则仅具有实值元素。

如果限于一个酉矩阵，则将其所有值放在复数单位圆上，即。

在实数域内，如果是正规矩阵，即

\mathbf{A}^{\top} \mathbf{A}=\mathbf{A A}^{\top}

根据谱定理可知该类矩阵可以使用特征向量对它进行对角化，因此可以将其写为，其中为正交矩阵以及为对角矩阵。

当是半正定时，分解同时也是奇异值分解。否则，可以通过将矩阵每个对角线元素的符号移至其对应的来将其改造为 SVD 分解。

实对称矩阵

作为一种更特殊的情况，对于每个实对称矩阵，特征值都是实数，特征向量可以都是实数并且正交的。因此，实对称矩阵可分解为

\mathbf{A}=\mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{\top}

其中，是正交矩阵，其列是的特征向量，而是对角矩阵，其元素是的特征值。

其展开式跟 SVD 分解也有类似形式，

\begin{array}{lll} \mathbf{A}&=\mathbf{Q} \mathbf{\Lambda Q}^{\top}\\[1em] &=\lambda_{1} \mathbf{q}_{1} \mathbf{q}_{1}^{\top}+\lambda_{2} \mathbf{q}_{2} \mathbf{q}_{2}^{\top}+\cdots+\lambda_{r} \mathbf{q}_{r} \mathbf{q}_{r}^{\top} \end{array}

一般矩阵的特征分解

除了半正定正规矩阵外，的特征分解和 SVD 有所不同。

特征分解为，其中不一定为正交矩阵，而不一定为半正定，而为，其中是对角且为半正定，而和均为正交矩阵。

另外，只有具有完备特征向量集的方阵具有特征分解，但是任何矩阵都具有 SVD 分解。

例子

给定如下实矩阵，

\mathbf{A} = \left[\begin{array}{ll} 1 & 0 \\ 1 & 3 \end{array}\right]

可以求得对进行特征分解所需的矩阵为，

\mathbf{Q}=\left[\begin{array}{cc} -2 c & 0 \\ c & d \end{array}\right], \quad c, d \in \mathbb{R}

即有，

\left[\begin{array}{cc} -2 c & 0 \\ c & d \end{array}\right]^{-1}\left[\begin{array}{ll} 1 & 0 \\ 1 & 3 \end{array}\right]\left[\begin{array}{cc} -2 c & 0 \\ c & d \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 3 \end{array}\right], \quad c, d \in \mathbb{R}

§一般矩阵

SVD 与不能作特征分解的更一般的矩阵之间的联系则可以通过极分解来建立，例如在实数域，可以构建如下分解

\mathbf{A} = \color{blue}{\mathbf{U\Sigma U}^{\top}}\color{green}{\mathbf{U V}^{\top}} = \color{blue}{\mathbf{UV}^{\top}} \color{green}{\mathbf{V\Sigma V}^{\top}}=\mathbf{S R}

其中，是半正定以及正规矩阵，而是正交矩阵。或者，以及。

相关阅读

矩阵和线性代数原来是这么来的

矩阵特征值的故事 - 缘起琴弦

二次型和矩阵合同原来是这么一回事

矩阵特征值是这么来的，以及有趣的盖尔圆

万能的 SVD 分解是哪位牛人提出来的？

度量、范数和内积原来是这么个关系

线性映射: 从凯莱引入矩阵乘法说起

矩阵之芯 SVD: 奇异值分解及其几何解释

矩阵之芯 SVD: 基本应用以及与其他分解的关系