详解 Deep Learning 中的各种激活函数-技术圈

1. 什么是激活函数？

在神经网络中，一个节点的激活函数定义了给定输入或一组输入的输出。一个标准的集成电路可以看作一个由激活函数组成的数字网络，根据输入可以“开”（1）或“关”（0）。这类似于神经网络中的线性感知机。然而只有非线性激活函数才能使这种网络只用少量的节点来计算非线性问题。

在深度学习中，我们之所以要使用诸如 ReLU，Sigmoid 以及 Tanh 等激活函数是为了增加一个非线性属性。通过这种方式，得到的网络可以模拟数据更复杂的关系和模式，拥有更好的泛化能力。

1.1. 回顾：前向传播

为了理解激活函数的重要性，我们先回顾一个神经网络如何计算一个预测/输出。这通常称为前向传播。在前向传播过程中，神经网络收到输入向量并得到一个预测输出向量。考虑以下具有一个输入、一个输出和三个隐藏层的神经网络：网络的层之间通过权值矩阵连接，该网络拥有 4 个权值矩阵以及。

给定一个输入向量，我们计算与第一个权重矩阵的点乘并且应用激活函数处理计算结果，得到的代表第一层神经元的值并作为下一层的输入重复上述操作。直到得到最后输出向量，其代表了神经网络的预测值。

整套操作可以用以下公式表示，其中代表一个任意的激活函数:

1.2 将神经网络看成一个函数

在这一点上，讨论另一种可以用来描述神经网络的解释。与其把神经网络看作是一个节点和边缘的集合，我们可以简单地把它称为一个函数。就像任何常规的数学函数一样，神经网络执行了从输入到输出的映射。

在神经网络的情况下，相应函数的参数是权重。这意味着我们在训练神经网络时的目标是找到一组特定的权重或参数，以便给定特征向量，我们可以计算出一个与实际目标值相对应的预测结果。或者换句话说，我们正试图建立一个能够为我们的训练数据建模的拟合函数。

一个问题是，我们能一直对数据进行建模吗？我们总能找到定义一个函数的权重，该函数可以为给定的特征计算出一个特定的预测值吗？答案是否定的。只有当特征和标签之间存在数学上的相关性时，我们才能对数据进行建模。这种数学上的相关性可以有不同的复杂性。而在大多数情况下，我们看数据的时候，无法用直接得到这种关系。然而，如果在特征和标签之间存在某种数学上的依赖关系，在神经网络的训练过程中，网络会识别这种依赖关系，并调整其权重，以便在训练数据中模拟这种依赖关系。或者换句话说，这样它就可以实现从输入特征到输出的数学映射。

1.3 激活函数的作用

激活函数的目的是为函数添加某种非线性属性，这就是神经网络。如果没有激活函数，神经网络只能进行从输入到输出的线性映射.因为如果没有激活函数，前向传播过程中唯一的数学操作就是输入向量和权重矩阵之间的点乘。

由于单个点积是一个线性运算，连续的点积将只不过是一个接一个重复的多个线性运算。而连续的线性运算可以转换为一个单一的线性运算。

为了增加网络的泛化能力，神经网络必须能够接近从输入特征到输出标签的非线性关系。通常情况下，我们试图从中学习的数据越复杂，特征到标签的映射就越非线性。一个没有任何激活函数的神经网络将无法在数学上实现复杂的映射，也无法解决我们希望网络解决的任务。

2. 不同的激活函数

2.1 Sigmoid

通常最常见的激活函数是 sigmoid 函数。sigmoid 函数将传入的输入映射到 0 和 1 之间的范围：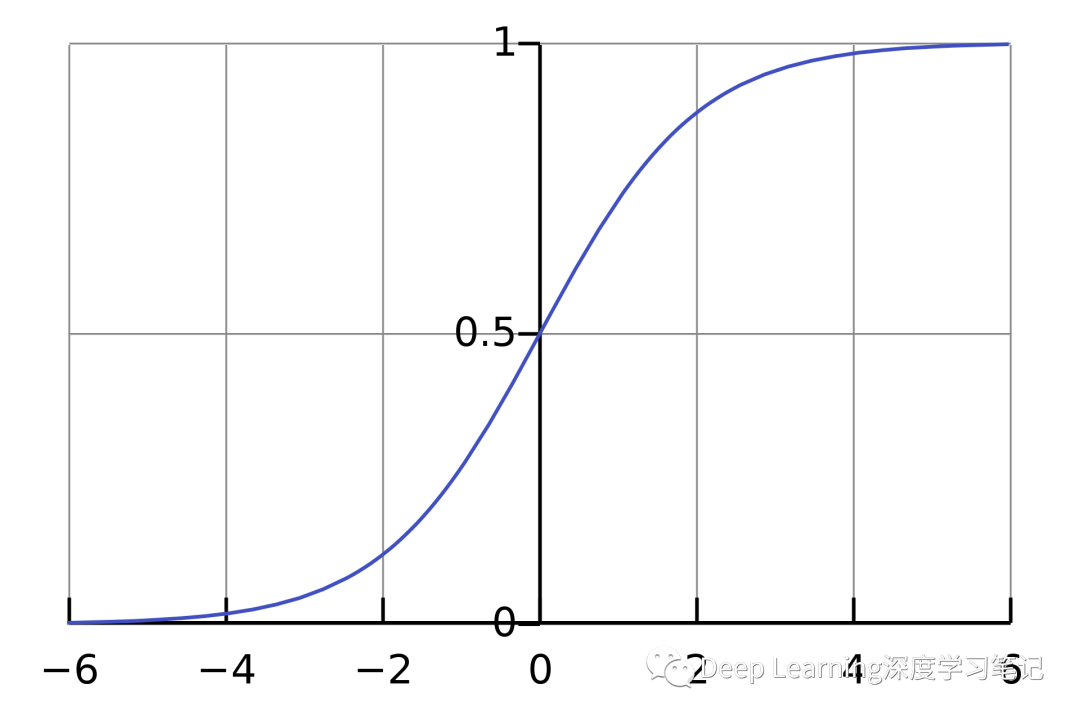

Sigmoid 函数定义如下：

在实践中，sigmoid 非线性特性最近已不再受青睐，它很少被使用。它有两个主要的缺点：

梯度消失：神经元的激活在 0 或 1 的尾部过分稠密，接近 0 的导数会使得损失函数的梯度非常小，导致梯度消失的问题。
非 0 点对称：Sigmoid 的另一个不理想的特性是，该函数的输出不是以零为中心的。通常情况下，这使得神经网络的训练更加困难和不稳定。这里有一个小例子：，其中和是上一层经过 Sigmoid 的输出，所以和总是非零正数。根据整个表达式的梯度，相对于和的梯度将始终是正值或始终为负值。通常情况下，最佳梯度下降步骤需要增加和减少。因此，由于和总是正的，我们不能同时分别增加和减少权重，而只能同时增加或减少所有的权重。

2.2 Tanh

深度学习中另一个非常常见的激活函数是 Tanh 函数。正切双曲线如下图所示：

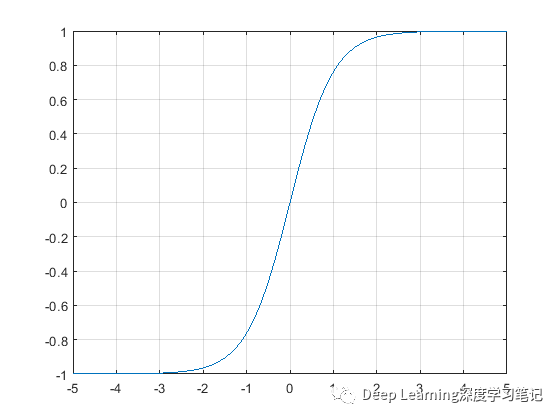
该函数根据以下公式将一个实值数映射到[-1, 1]范围：

与 Sigmoid 函数一样，神经元对两端大的负值和正值都会饱和，且函数的导数为 0 。但与 Sigmoid 函数不同，它的输出是以零为中心的。

因此，在实践中，tanh 非线性总是优于 Sigmoid 的非线性。

2.3 ReLU （Rectified Linear Unit）

ReLU 在过去几年变得非常流行。

对于大于零的输入，我们得到一个线性映射：

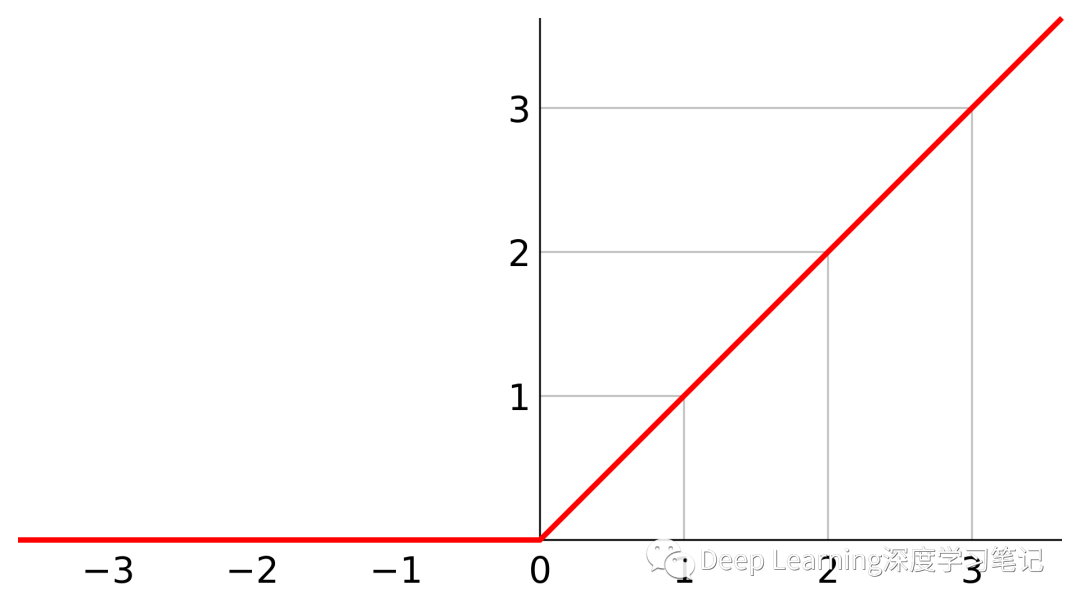
使用 ReLU 有几个优点和缺点：

优点：
- 实践证明，与其他激活函数相比，ReLU 加速了梯度下降向损失函数的全局最小值的收敛。这是因为它具有线性、非饱和的特性。
- 其他激活函数（Tanh 和 sigmoid ）涉及非常复杂的计算操作，如指数运算等，而 ReLU 则可以通过简单地将一个值向量的阈值设为零来轻松实现。
缺点：
- 因为对于低于零的输入值，这个函数的输出为零，这些网络神经元在训练过程中会非常脆弱，甚至会 "死亡"。这是什么意思呢？在权重更新过程中，权重的调整方式可能会导致某些神经元的输入值总是低于零，这种情况可能会发生（有可能性）。这意味着这些神经元的隐藏值始终为零，对训练过程没有贡献。这意味着流经这些 ReLU 神经元的梯度也将从这一点开始为零。我们说，这些神经元是无效的。例如，观察到整个使用 ReLU 激活的神经网络中多达 20-50% 的神经元可能是 "死 "的，这是非常常见的。或者换句话说，这些神经元在训练期间使用的整个数据集中永远不会激活。

2.4 Leaky ReLU

Leaky ReLu 是ReLU激活函数的一个改进版本。正如上一节所提到的，通过使用ReLU，可能会 "杀死 "神经网络中的一些神经元，这些神经元将永远不会再激活任何数据。Leaky ReLU是为了解决这个问题而定义的。与 ReLU相反，在 Leaky ReLU中，我们在函数中加入一个小的线性成分：

Leaky ReLU 如下所示:

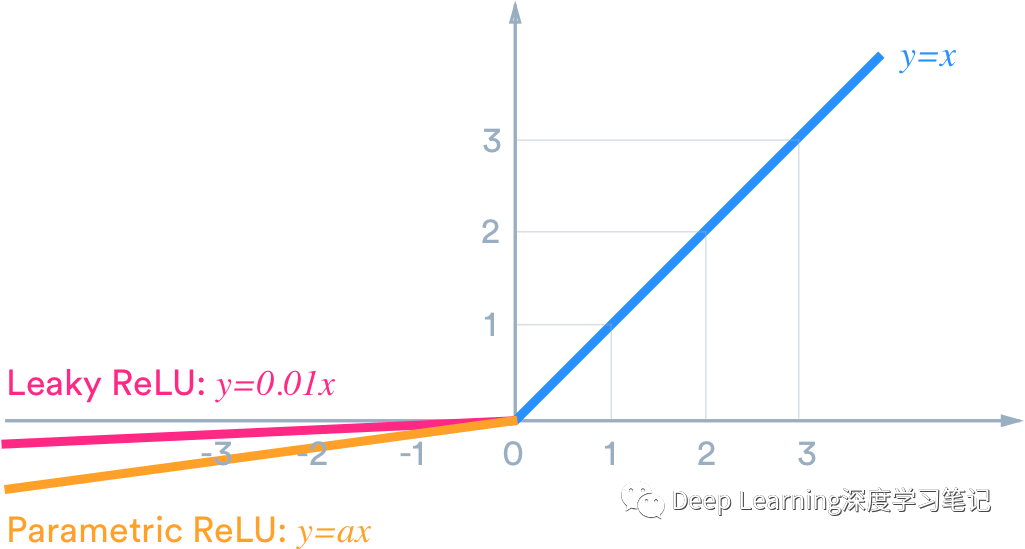
基本上，我们已经用一条非水平的线性线取代了低于零值的水平线。这条线性线的斜率可以通过与输入相乘的参数 (通常取 )来调整。使用 Leaky ReLU 并替换 ReLU 的优点是我们避免了零梯度。因为在这种情况下，我们不再有总是为零的“死”神经元导致我们的梯度变为零

2.5 Softmax

同样重要的是 Softmax 激活函数。这个激活函数是非常独特的。

Softmax 只在最后一层应用，而且只有当我们希望神经网络在分类任务中预测概率分数时才会用到

简单地说，softmax 激活函数输出神经元的值在 0 和 1 之间取值，因此它们可以代表概率分数。还有一点，我们必须考虑的是，当我们将输入的特征分类到不同的类时，这些类是相互排斥的。这意味着，每个特征向量只属于一个类别。在互斥类的情况下，所有输出神经元的概率分数总和必须为 1。只有这样，神经网络才能代表一个合理的概率分布。

Softmax 函数不仅强制输出到 0 和 1 之间的范围，而且该函数还确保所有可能的类的输出之和为 1 。

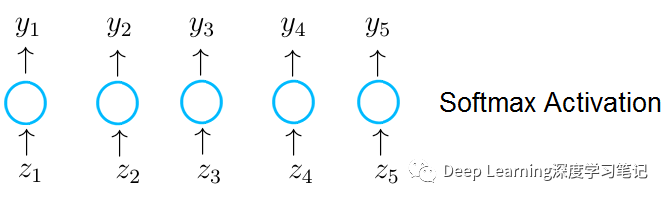
当我们使用 Softmax 时，输出层中神经元的每个输出都根据以下等式计算：

正如所看到的，一个特定的神经元的每个值不仅取决于神经元收到的值，而且取决于向量中的所有值。这使得输出神经元的每个值y都是 0 和 1 之间的概率值。这样一来，输出神经元现在代表了互斥类标签的概率分布。

2.6 ELU

ELU 也是 ReLU 的一种衍生版本：

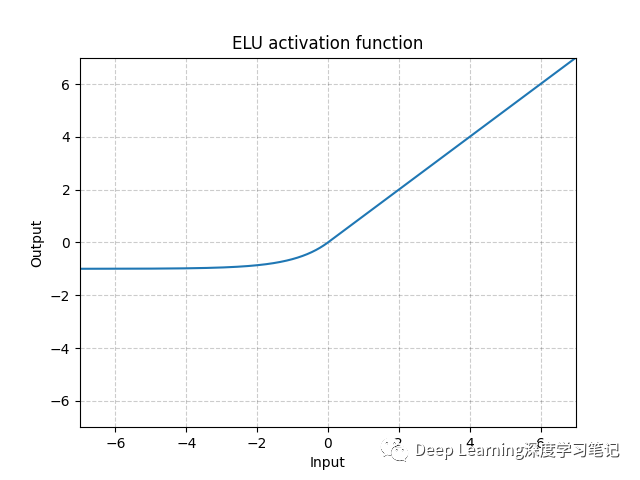
ELU 已被证明比 ReLU 产生更准确的结果，而且收敛速度也更快。ELU 和 ReLU 对于正的输入是一样的，但是对于负的输入，ELU 平滑得很慢，而 ReLU 迅速变为 0 :

值得注意的是常数必须是正数。 相比 ReLU，ELU 可以取到负值，这让单元激活均值可以更接近 0 ，类似于 Batch Normalization 的效果但是只需要更低的计算复杂度。虽然 Leaky ReLU 也有负值，但是它不保证在不激活状态下（就是在输入为负的状态下）对噪声鲁棒。反观 ELU 在输入取较小值时具有软饱和的特性，提升了对噪声的鲁棒性。

3. 选择激活函数

具体来说，这取决于要解决的问题和你所期望的输出值范围。如果你想让你的神经网络预测大于1的值，那么 Tanh 或 Sigmoid 就不适合用在输出层，我们必须用 ReLU 代替。另一方面，如果我们希望输出值在或范围内，那么 ReLU 就不是输出层的好选择，我们必须使用 Sigmoid 或 Tanh。如果执行分类任务，并希望神经网络预测互斥类标签的概率分布，那么在最后一层应该使用 Softmax 激活函数。然而，关于隐层，作为经验法则，一般来说默认使用 ReLU 作为这些层的激活。

参考资料

Activation function - Wikipedia
线性整流函数- 维基百科，自由的百科全书
双曲函数- 维基百科，自由的百科全书
Sigmoid function - Wikipedia
Activation Functions : Sigmoid, tanh, ReLU, Leaky ReLU, PReLU, ELU, Threshold ReLU and Softmax basics for Neural Networks and Deep Learning | by Himanshu S | Medium
Softmax function - Wikipedia