神经网络中必知必会的 5 个激活函数!
通用近似定理意味着神经网络可以近似任何将输入(X)映射到输出(y)的连续函数。表示任何函数的能力使得神经网络如此强大和广泛使用。
为了能够近似任何函数,我们需要非线性。这就是激活功能发挥作用的地方。它们用于向神经网络添加非线性。如果没有激活函数,神经网络可以被视为线性模型的集合。
神经网络是包含多个节点的图层。以下表示没有激活函数的节点。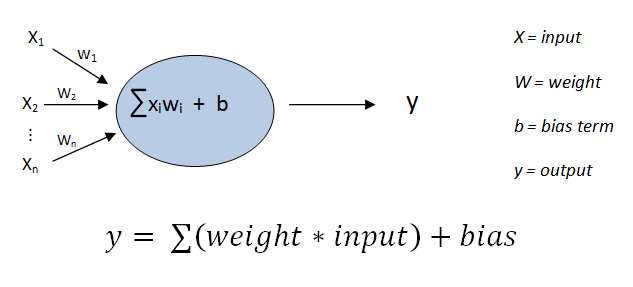 输出 y 是输入和偏置的线性组合。我们需要以某种方式添加非线性元素。请看以下节点结构。
输出 y 是输入和偏置的线性组合。我们需要以某种方式添加非线性元素。请看以下节点结构。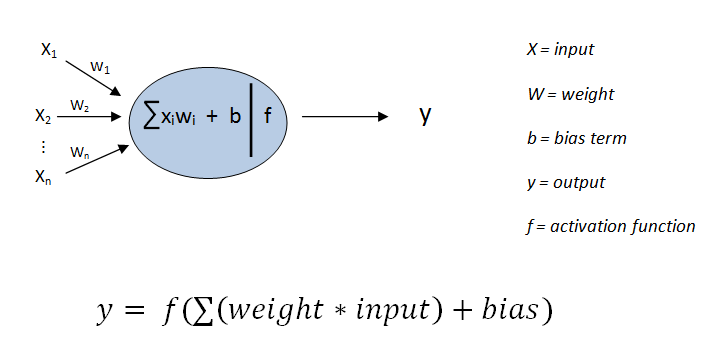 非线性是通过将激活函数应用于输入和偏置的线性组合的总和实现的。添加的非线性取决于激活函数。
非线性是通过将激活函数应用于输入和偏置的线性组合的总和实现的。添加的非线性取决于激活函数。
在这篇文章中,我们将讨论神经网络中5个常用的激活。
1、sigmoid
sigmoid 函数将值范围绑定到 0 和 1 之间。它还用于逻辑回归模型。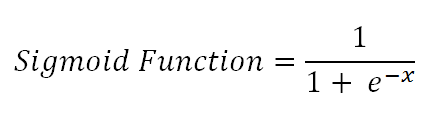 无论 sigmoid 函数的输入值是什么,输出值都将介于 0 和 1 之间。因此,每个神经元的输出被规范化到范围0~1。
无论 sigmoid 函数的输入值是什么,输出值都将介于 0 和 1 之间。因此,每个神经元的输出被规范化到范围0~1。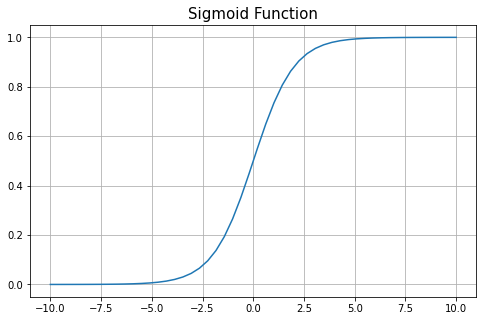 输出(y)对接近0的x值的输入(x)上的更改更敏感。当输入值远离零时,输出值变得不那么敏感。过了一点,即使输入值发生较大变化,输出值也很少或没有变化。这就是 sigmoid 函数实现非线性的方式。
输出(y)对接近0的x值的输入(x)上的更改更敏感。当输入值远离零时,输出值变得不那么敏感。过了一点,即使输入值发生较大变化,输出值也很少或没有变化。这就是 sigmoid 函数实现非线性的方式。
与此非线性相关的缺点,让我们先看看 sigmoid 函数的导数。
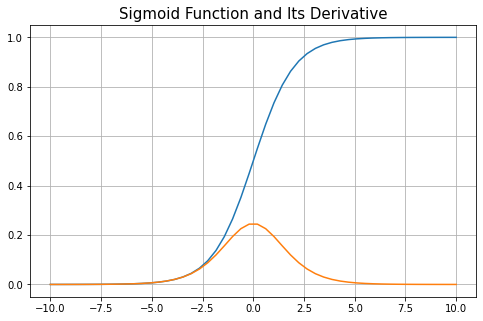
当我们远离零时,导数趋于零。神经网络的"学习"过程依赖于导数,因为权重是根据梯度进行更新的,梯度基本上是函数的派生。如果渐变非常接近零,则权重会以非常小的增量进行更新。这会导致神经网络学习速度如此之慢,需要很久才能收敛。这也称为「梯度消失问题」。
2、Tanh
它非常类似于 sigmoid,只不过输出值在 -1 到 +1 的范围内。因此,tanh 据说为零居中。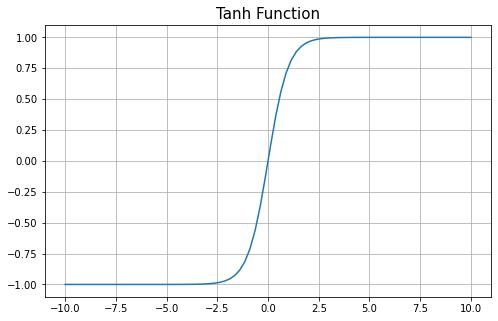 sigmoid 和 tanh 之间的区别在于,梯度不限于向一个方向移动。因此,tanh 的收敛速度可能快于 sigmoid 函数。
sigmoid 和 tanh 之间的区别在于,梯度不限于向一个方向移动。因此,tanh 的收敛速度可能快于 sigmoid 函数。
对于 tanh 激活功能,也存在消失的梯度问题。
3、ReLU
relu 函数只对正值感兴趣。它使输入值保持大于 0。所有小于零的输入值都变为 0。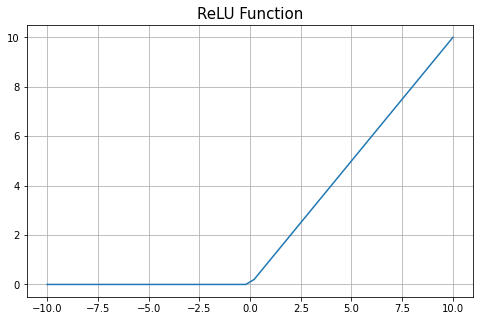
神经元的输出值可以排列为小于 0。如果我们将 relu 函数应用于该神经元的输出,则从该神经元返回的所有值都变为 0。因此,relu 允许取消一些神经元。
relu 收敛的速度比 tanh 和 sigmoid 快。
对于小于 0 的输入值,relu 的导数为 0。对于这些值,权重在回传期间永远不会更新,因此神经网络无法学习。此问题称为神经元死亡问题。
4、Leaky ReLU
它可以被认为是解决ReLU神经元死亡问题的办法。Leaky ReLU 输出负输入的小值。
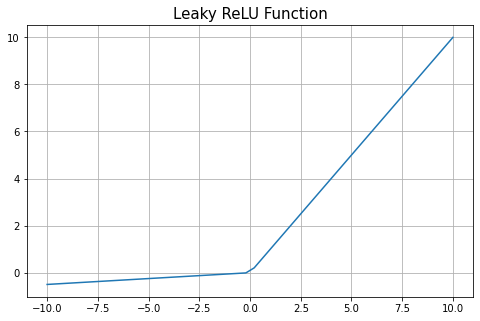
5、Softmax
Softmax 通常用于多类分类任务,并应用于输出神经元。它所做的是将输出值规范化为概率分布,使概率值加起来为 1。
Softmax 函数将每个输出的指数除以所有输出的指数之和。结果值形成概率分布,概率加起来为1。
让我们做一个例子。考虑目标变量有 4 个类的情况。以下是 5 个不同数据点的神经网络输出。
 我们可以将 softmax 函数应用于这些输出,如下所示
我们可以将 softmax 函数应用于这些输出,如下所示 在第一行中,我们将 softmax 函数应用于矩阵 A 中的值。第二行将浮点精度降低到 2 个小数。
在第一行中,我们将 softmax 函数应用于矩阵 A 中的值。第二行将浮点精度降低到 2 个小数。
下面是 softmax 函数的输出。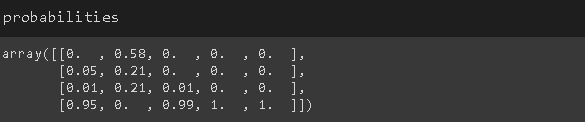

推荐一本由美国科学作家 Michael Nielsen编写的非常好的深度学习入门书籍-《Neural Network and Deep Learning》,中文译为《神经网络与深度学习》。
个人认为是目前最好的神经网络与机器学习入门资料。内容非常浅显易懂,很多数学密集的区域作者都有提示。全书贯穿的是 MNIST 手写数字的识别问题,每个模型和改进都有详细注释的代码。非常适合用来入门神经网络和深度学习!

领取方式:
长按扫码,发消息 [神经网络]
