终于有人把线性回归讲明白了

来源：大数据DT

本文约1900字，建议阅读5分钟 
本文将介绍什么是回归问题、解决回归问题的基本思路步骤和用机器学习模型解决回归问题的基本原理，以及如何用线性模型解决回归问题。

本文将介绍机器学习算法，我们选择从线性回归（Linear Regression）开始。

许多机器学习教材习惯一上来就深入算法的细节，这当然也有好处，但学习一门之前不大接触的新技术时，我更倾向于遵循学习思维三部曲的节奏：是什么（What）、为什么（Why）和怎么做（How）。如果我们之前未接触过机器学习，那么开始学习时首先问的当然是“机器学习是什么”。

所以我们选择从线性回归算法开始。线性回归算法不但结构简单，原理好懂，同时又包含了机器学习算法的典型运作特征，方便你鸟瞰机器学习算法的运行全貌，以及仔细观察每个组成构件的细节情况。如果此前你并不了解机器学习，不妨将线性回归当作机器学习算法中的入门任务。

学习新技术一直存在这样的矛盾：技术太复杂则担心学不会，技术太简单又担心是不是已经过时了。毕竟我们这个时代的计算机科学正在一日千里地飞速发展着，计算机类教材里的许多技术可能已经被新兴技术取代而退出了历史舞台，只是出于知识结构的完整性等考虑才像恐龙骨架一样在教材里保留着一席之地。

但请放心，线性回归完全不是这么一回事。线性回归是一套在当下仍然具有很高实战价值的算法，在很多现实场景中仍然发挥着不可替代的作用，不但“麻雀虽小，五脏俱全”，适合介绍剖析，而且还像麻雀一样，蹦蹦跳跳地活跃在机器学习应用的第一线。

想要说清楚线性回归，先回到“线性回归”这个吓人的名字上。在通往机器学习的路上有着各色各样的拦路虎，首先跳出来吓你一哆嗦的肯定是那些古古怪怪的术语，“线性回归”就是里面的杰出代表。

初次接触“线性回归”，可能都不知道该怎么断句，一不小心就要被吓得干脆打退堂鼓。不要怕它，首先我们将这个看似无从下手的词分成“线性”和“回归”两块，可以认为这代表了两个知识领域：前者是一类模型，叫“线性模型”；后者是一类问题，叫“回归问题”。这样“线性回归”这个词可以理解成一句话，即用线性模型来解决回归问题。

线性模型和回归问题凑成一对并非是剧本一开始就安排好的。回归问题是机器学习中非常经典的一类问题，换句话说，就是有许许多多的方法模型都会用于解决回归问题。但除了回归问题，这些方法模型也可以解决其他问题，如分类问题。

总而言之，问题和模型是多对多的关系，问题提出要求，模型给予解决，毕竟算法和人生一样，没有剧本只有惊喜，遇上了又能对得上，那才好凑成一对，所以当大家用线性模型解决回归问题时发现还挺顺手并经常用，后来干脆起了“线性回归”这个名字。

介绍完了名字，接下来就是“正菜”。大多数教材最习惯的做法是一上来就抛出各种眼花缭乱的公式，让人深深陷入术语、符号和推导等细节之中，就像是正要开始学游泳，不知就里便被扔进了大海，从此拖着长长的心理阴影。

细节很重要，但理念更重要，刚接触机器学习谁都只是一张白纸，要在上面大展宏图，首先得确定基本主题，然后勾勒整体脉络，最后才是添加细节。这也正是本书介绍机器学习的方式。

机器学习是问题导向的，正因有了问题才会设计算法，这是机器学习最主要的脉络。本文要解决的问题是回归问题，用的方法是线性回归算法。如果也将线性回归算法比作一架机器，那线性方程和偏差度量就是组成这架机器的两大构件，它们在权值更新这套机制下齐心协力地运转，最终解决回归问题。

这也是本文的要点，请格外加以关注：

• 回归问题

• 线性方程

• 偏差度量

• 权值更新

01 用于预测未来的回归问题

所以如果你担心接下来将要看到什么深奥的术语则大可不必，机器学习并非凭空而生的学科，这里所说的回归问题正是从统计学那里借来的救兵。

两百年前，与达尔文同时代的统计学家高尔顿在研究父代与子代的身高关系时，发现一种“趋中效应”：如果父代身高高于平均值，则子代具有更高概率比他父亲要矮，简单来说就是身高回归平均值。“回归”一词也由此而来。

在回归的世界里，万物的发展轨迹都不是一条单调向上走或向下走的直线，而是循着均值来回波动，一时会坠入低谷，但也会迎来春暖花开，而一时春风得意，也早晚会遇到坎坷挫折，峰回路转，否极泰来，从这个角度看，回归与其说是一个统计学问题，不如说更像是一个哲学问题。

那么什么是回归问题呢？回归问题的具体例子很多，简单来说各个数据点都沿着一条主轴来回波动的问题都算是回归问题。

回归问题中有许多非常接地气的问题，譬如根据历史气象记录预测明天的温度、根据历史行情预测明天股票的走势、根据历史记录预测某篇文章的点击率等都是回归问题。正因为回归问题充满了浓厚的生活气息，也就成为一类十分常见的机器学习问题。

当然，回归问题作为一种类型，有着自己独特的结构特征，在上面描述什么是回归问题时，我刻意反复使用“历史”和“预测”这两个词，原因正是记录历史值和预测未来值是回归问题的两个代表性特征。

在机器学习中，回归问题和分类问题都同属有监督学习，在数据形式上也都十分相似，那么怎么区分一个问题究竟是回归问题还是分类问题呢？

• 回归问题和分类问题最大的区别在于预测结果

根据预测值类型的不同，预测结果可以分为两种，一种是连续的，另一种是离散的，结果是连续的就是预测问题。

这里的“连续”不是一个简单的形容词，而是有着严格的数学定义。不过额外引入太多复杂的概念反而会偏离主线，好在“连续”是一个可以感受的概念，最直接的例子就是时间，时间当然是连续的，连续型数值在编程时通常用int和float类型来表示，包括线性连续和非线性连续两种，如图3-1所示。

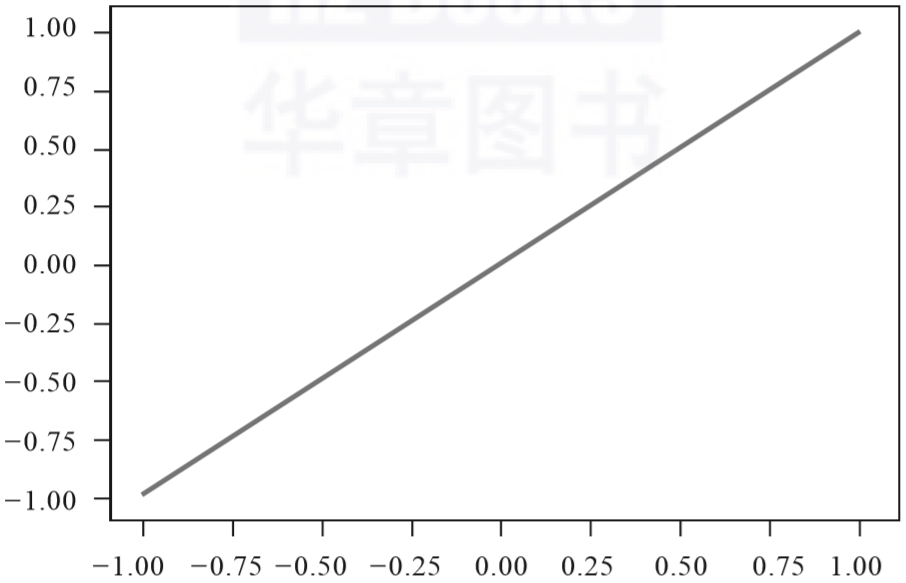
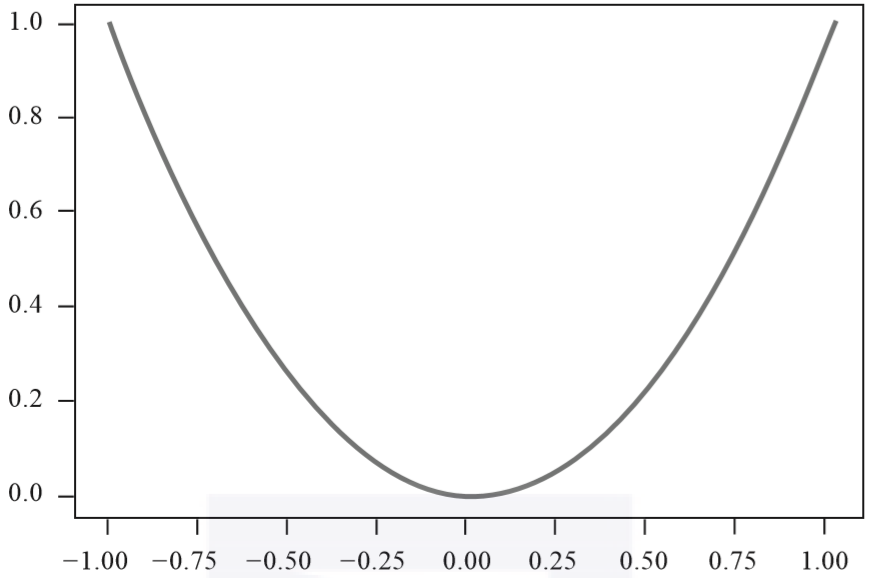
相比之下，离散型数值的最大特征是缺乏中间过渡值，所以总会出现“阶跃”的现象，譬如“是”和“否”，通常用bool类型来表示，如图3-2所示。

▲图3-2 离散型数据

02 怎样预测未来

回归问题是一类预测连续值的问题，而能满足这样要求的数学模型称作回归模型，我们即将介绍的线性回归就是回归模型中的一种。许多教材讲到回归模型，总是匆匆进入具体的算法当中，而往往忽略替初学者解答一个问题：为什么回归模型能够进行预测？这是一个似乎理所当然，但其实并没有那么不喻自明的问题。

许多人对“预测”的第一印象也许是传说中的一个故事，有两位高人结伴出行，晚上歇于一处破庙，甲对乙说，“睡觉别靠墙，我刚掐指一算，寅时墙会倒。”乙不屑一顾地摆摆手，“我刚才也掐指一算，墙是倒向右边，我靠左睡可保无忧。”

故事里的高人也是要看书的，不过多半看的是《奇门遁甲》，而不太可能是《机器学习》。奇门遁甲不在本书的讨论范围，那么，机器学习的回归模型能不能实现精准的预测呢？

也许可以，不过要有条件：需要有充足的历史数据。数据的重要性怎么强调都不为过，如果将机器学习算法比作一架机器，那么数据就是驱动这架机器的燃料，没有燃料驱动，机器设计得再精巧也只能是摆设。

我们不是要预测未来吗，为什么反而说历史数据这么重要呢？这个问题涉及哲学，可以追溯到世界是万事万物相互联系的统一整体，或者简单一点，不妨把预测当作一次侦探小说中的推理过程，犯罪手法总是要留下痕迹的，只要你找到相关联的线索，就能够推理出最终的结果。

当然，预测难就难在待预测对象与什么相关是未知的，不过好在其中的关联关系就藏在历史数据之中，你要做的就是通过机器学习算法把它挖掘出来。机器学习算法并不发明关系，只是关联关系的搬运工。有一种尚存争议的观点甚至说得更直白：机器学习远不是什么欲说还休的神秘技术，从数学的角度看就是拟合，对输入数据点的拟合。

• 机器学习实现预测的流程

机器学习算法究竟有什么魔力，竟然能够预测未来？不妨就以前面两个高人的故事为例，用科学观点来研究墙体坍塌的问题。墙体坍塌可能由许多偶然因素导致，我们都不是土木专家，不妨凭感觉随手列出几条可能导致墙坍塌的因素：

• 譬如可能与砌墙的材质有关，土坯墙总比水泥墙容易垮塌；

• 可能与使用时间的长短有关；

• 可能与承建商有关，喜欢偷工减料的工程队容易出“豆腐渣工程”；

• 还有一些外部环境因素，譬如整天风吹雨淋的墙容易垮塌；

• 最后就是墙体坍塌之前总会有一些早期迹象，譬如已经出现很多裂缝等。

上面所列因素有三种情况：与坍塌密切相关，与坍塌有点关系，以及与坍塌毫无瓜葛。如果人工完成预测任务，当然最重要的工作就是找出哪些是密切相关的，放在第一位；哪些是有点关系的，放在参考位置；哪些毫无瓜葛，统统删掉。

可是我们又怎么知道哪些因素有哪些关系呢？这时我们就可以制作一张调查表，把砌墙用的什么材料、已经用了多久、出现了多少条裂缝等情况一一填进去，这就是前面所说的数据集中每一条样本数据的维度。就像商家很喜欢通过网上问卷来了解用户偏好一样，我们也利用调查表来了解墙体坍塌有什么“偏好”。

调查表大概形式如下表所示。

最后一栏是“坍塌概率”，这是我们最关心的，也是有监督学习所必需的。这些已知的坍塌概率以及相关的维度数据将为未知概率的预测提供重要帮助。

最后也是最关键的一步，是找出各个维度和坍塌之间的概率，而这个步骤将由模型自行完成。

我们要做的只是将长长的历史数据输入回归模型，回归模型就会通过统计方法寻找墙体坍塌的关联关系，看看使用时间的长短和承建商的选择谁更重要，相关术语叫作训练模型，从数学的角度看，这个过程就是通过调节模型参数从而拟合数据。怎样调节参数来拟合数据是每一款机器学习模型都需要思考的重要问题。

模型训练完毕后，再把当前要预测的墙体情况按数据维度依次填好，回归模型就能告诉我们当前墙体坍塌概率的预测结果了。流程如图3-3所示。

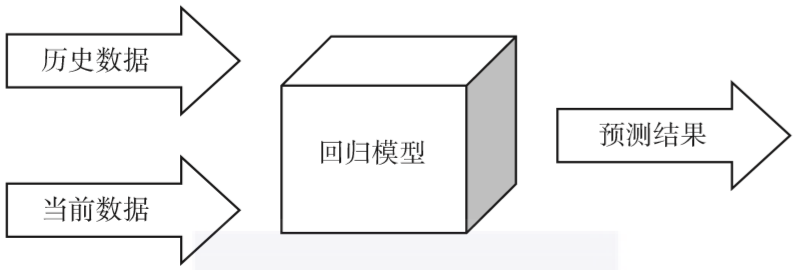
▲图3-3 回归模型训练示意图

可以看出，回归模型就是预测的关键，我们通过给模型“喂”数据来训练它，最终让它具备了预测的能力。也许你对“模型”这个词感到陌生又好奇，不知道该在脑海里给它分配一个什么样的形象。而图3-3的“模型”是一个大大的四方盒子，塞进数据就能吐出预测结果，像是奇幻故事中巫师手中具有神奇魔力的水晶球。

不用着急，“模型”这个词将贯穿我们对机器学习的整个巡礼，就像庆典游行里的花车正等着我们逐一观赏呢。接下来迎面走来的就是第一款模型——线性模型。

03 线性方程的“直男”本性

也许你对名为“模型”的大盒子充满期待，同时又担心会冒出一大堆数学符号，所以不敢马上掀开一窥究竟。不过，线性模型反倒更像是一个过度包装的大礼盒，大大的盒子打开一看，里面孤零零只有一样东西：线性方程。第一次接触时各种名词很容易把人绕糊涂，不急，我们先把名词之间的关系捋一捋。

前面在介绍机器学习的基本原理时，提到“假设函数”这个术语，假设函数是一类函数，所起的作用就是预测，这里的线性方程就是线性回归模型的假设函数。

别看名字挺“高冷”，其实特别简单。“线性”就是“像直线那样”，譬如线性增长就是像直线那样增长。我们知道，直线是最简单的几何图形，而线性方程说直白一点，就是能画出直线的一种方程。如果方程有性格的话，那么线性方程一定就是“直男”的典型代表。

直线方程最大的特点就是“耿直”，由始至终都是直来直去，函数图像如图3-4所示。

▲图3-4 线性函数的函数图像

这样看好像也没什么，但对比一下同样常见的以2为底数的对数函数（见图3-5a）和指数函数（见图3-5b）就能明显看出，其他函数多多少少都要带一点弧度，这是变化不均匀所导致的。相比之下，直线方程开始是什么样子则始终是什么样子。

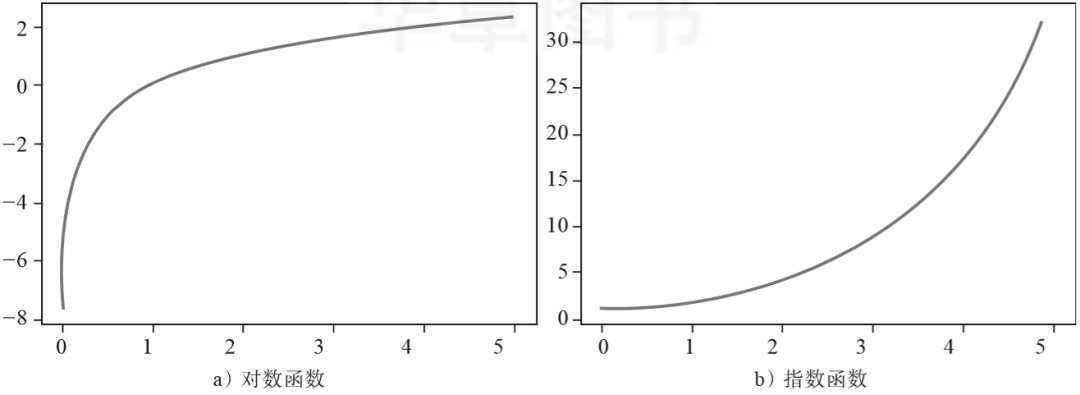
▲图3-5 非线性函数的函数图像

直线方程通常写作y=kx+b，k称为斜率，b称为截距，这两个参数可以看作两枚重要的旋钮，直接控制直线进行“旋转”和“平移”的动作。具体来说，通过调整斜率，可以改变直线的角度。

在图3-6的四幅图中，直线均具有相同的截距，黑实线斜率均为2，但右上、左下、右下的三幅图中灰线斜率分别为1、1/2和0，对比黑实线可以看出，通过改变斜率可以使直线出现“旋转”的动作效果。

▲图3-6 4条斜率不同的线性函数图像对比

直线还有另一种调节方法。通过调整截距b，可以实现直线的上下平移。如图3-7所示，这三条平行的直线具有相同的斜率，但截距相差1，可以看到直线出现了上下平移的动作效果。

“旋转”和“平移”就是直线的全部看家本领了，这正体现了线性方程简单直率的“直男”本性。

准确来说，线性方程和直线方程还是存在一点微小差别的。直线是二维平面图形，而线性所在的空间则可能是多维的。不过，无论是在二维平面还是在多维空间，直线所能做的也就是“旋转”和“平移”两套动作，线性模型想要拟合能够调节的参数，主要也就只有这两个。

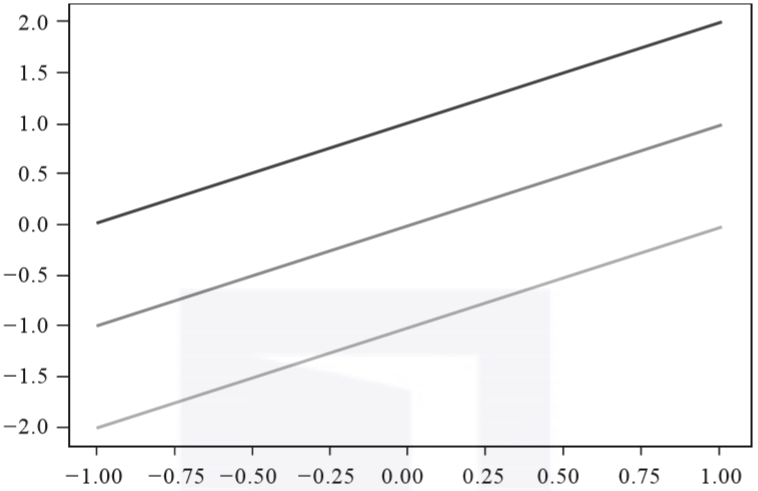
▲图3-7 三条截距相差1的线性函数图像对比

在机器学习中，斜率k通常用字母w表示，是权值（weight）的首字母。通过调整w和b的值就能控制直线在多维空间中进行旋转和平移，扮演的角色很像老式收音机上的旋钮，通过旋转旋钮就可能收听到想要的电台。

这个通过调整权值来达到目的的过程叫作权值调整或者权值更新，对于线性模型而言，学习过程的主要工作就是权值调整，只要旋动旋钮，合理搭配旋转和平移这两套简单的动作，就能完成对输入数据的拟合工作，从而解决回归问题。

• 关于调整权值的另一种解释

在机器学习中，通过调整权值来完成学习，并最终进行预测的算法很多，这也是一种非常常见的学习手段。对于为什么调整权值能够进行预测，实际上也有多种解释，上面从几何角度给出了解释，此外还有代数角度的解释。

以三个输入维度A、B、C来预测P为例，我们的线性方程可以写为：

F=W1*A+W2*B+W3*C

假设我们知道P的值其实就是与A的值有关，与B、C毫无关系，那么，怎样调整线性方程才可以根据输入准确预测出P的值呢？

我们知道，线性方程的计算结果F是三个维度的加权和，想要使F与P最接近，只需要让线性方程中B、C这两个加项对结果影响最小即可。这个好办，只要使这两项的权值最小，也就是W2和W3的值为0就可以了。

这就是从代数角度来解释为什么调整权值能够提高预测结果的准确性。这里实际上体现了一种假设，就是待预测的结果与输入的某个或某几个维度相关，而调整权值的目的就是使得与预测结果相关度高的权值越高，确保相关维度的值对最终加权和的贡献越大，反之权值越低，贡献越小。

04 最简单的回归问题——线性回归问题

前面我们介绍了什么是回归问题，也直观感受了线性方程的“直男”本性，那么在这一节将对为什么模型能进行预测给出一个很直接的回答。当然，学术界对于这个问题的认识还未完全统一，这里选择沿用一种当前最主流的观点。

直到目前为止，我们还不能全面地了解这个世界，但纷繁复杂的现实世界大体还是遵循着某种规律的，我们不妨叫作“神秘方程”。而我们在机器学习领域所做的，就是通过历史数据训练模型，希望能够使我们的模型最大限度地去拟合“神秘方程”——一旦偷看了导演的剧本，还怕有什么剧情不能预测吗？

不过，也许你已经发现，这存在一个问题。

就拿线性模型来说吧，线性模型是用直线方程去拟合数据，但直线可是“钢铁直男”，它的动作也只有两套而已啊！模型的能力是有上限的，能力跟不上，想最大限度地拟合也还是心有余而力不足。

所以，选择模型的关键不在于模型的复杂程度，而在于数据分布。你也许会担心，线性模型简单好懂，这也是它为什么特别适合用来做入门任务，但唯一的问题是它太简单了，现实世界这么复杂，它真的能够解决问题吗？

要知道尺有所短，寸有所长，回归问题是一个大类，其中有一类问题叫线性回归问题，遇到这种问题不用线性模型还真就不行。下面，我们就来看看线性回归是怎样完成预测的。

• 利用线性回归进行预测的极速入门

在线性回归问题里，所要预测的“神秘方程”当然也是线性方程。这类方程存在固有特征，最明显的就是数据集点沿线性分布，所以用线性模型效果最好。也许你不敢相信，这个世界这么复杂，真的有这么简单的“神秘方程”吗？真的有，而且你肯定还见过，一起来回忆一下：

已知小明前年3岁，去年4岁，今年5岁，请问小明明年几岁？

首先这无疑是个预测连续值的问题，明明白白是一个回归问题。回归关注的是几个变量之间的相互变化关系，如果这种关系是线性的，那么这就是一个线性回归问题，适合用线性模型解决。我们按照机器学习的习惯，把已知条件整理成数据集，这是一个三行两列的矩阵：

[[2017，3],

[2018，4],

[2019，5]]

这是一个二维矩阵，如果画出图像，两个维度之间的线性关系就一目了然。这里以年份为X轴、年龄为Y轴将记录的数据画出来，得到3个呈线性排列的数据点（见图3-8a）。把这些点用线段连接起来，就能更清楚地看到这3个点排成了一条直线（见图3-8b）。

这条直线写成线性方程就是y=x-2014，即所谓的“假设函数”。线性回归的预测就依赖于这条方程，2019年刚刚过去，我们当然只能知道2019年之前的真实数据，但对于未来也就是小明在2019年之后的年龄，通过这条线性方程即可以预测得到。

譬如把“2020”作为x输入，就能计算出对应的y值是“6”，也就得到了2020年小明将是6岁的预测结果。这个例子很简单，但已经完整地展示了线性回归“预测魔力”背后的原理，线性回归的预测魔力还经常被运用在经济和金融等场景，听起来更高端，不过就原理来说，也只是这个简单例子的延伸和拓展。

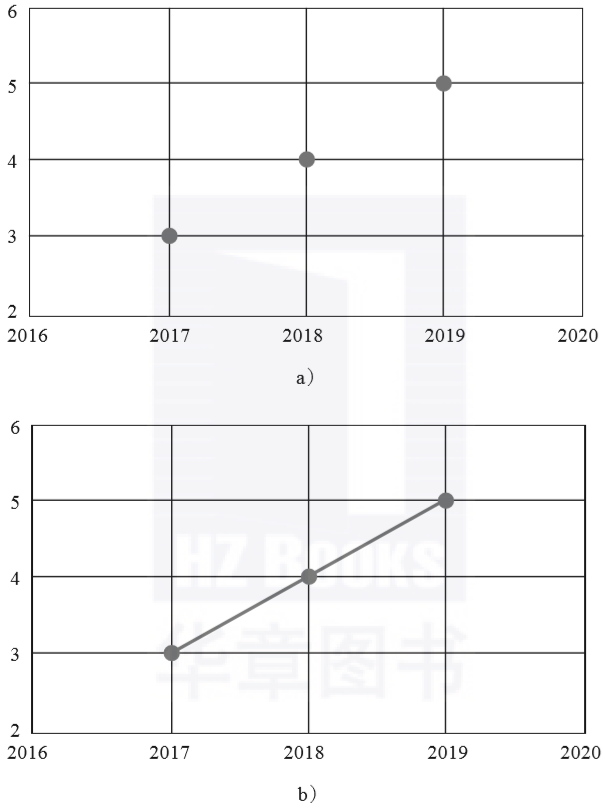
▲图3-8 呈线性关系的数据集点分布（a），如果连起来会出现一条直线（b）