小朋友都能懂的计算机算法 - 加解密
电话手表
小明最近很开心,
妈妈给他买了一块电话手表。
他的好朋友小辉早就有电话手表了。
小明在科学课上觉得有点无聊,
就悄悄用电话手表给小辉发消息,
二人你来我往,
上课又开始变得有意思了。
小明放学回家,
妈妈一脸严肃的说:
辣条好吃吗?
小明被问了个措手不及:
我,他,你,那个,这个…. 没有啊!
小明心里想,
不应该啊,
难道发消息还被监控了?
又大又坏的网络世界
小明以为他和小辉之间发消息是这样的:

实际发消息的过程是这样的,
实际上还要复杂的多:
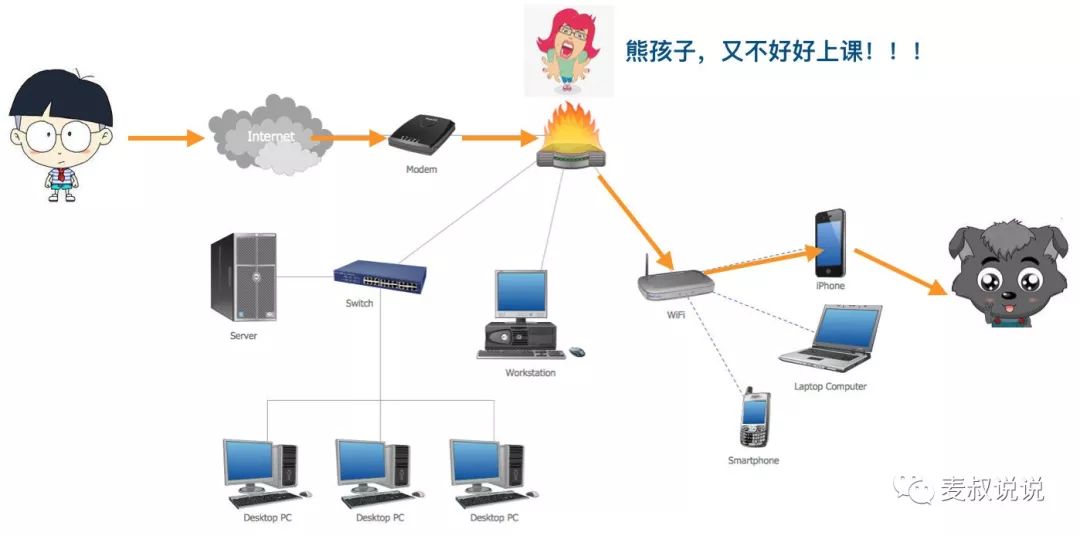
这个“买辣条”的重大消息,
中间经过了数十上百个节点的中转,
最后才到达小辉的手机上。
这其中的每一个中转节点都能看到这条消息,
而恰好其中一个中转节点是电话手表厂的,
而电话手表厂悄悄的把消息转给了妈妈。
还好是妈妈,
都是为了你好!
但这是一个又大又坏的网络世界,
网络上有无数的坏的中转节点,
随时想要截获你的消息,
比如银行密码,
比如支付宝账号等等。
那该怎么办呢?
这可是至关重要的,
现在我们每天都离不开网络了。
所以不管你是不是计算机行业的,
不管你是大朋友还是小朋友,
都应该学习一点密码学知识,
增强自己的防骗能力。
这些密码学知识看似高深,
其实都来源于生活,
也很容易懂。
传纸条
小明和小辉知道了电话手表通话并不安全,
于是他们决定用新办法 - 传纸条!
这次他们要讨论一下周六几点去买辣条。
但是这个时间不能被其他同学知道,
否则他们可能会来抢辣条,
总之不能让他们知道几点去买!

但传纸条的过程必须要经过其他同学。
于是他们决定给纸条的内容加密!
纸条上就写着一个数字,

这表示18点去买辣条。
但如果就这么把纸条传过去,
必然被其他同学知道,
到时候他们来抢辣条就不好了!
于是他们决定给数字加密,
加密方法很简单,
就是给这个数字加上小明的年龄11,
那么纸条上的数字不再是18,
而成了29。
18 + 11 = 29
小明在纸条上写了29:

小辉看到以后把29减去11就得到了18。
29 - 11 = 18
而其他同学并不知道需要减去11,
所以不知道29是什么意思,
也猜不出小明他们是18点去买辣条。
对称加密
这就是最简单的加密算法。
因为这种算法加密和解密过程都要用到同一个数字,
这种算法被称为对称加密算法,
这个用来加解密的数字被称为秘钥,
要发送的内容(18)被称为明文,
加密后的内容(29)被称为密文。
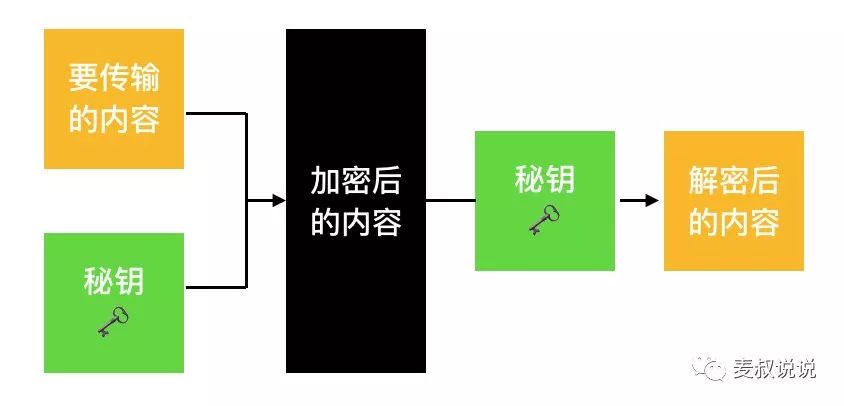
这个过程很简单:
发送者把明文使用秘钥加密成密文
接受者通过同一个秘钥把密文再转成明文
这个过程很简单,
但有个关键点:
小明和小辉必须都知道这个秘钥11,
而其他同学必须不知道这个秘钥
否则这个加密就没用了。
不要小看这个对称加密算法,
这个算法现在使用极其广泛,
你几乎每天都在使用!
虽然真正使用的秘钥和算法不会像11这么简单,
但思路和道理是完全一样的。
这些复杂的对称算法中最出名的叫做AES,
英文名是Advanced Encryption Standard,
中文名是高级加密标准。
这个算法的秘钥可不是简单的11,
而是一个128,192或者256位的二进制数字,
它的算法也不是简单的加上秘钥,
而是先把明文分割成一个个小块,
再对这些块经过10或者14道各种运算最后才得到密文,
这个密文可以用同一个秘钥再计算出明文。
中间的网络节点拿到的数据是完全混乱的,
在不知道秘钥的情况下如果想要破解明文,
需要多长时间呢?
我们来算一下:
假设秘钥长度是256,
它的组合一共有2的256次方,
这个数字大的超出你想象!
转换成10进制以后是:

也就是说要猜出秘钥需要尝试这么多次,
就算用超级计算机,
每秒可以猜测20亿亿次,
都上猜上最少几十亿年的时间,
那时候太阳系都完蛋啦!
这么看AES是很安全的,
这个世界得救了!

等一等,还有一个很关键的问题没解决,
如果秘钥被人窃取了就没有安全可言了,
有秘钥的中间节点可以用秘钥轻松解密!
如何在发送者和接受者之间传递秘钥呢?
在计算机网络上,
没办法让两台电脑之间说悄悄话交换秘钥。
必须有一个方法,
可以让两者之间安全的传递秘钥,
而不被中间节点猜出来秘钥是什么!
怎么办?
两把钥匙
怎么解决传递秘钥的问题呢?
后来有了解决方法,
我们现在来玩一个游戏:
你在心里想一个3位数,
把这个3位数乘以91,
然后告诉我结果的后3位,
我就能算出你心里想的数字!
信不信?
我们来试一下:
假设你在心里想了365,
365 x 91 = 33215,
你把 215 告诉我。
从常规思路去看,
根本没办法从215猜出365来!
但是我能:
215 x 11 = 2365
你心里想的就是就是结果的后3位365!
是不是很神奇?
你可以心里多想几个3位数试试看!
哪里冒出来的11?
原理其实也简单,这是一个数学问题。
91 x 11 = 1001
任何1个3位数乘以1001得到的结果的后3位都是它自己, 因为1001的后3位是001, 任何1个3位数乘以1都是它自己!
我把1001分解成了 91 x 11 这两个数
我把 91 公开给了你,但是 11 自己秘密保留!
你把心里想的数字先乘以 91,告诉了我后3位, 只要后3位就够了,因为前面的位数不会影响后3位的值,
所以我用你给我的后 3 位再乘以 11 就相当于乘以了 1001
得到的结果的后 3 位就是你最初想的那个 3 位数字!
好神奇啊🤩!
在这里我有两把钥匙,
分别是 91和 11,
我把 91公开给所有人,
任何人想要发消息给我就按照上面的方法加密,
只有我才能用第二把秘密钥匙11算出你要发的消息,
别人就算看了我的小纸条也是不可能算出消息内容的!
用同样的方法,
我们可以构造出更大更复杂的钥匙对,
也不用局限于3位数,
比如我们可以用
19801 x 20201 = 400000001
构造出末8位都不会变的加密系统,
其中19801和20201构成一对钥匙!
这个方法有点类似于家门口的快递箱,
任何一个人都可以往箱子里塞入快递,
但是只有有钥匙的人可以打卡快递箱拿到快递!
区别是发送快递并没有用公开的钥匙加密。

这是一个伟大的发现,
这个方法现在应用非常广泛,
可以说是互联网加密的基石!
只不过具体实现比我们上面的例子要复杂的多,
它们可能不是用简单的乘法,
而是用更复杂的指数运算,取模运算等!
非对称加密
上面的加密方法有两把🗝,
第一把🗝用来加密,
而只有第二把🗝才能解密,
所以这种方法被称为非对称加密。
和前面的对称加密方法明显不同,
对称加密是同一把🗝用来加密和解密,
这个🗝决不能公开,
只有发送者和接受者知道!
而非对称加密有两把🗝,
第一把是公开的,
第二把也是绝对不能公开的,
一旦公开了别人就可以破解密文了。
非对称加密也被称为公钥加密,
因为它的重要性,
本文就用了公钥加密作为标题!
1976两位美国的科学家首先提出这个算法,
他们是Whitfield Diffie 和 Martin Hellman:

他们发明了Diffie-Hellman密钥交换算法。
1977年另外三位科学家,
Rivest、Shamir 和 Adleman,
用类似的原理发明了一种新的算法。

这种算法用他们3人的名字首字母命名,
叫做RSA算法,

他们还申请了专利,
谁要用这个算法都要给他们钱,
好在每个发明专利只有20年的有效期,
他们的专利在2000年已经失效,
现在地球人都可以免费的使用这个算法啦!
这两种算法都是公钥加密算法,
公钥加密算法使用非常广泛,
大家经常上的淘宝、京东都用了公钥加密,
这两年火起来的区块链技术更是基于公钥加密。
你懂了吗?
对称加密算法和非对称加密算法!
