通俗易懂之最小二乘法(附matlab和python例子实现)-技术圈

前言

最小二乘法也称最小平方法，是一种数学优化技术，通过最小化误差的平方和来寻找数据的最佳函数匹配。

感谢各友的鼓励与支持🌹🌹🌹，往期文章都在最后梳理出来了(●'◡'●)

👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇

线性函数模型

典型的一类函数模型是线性函数模型。最简单的线性式是y=b0x+b1写成矩阵形式为：

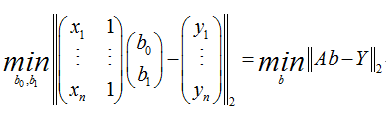
直接给出该式的参数解：

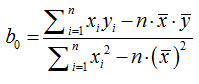
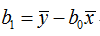
其中：

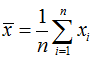
为x的算术平均值，也可解得如下形式：

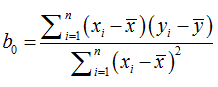
最小二乘法原理

假设结果y与m个因素x[i]有关，且为线性关系，即：

y = k[0] + k[1] * x[1] + k[2] * x[2] + ... + k[m] * x[m]

经过测量，现有n组数据(n >= m)，求合适的k[i]，使得上述表达式与测量结果尽可能的相符。

最小二乘法的做法很简单，让所有残差的平方和最小即可，设p[i]表示第i组测试数据，把k[i]看成未知数，最小化f：

f = (p[1] - y[1]) ^ 2 + (p[2] - y[2]) ^ 2 + ... + (p[n] - y[n]) ^ 2

实例分析

这里举个简单例子说明最小二乘法的过程。现要用钱去买游戏币，售币处贴出公示如下：

10元 —— 11个游戏币20元 —— 23个游戏币50元 —— 58个游戏币100元 —— 123个游戏币

显然，付的钱数与得到的游戏币存在某种线性关系，设有：y = ax + b，代入以上数据得：

 10a + b = 11 20a + b = 23 50a + b = 58100a + b = 123

构造残差函数

f = (10a + b - 11) ^ 2 + (20a + b - 23) ^ 2 + (50a + b - 58) ^ 2 + (100a + b - 123) ^ 2

分别对a, b求偏导，并令其等于0，才能使f取得最值。

20(10a + b - 11) + 40(20a + b - 23) + 100(50a + b - 58) + 200(100a + b - 123) = 0 2(10a + b - 11) +  2(20a + b - 23) +   2(50a + b - 58) +   2(100a + b - 123) = 0

解出结果：a = 1.2439, b = -2.2245，从而关系式为：y = 1.2439x - 2.2245。

有了该表达式，现在可以对未知点进行预测了，例如80块钱，大约可以买97个游戏币，而125元钱大约可以买153个。

python实现

import numpy as npfrom scipy.optimize import leastsq
def func(p, x):    k, b = p    return k * x + b
def error(p, x, y):    return func(p, x) - y
X = np.array([10, 20, 50, 100])Y = np.array([11, 23, 58, 123])P = (0, 0)
ret = leastsq(error, P, args=(X, Y))
k, b = ret[0]print(k, b)

运行结果：

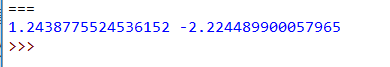
解出k=1.24388, b=-2.2245，与上面手算的一致。可以通过pyplot将数据以图的形式直观的展现出来。

import numpy as npfrom scipy.optimize import leastsqimport matplotlib.pyplot as plt
def func(p, x):    k, b = p    return k * x + b
def error(p, x, y):    return func(p, x) - y
X = np.array([10, 20, 50, 100])Y = np.array([11, 23, 58, 123])P = (0, 0)
ret = leastsq(error, P, args=(X, Y))
k, b = ret[0]print(k, b)

plt.figure()plt.scatter(X, Y, color='red')x = np.linspace(0, 200, 200)y = k * x + bplt.plot(x, y)plt.show()

运行结果：

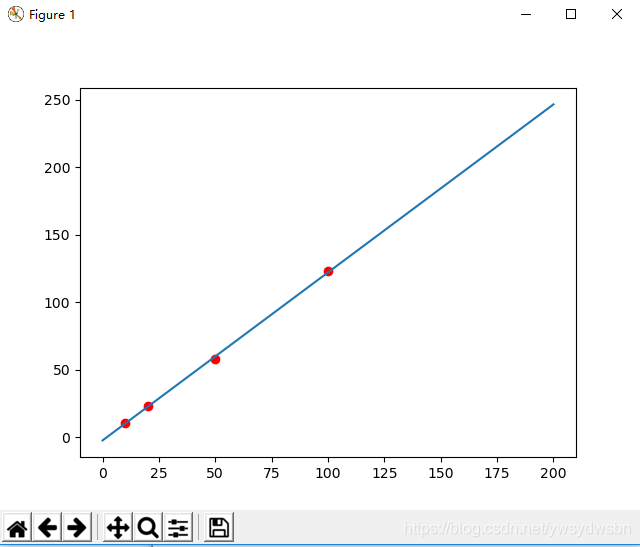
matlab实现例子

在matlab中，有现成的曲线拟合函数polyfit，其也是基于最小二乘原理实现的，具体用法为：

ans=polyfit(x,y,n). 其中x,y为待拟合点的坐标向量，n为多项式的阶数。

下面代码是用polyfit函数来做曲线拟合：

clearclcx=[2,4,5,6,6.8,7.5,9,12,13.3,15];[~,k]=size(x);y=[-10,-6.9,-4.2,-2,0,2.1,3,5.2,6.4,4.5];for n=1:9    ANSS=polyfit(x,y,n);  %用polyfit拟合曲线    for i=1:n+1           %answer矩阵存储每次求得的方程系数，按列存储       answer(i,n)=ANSS(i);   end    x0=0:0.01:17;    y0=ANSS(1)*x0.^n    ; %根据求得的系数初始化并构造多项式方程    for num=2:1:n+1             y0=y0+ANSS(num)*x0.^(n+1-num);    end    subplot(3,3,n)    plot(x,y,'*')    hold on    plot(x0,y0)endsuptitle('不同次数方程曲线拟合结果，从1到9阶')

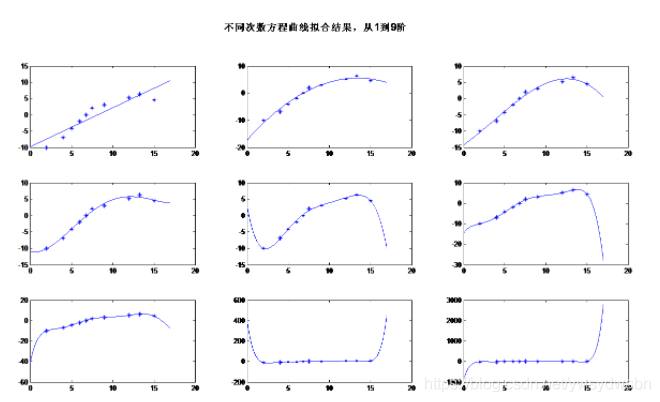
在分析时间与温度关系时，也会用到最小二乘法对其进行拟合。具体事例如下：

例如：对某日隔两小时测一次气温。设时间为ti,气温为Ci，i = 0，2 ，4，…，24。数据如下：

                表2 温度(Ci)随时间(ti)变化关系-----------------------------------------------------------ti      0  2   4  6   8  10  12  14  16  18  20  22  24-----------------------------------------------------------ci      15  14  14  16  20  23  28  27  26  25  22  18  16-----------------------------------------------------------

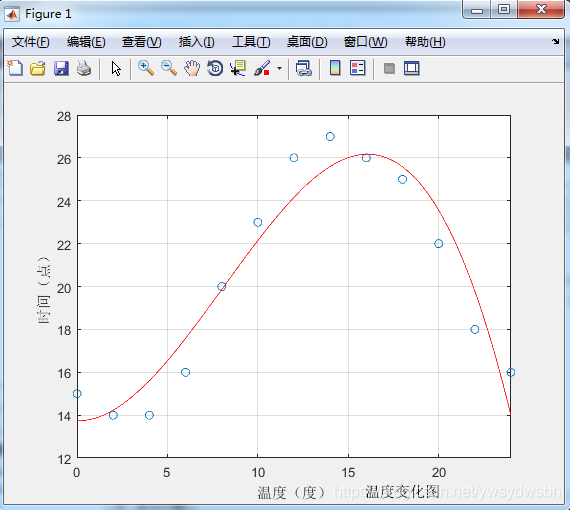
x = [0 2 4 6 8 10 12 14 16 18 20 22 24]y = [15 14 14 16 20 23 26 27 26 25 22 18 16]plot(x,y,'o')grid onhold on
% 三阶拟合  得到的 p = -0.0061    0.1474   -0.0246   13.7390是个多项式的系数% 即拟合的曲线y = -0.0061*x3 + 0.1474*x2 - 0.0246*x + 13.7390 （其中x3表示x的3次方，x2同理）p = polyfit(x,y,3)x1 = 0:0.01:24y1 = polyval(p,x1)plot(x1,y1,'r')axis([0 24 12 28])  % axis坐标轴范围设置xlabel('温度（度）');ylabel('时间（点）');title('温度变化图','position', [18,10])