CNN常用卷积方法一览
这篇文章的主题是卷积(Convlution)。想必熟悉CNN的你一定对卷积很熟悉了,或许也听过用过深度学习可分离卷积、转置卷积等概念和方法。那么目前为止,深度学习中都有哪些典型的卷积方式?本篇笔者就和大家一起来总结一下这些功能强大的卷积。本文的目录如下:
卷积的本质
常规卷积
单通道卷积
多通道卷积
3D卷积
转置卷积
1x1卷积
深度可分离卷积
空洞卷积
卷积的本质
在具体介绍各种卷积之前,我们有必要再来回顾一下卷积的真实含义,从数学和图像处理应用的意义上来看一下卷积到底是什么操作。目前大多数深度学习教程很少对卷积的含义进行细述,大部分只是对图像的卷积操作进行了阐述。以至于卷积的数学意义和物理意义很多人并不是很清楚,究竟为什么要这样设计,这么设计的原因如何。
追本溯源,我们先回到数学教科书中来看卷积。在泛函分析中,卷积也叫旋积或者褶积,是一种通过两个函数x(t)和h(t)生成的数学算子。其计算公式如下:
连续形式:
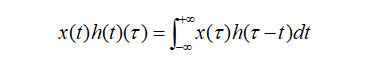
离散形式:
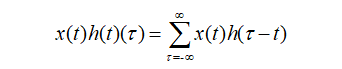
公式写的很清楚了,两个函数的卷积就是先将一个函数进行翻转(Reverse),然后再做一个平移(Shift),这便是"卷"的含义。而"积"就是将平移后的两个函数对应元素相乘求和。所以卷积本质上就是一个Reverse-Shift-Weighted Summation的操作。
数无形时少直观。我们用两个函数图像来直观的展示卷积过程和含义。两个函数x(t)和h(t)的图像如下图所示:
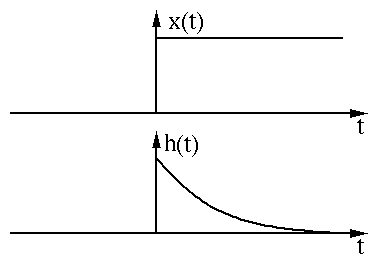
我们先对其中一个函数h(t)进行翻转(Reverse)操作:
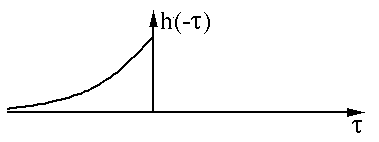
然后进行平移(Shift):
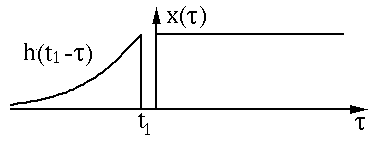
以上过程是为"卷"。然后是"积"的过程,因为是连续函数,这里相乘求和为积分形式,图中绿色部分即为相乘求和部分。
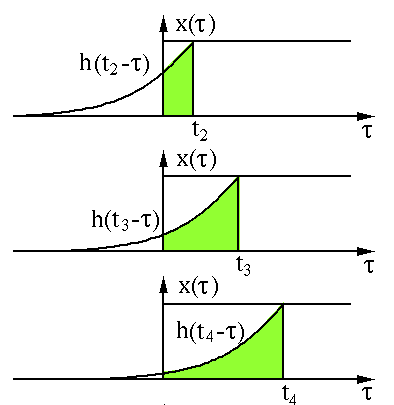
图像来自:
http://fourier.eng.hmc.edu/e161/lectures/convolution/index.html
那么为什么要卷积?直接元素相乘不好吗?就图像的卷积操作而言,笔者认为卷积能够更好提取区域特征,使用不同大小的卷积算子能够提取图像各个尺度的特征。卷积在信号处理、图像处理等领域有着广泛的应用。当然,之于深度学习而言,卷积神经网络主要用于图像领域。回顾了卷积的本质之后,我们再来一一梳理CNN中典型的卷积操作。
常规卷积
我们从最原始的图像卷积操作开始。因为图像有单通道图像(灰度图)和多通道图(RGB图),所以对应常规卷积方式可以分为单通道卷积和多通道卷积。二者本质上并无太大差异,无非对每个通道都要进行卷积而已。先来看单通道卷积。
在单通道卷积中,针对图像的像素矩阵,卷积操作就是用一个卷积核来逐行逐列的扫描像素矩阵,并与像素矩阵做元素相乘,以此得到新的像素矩阵。其中卷积核也叫过滤器或者滤波器,滤波器在输入像素矩阵上扫过的面积称之为感受野。假设输入图像维度为n*n*c,滤波器维度为f*f*n,卷积步长为s,padding大小为p,那么输出维度可以计算为:
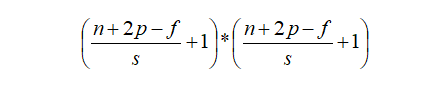
一个标准的单通道卷积如下图所示:
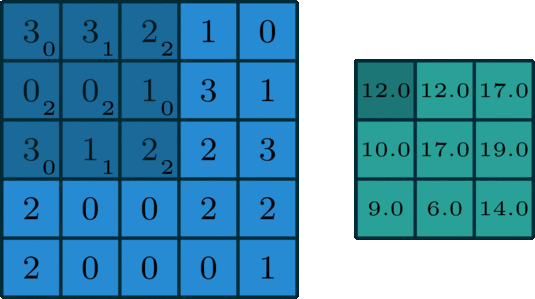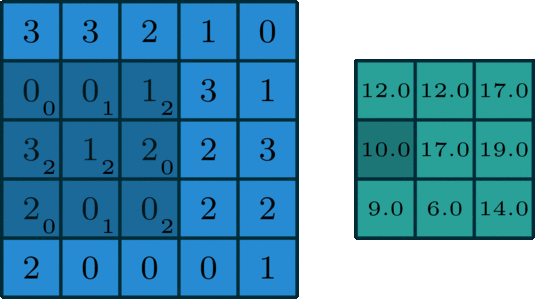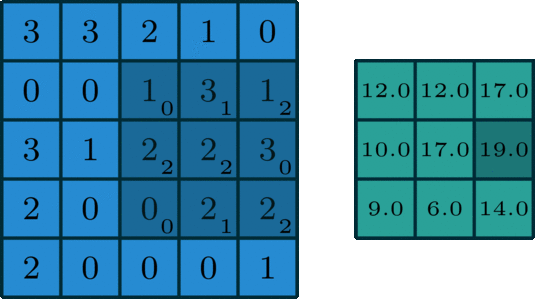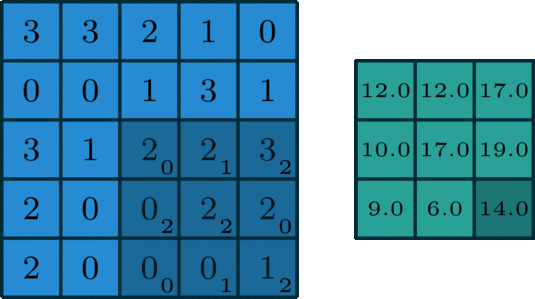
图像来自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
我们这里没有加入padding和stride等卷积要素,仅仅是为了说明一般的卷积过程。那么如何理解多通道(3通道)卷积呢?其实也很简单。比如说我们现在有一个5*5*3的RGB 3通道图像,我们可以将其看成是3张5*5图像的堆叠,这时候我们把原先的单通道滤波器*3,用3个滤波器分别对着三张图像进行卷积,将卷积得到三个特征图加总起来便是最后结果。这里强调一点:滤波器的通道数一定要跟输入图像的通道数一致,不然会漏下某些通道得不到卷积。现在我们用3*3*3的滤波器对5*5*3的输入进行卷积,得到的输出维度为3*3。这里少了通道数,所以一般我们会用多个3通道滤波器来进行卷积,假设我们这里用了10个3*3*3的滤波器,那最后的输出便为3*3*10,滤波器的个数变成了输出特征图的通道数。
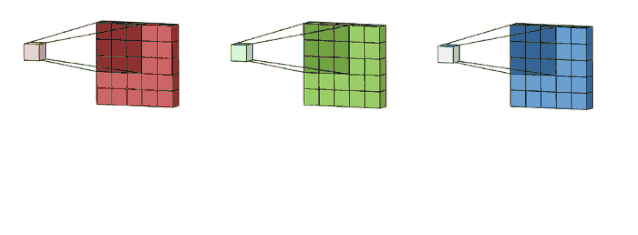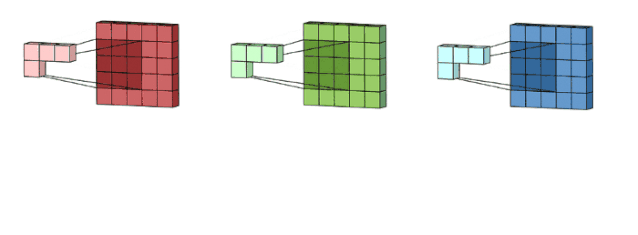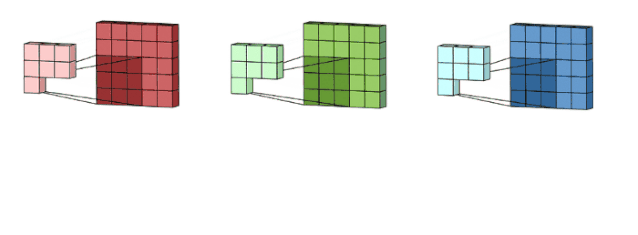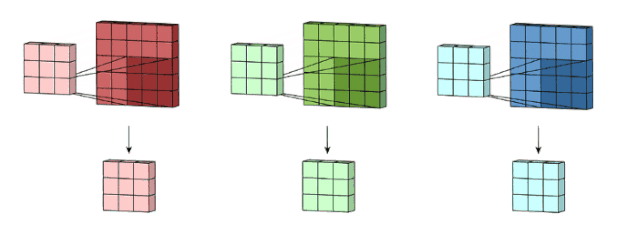

图像来自:
https://towardsdatascience.com/a-comprehensive-introduction-to-different-types-of-convolutions-in-deep-learning-669281e58215
我们也可以从3D的角度来理解多通道卷积:我们可以将3*3*3的滤波器想象为一个三维的立方体,为了计算立方体滤波器在输入图像上的卷积操作,我们首先将这个三维的滤波器放到左上角,让三维滤波器的27个数依次乘以红绿蓝三个通道中的像素数据,即滤波器的前9个数乘以红色通道中的数据,中间9个数乘以绿色通道中的数据,最后9个数乘以蓝色通道中的数据。将这些数据加总起来,就得到输出像素的第一个元素值。示意图如下所示:
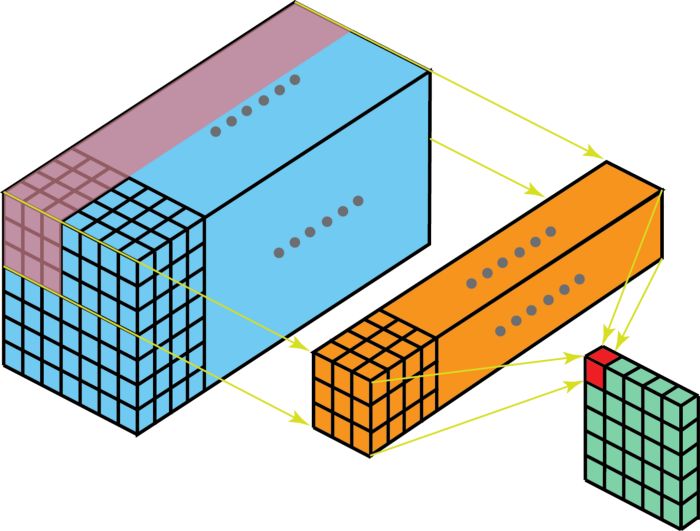
图像来自:
https://towardsdatascience.com/a-comprehensive-introduction-to-different-types-of-convolutions-in-deep-learning-669281e58215
3D卷积
将2D卷积增加一个深度维便可扩展为3D卷积。输入图像是3维的,滤波器也是3维的,对应的卷积输出同样是3维的。操作示意图如下:
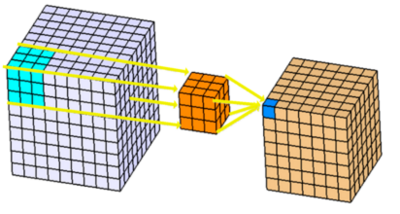
可以想象一下3D卷积的动态图。用一个2*2*2的3D滤波器对一个4*4*4的输入图像进行3D卷积,可以得到一个3*3*3的输出。
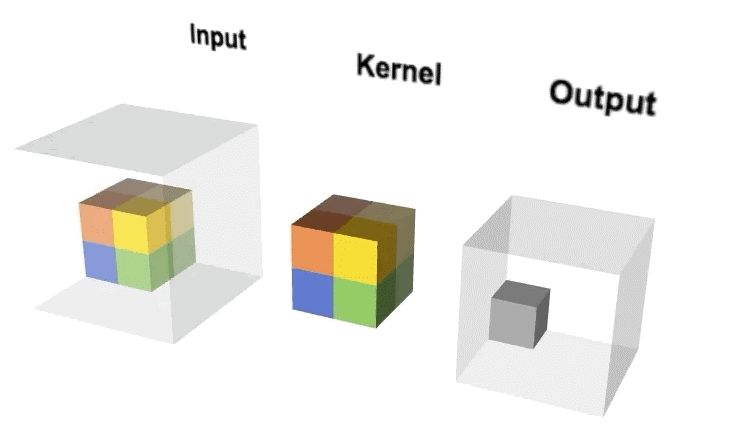
我们可以把2D卷积的计算输出公式进行扩展,可以得到3D卷积的输出维度计算公式。假设输入图像大小为a1*a2*a3,通道数为c,过滤器大小为f*f*f*c,滤波器数量为n,则输出维度可以表示为:
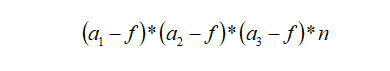
3D卷积在医学影像数据、视频分类等领域都有着较为广泛的应用。相较于2D卷积,3D卷积的一个特点就是卷积计算量巨大,对计算资源要求相对较高。
转置卷积
转置卷积(Transposed Convolution)也叫解卷积(Deconvolution),有些人也将其称为反卷积,但这个叫法并不太准确。大家都知道,在常规卷积时,我们每次得到的卷积特征图尺寸是越来越小的。但在图像分割等领域,我们是需要逐步恢复输入时的尺寸的。如果把常规卷积时的特征图不断变小叫做下采样,那么通过转置卷积来恢复分辨率的操作可以称作上采样。
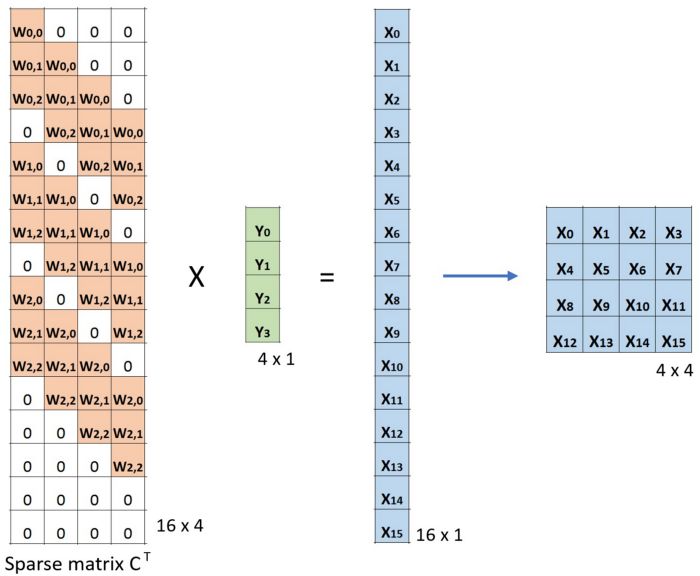
本质上来说,转置卷积跟常规卷积并无区别。不同之处在于先按照一定的比例进行padding来扩大输入尺寸,然后把常规卷积中的卷积核进行转置,再按常规卷积方法进行卷积就是转置卷积。假设输入图像矩阵为X,卷积核矩阵为C,常规卷积的输出为Y,则有:
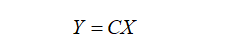
两边同时乘以卷积核的转置CT,这个公式便是转置卷积的输入输出计算。
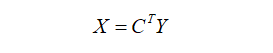
假设输入大小为4*4,滤波器大小为3*3,常规卷积下输出为2*2,为了演示转置卷积,我们将滤波器矩阵进行稀疏化处理为4*16,将输入矩阵进行拉平为16*1,相应输出结果也会拉平为4*1,图示如下:
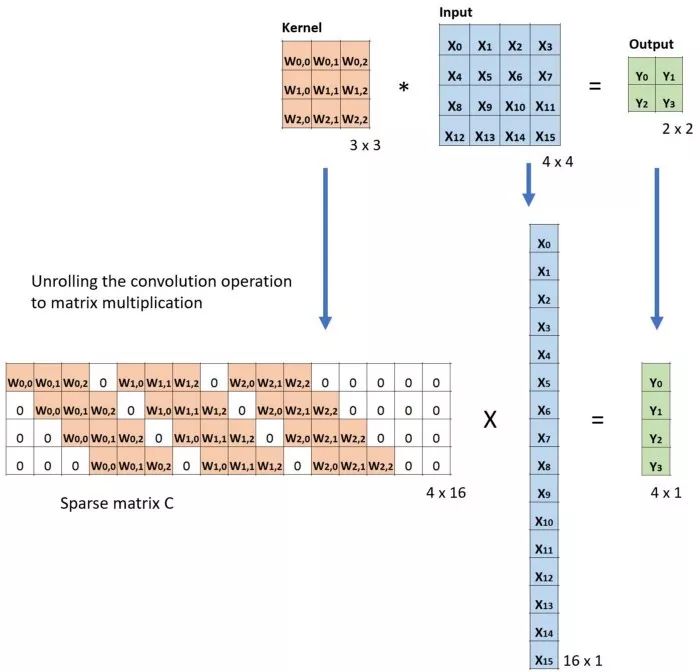
然后按照转置卷积的做法我们把卷积核矩阵进行转置,按照X=CTY进行验证:
图像来自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
关于转置卷积的最后一个问题是输入输出尺寸计算。我们将常规卷积的计算公式转化一下即可得到转置卷积的换算公式:
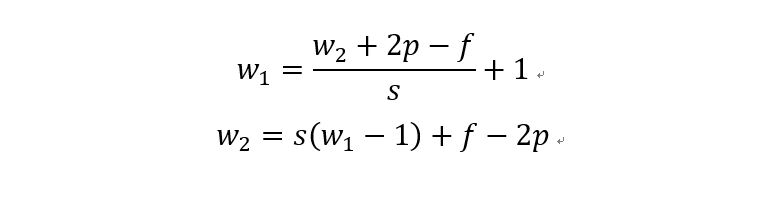
第一个公式就是上面提到的常规卷积的输入输出换算公式,第二个公式为转置卷积的输入输出换算公式。其中,s常规卷积步长,p是常规卷积的padding,f为滤波器大小。虽说公式推导起来简单,但考虑到(w2+2p-f)/s极有可能出现不能整除的情况,所以常规卷积和转置卷积之间的转换关系就需要分为两种情况。
第一种就是可以直接整除的。即当(w2+2p-f)%s=0时,常规卷积与转置卷积之间的换算关系。我们以一组无padding条件下常规卷积和转置卷积的对比动图:
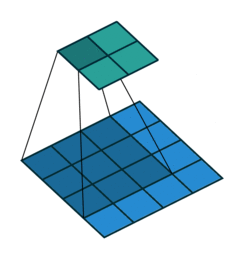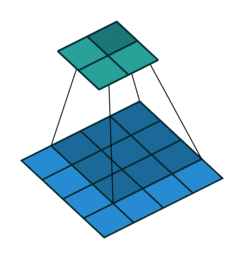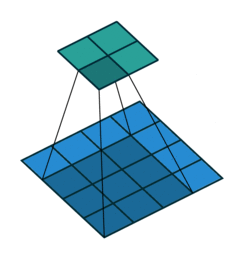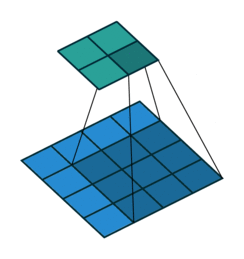
常规卷积
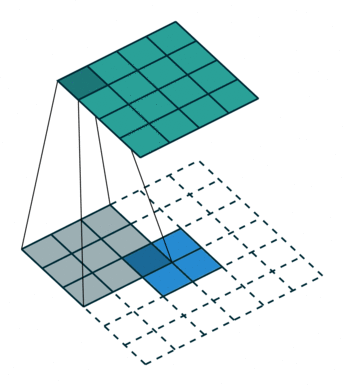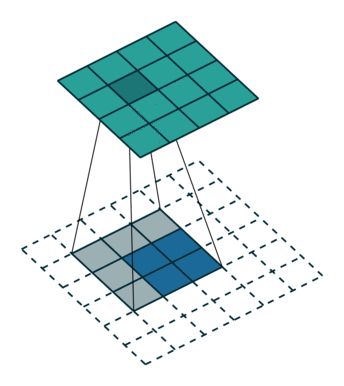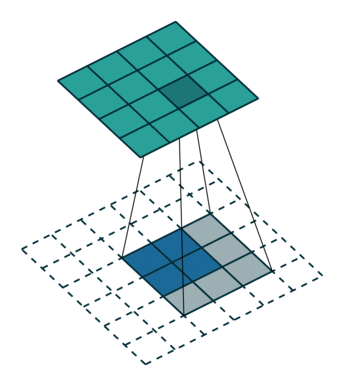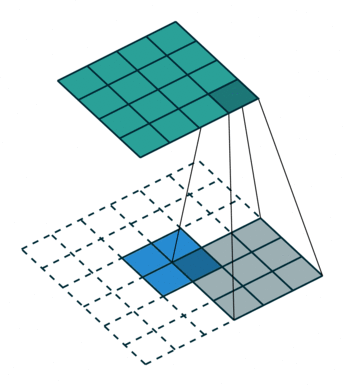
转置卷积
图像来自:
https://github.com/vdumoulin/conv_arithmetic
在上图常规卷积中,输入为2*2,滤波器为3*3,根据上述第一个公式可得输出为(4+2*0-3)/1 + 1=2,这时候是可以整除的,所以输出为2*2。对应到转置卷积中:1*(2-1)+3-2*0=4,即转置卷积的输出为4*4。
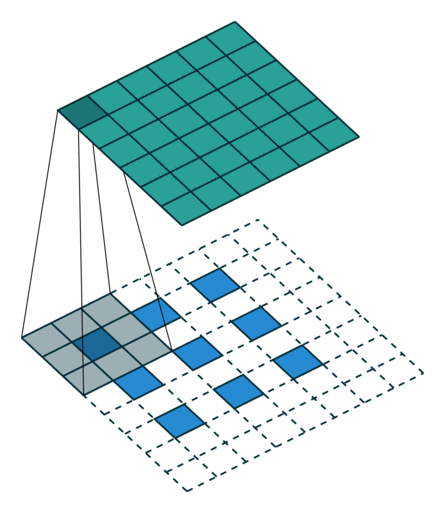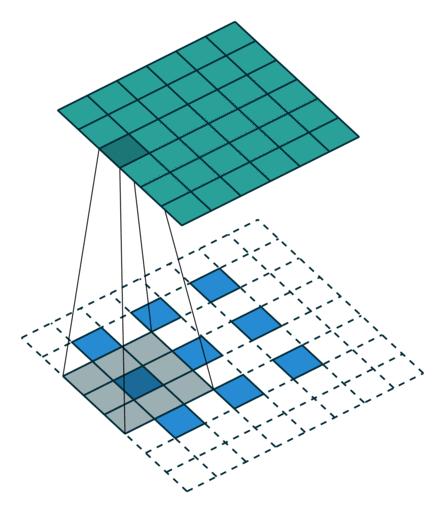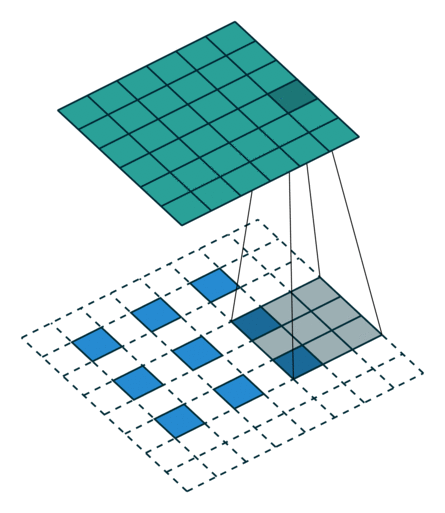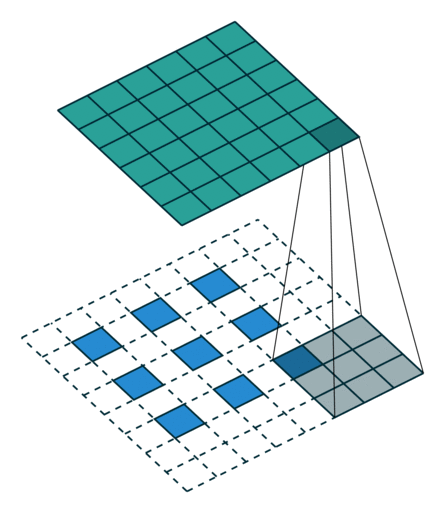
第二种就是略微复杂一点的不能整除的情况。常规卷积时不能整除的情况也叫odd卷积。即当(w2+2p-f)%s!=0时,常规卷积与转置卷积之间的换算关系如何。在进行odd卷积时,遇到不能整除的情况下我们通过会进行取整操作,因而在常规卷积时有时候会忽略一小部分像素没有进行卷积,这在转置卷积时需要加回来。我们同样以一组odd卷积例子来进行说明。
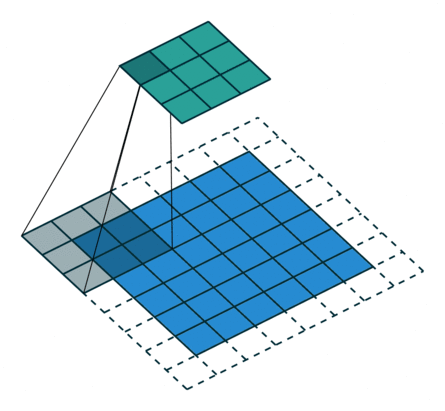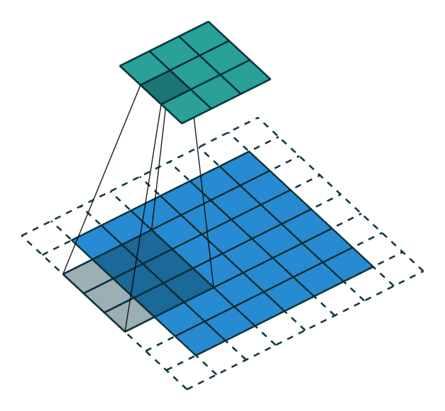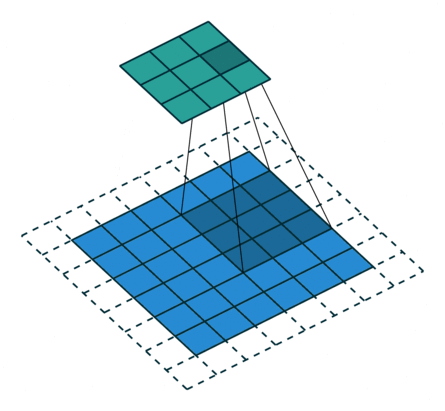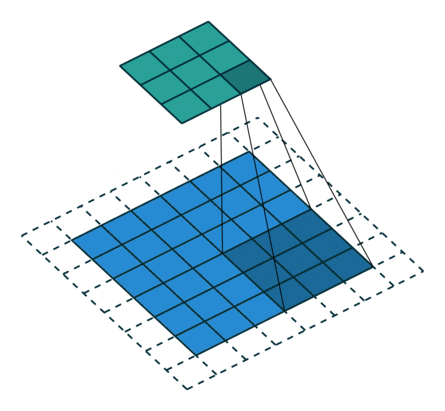
odd常规卷积
odd转置卷积
图像来自:
https://github.com/vdumoulin/conv_arithmetic
如上图所示。在odd常规卷积中,我们用一个3*3的滤波器对6*6的输入进行卷积,padding=1,stride=2,根据公式(6+2*1-3)/2,发现不能整除,这里我们取整为3,那么输出特征图大小为3*3。因为做了取整操作,大家可以看到图中最右边一列和最下边一行的padding是没有加入到卷积计算中的。这部分因取整而舍去的数据需要我们在转置卷积时给加回来。所以,对应的转置卷积的输入输出换算公式可以更改为:
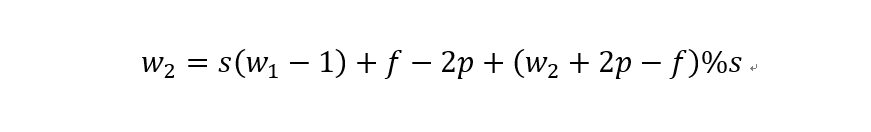
在上图中,我们输入尺寸为3*3,卷积滤波器大小也为3*3,padding为1,但这里stride等于2,有同学可能会问,图中卷积核明明只移动一个步长啊为啥stride=2?图中确实只移动了一个步长,但大家可以注意到我们输入里插入了很多白色块,也就是0,从当前元素值移动到下一个元素值,实际上是经过两个步长的。所以,这里的输出尺寸为2*(3-1)+3-2*1+1=6。这便是转置卷积。
1x1卷积
1x1卷积的伟大发明来自于2014年GoogLeNet的inception v1,其主要作用在于可以降维节省计算成本。1x1卷积在卷积方式上与常规卷积并无差异,主要在于其应用场景和功能。
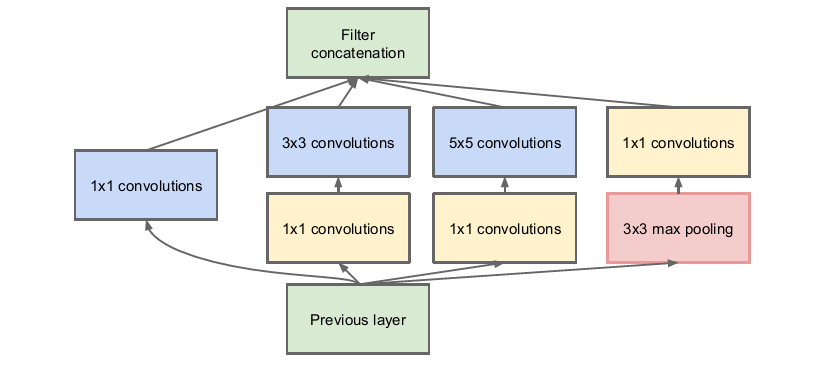
inception v1模块
下面我们来看1x1卷积到底有什么功效。假设现在我们有28*28*192的输入,使用32个5*5*192的卷积核对其进行卷积,那么输出为28*28*32,好像没什么特别之处。我们来看一下它的计算量,对于输出中的每一个元素值都要执行5*5*192次计算,所以这次卷积的计算量为:28*28*32*5*5*192=120422400。5*5卷积的运算量直接上亿了。
那现在看看1x1卷积会如何。我们先用16个1*1*192的卷积核对输入进行卷积,输出尺寸为28*28*16,再用32个5*5*16的卷积核对其进行卷积,输出为28*28*32。经历两次卷积同样得到28*28*32的输出,来看一下其中的计算量。第一次卷积:28*28*16*192=2408448,第二次卷积28*28*32*5*5*16=10035200,两次卷积合计计算量约为120万,将较于直接的5*5卷积,1x1卷积的计算量直接减少了10倍,能够在保证网络性能的情况下极大幅度的节约计算成本。这便是1x1卷积。
深度可分离卷积
从维度的角度看,卷积核可以看成是一个空间维(宽和高)和通道维的组合,而卷积操作则可以视为空间相关性和通道相关性的联合映射。从inception的1x1卷积来看,卷积中的空间相关性和通道相关性是可以解耦的,将它们分开进行映射,可能会达到更好的效果。
深度可分离卷积是在1x1卷积基础上的一种创新。主要包括两个部分:深度卷积和1x1卷积。深度卷积的目的在于对输入的每一个通道都单独使用一个卷积核对其进行卷积,也就是通道分离后再组合。1x1卷积的目的则在于加强深度。下面以一个例子来看一下深度可分离卷积。
假设我们用128个3*3*3的滤波器对一个7*7*3的输入进行卷积,可得到5*5*128的输出。如下图所示:
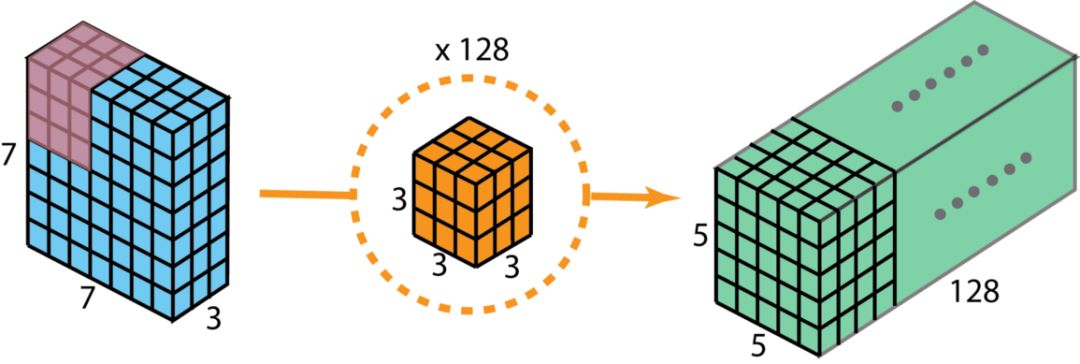
图像来自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
其计算量为5*5*128*3*3*3=86400。
现在看如何使用深度可分离卷积来实现同样的结果。深度可分离卷积的第一步是深度卷积。这里的深度卷积,就是分别用3个3*3*1的滤波器对输入的3个通道分别做卷积,也就是说要做3次卷积,每次卷积都有一个5*5*1的输出,组合在一起便是5*5*3的输出。
现在为了拓展深度达到128,我们需要执行深度可分离卷积的第二步:1x1卷积。现在我们用128个1*1*3的滤波器对5*5*3进行卷积,就可以得到5*5*128的输出。完整过程如下图所示:
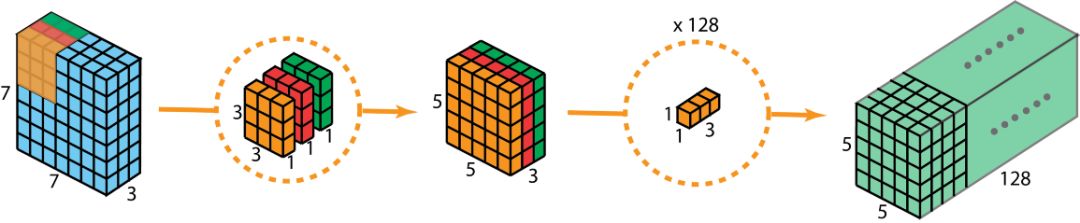
图像来自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
那么我们来看一下深度可分离卷积的计算量如何。第一步深度卷积的计算量:5*5*1*3*3*1*3=675。第二步1x1卷积的计算量:5*5*128*1*1*3=9600,合计计算量为10275次。可见,相同的卷积计算输出,深度可分离卷积要比常规卷积节省12倍的计算成本。
典型的应用深度可分离卷积的网络模型包括xception和mobilenet等。本质上而言,xception就是应用了深度可分离卷积的inception网络。
空洞卷积
空洞卷积也叫扩张卷积或者膨胀卷积,简单来说就是在卷积核元素之间加入一些空格(零)来扩大卷积核的过程。我们用一个扩展率a来表示卷积核扩张的程度。比如说a=1,2,4的时候卷积核核感受野如下图所示:

图像来自:
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
加入空洞之后的实际卷积核尺寸与原始卷积核尺寸之间的关系:
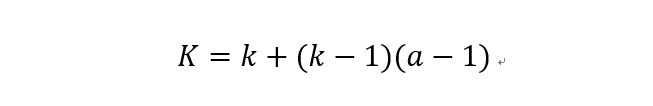
其中k为原始卷积核大小,a为卷积扩展率,K为经过扩展后实际卷积核大小。除此之外,空洞卷积的卷积方式跟常规卷积一样。a=2时的空洞卷积的动态示意图如下所示:
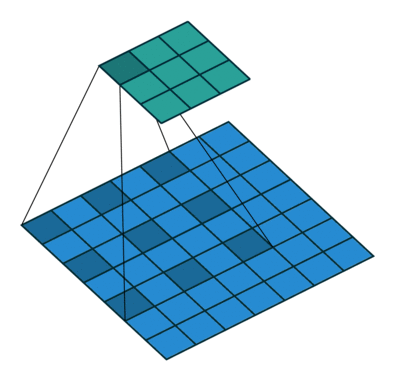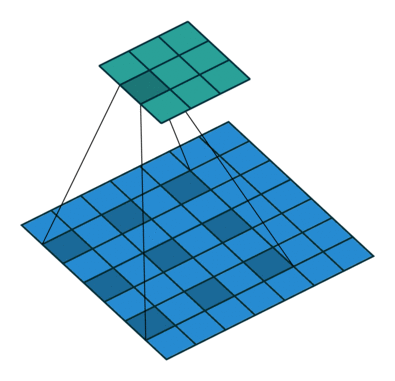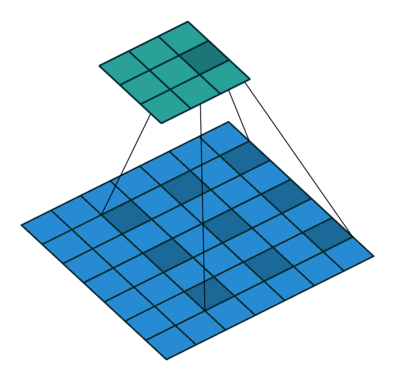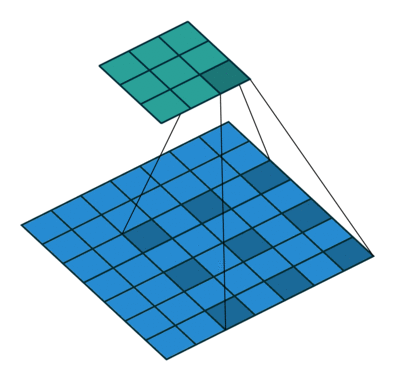
图像来自:
https://github.com/vdumoulin/conv_arithmetic
那么空洞卷积有什么好处呢?一个直接作用就是可以扩大卷积感受野,空洞卷积几乎可以在零成本的情况下就可以获取更大的感受野来扩充更多信息,这有助于在检测和分割任务中提高准确率。空洞卷积的另一个优点则是可以捕捉多尺度的上下文信息,当我们使用不同的扩展率来进行卷积核叠加时,获取的感受野就丰富多样。
参考资料:
往期精彩:
求个在看
