【深度学习】深入理解LSTM
Author:louwill
From:深度学习笔记
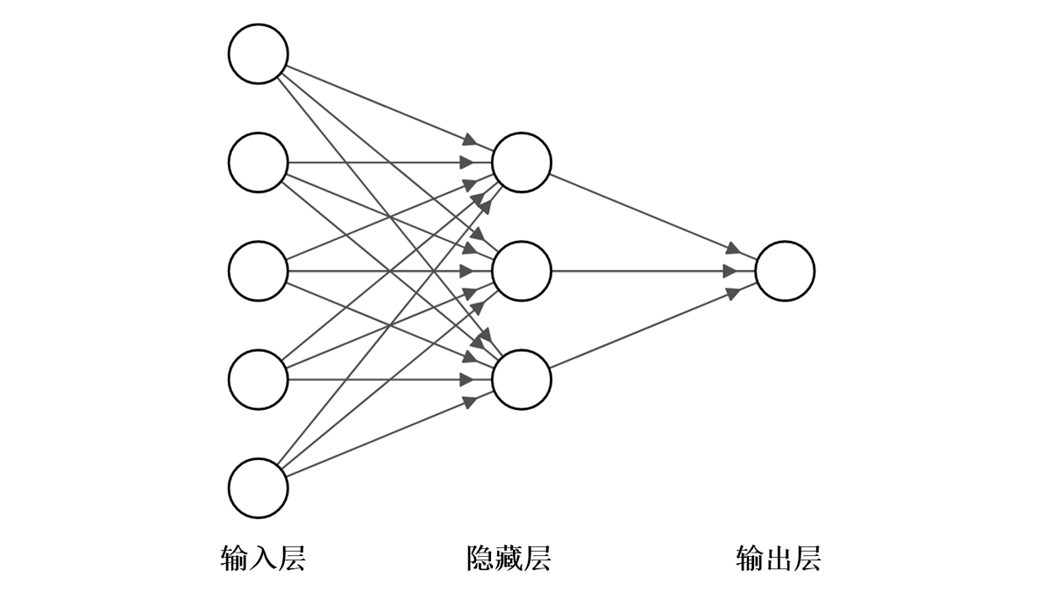
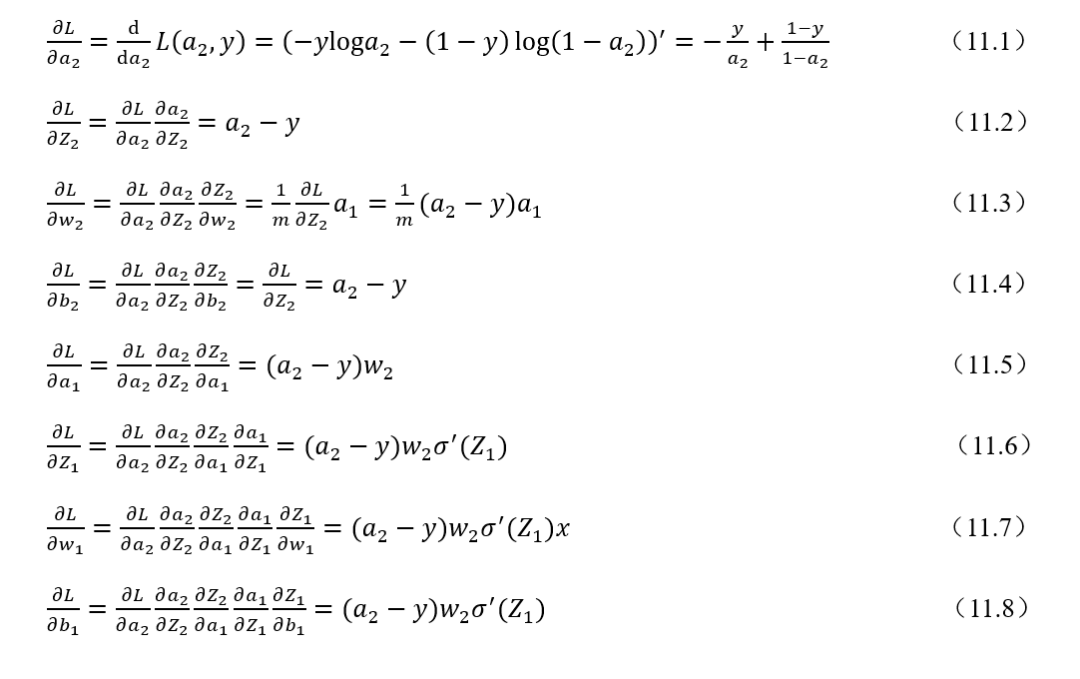
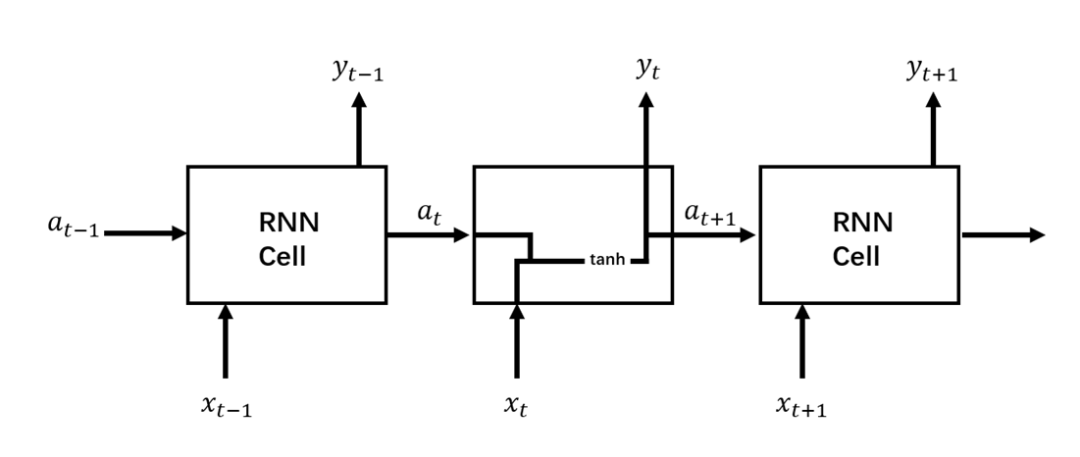
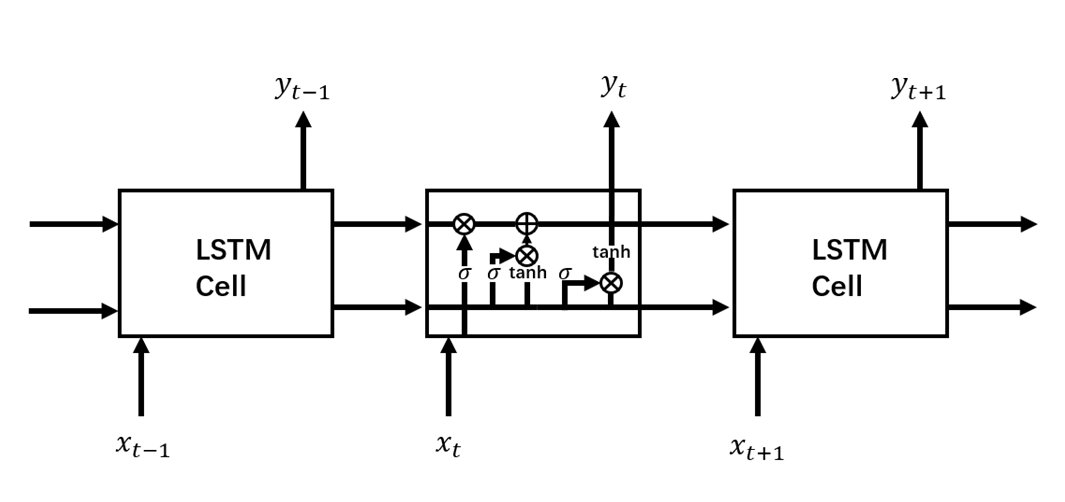
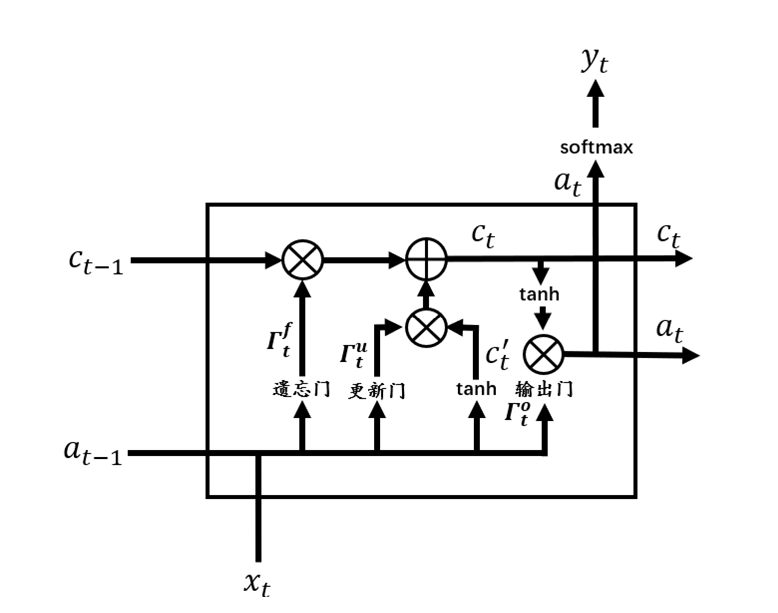
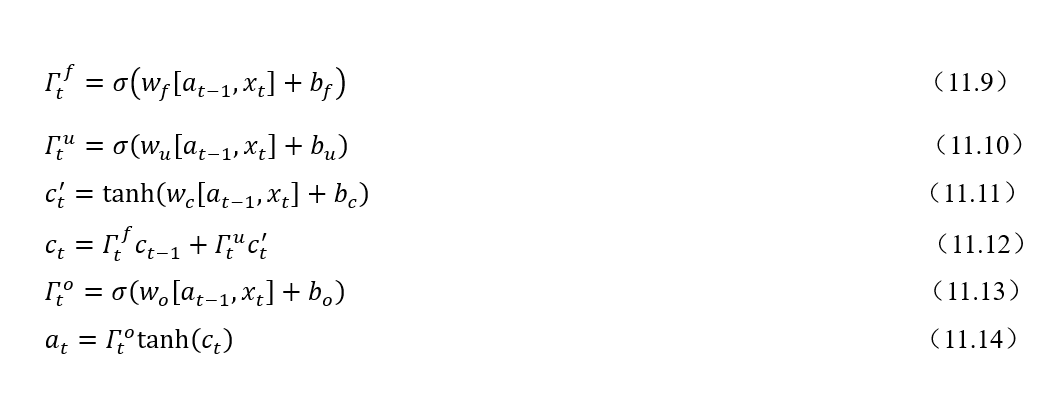
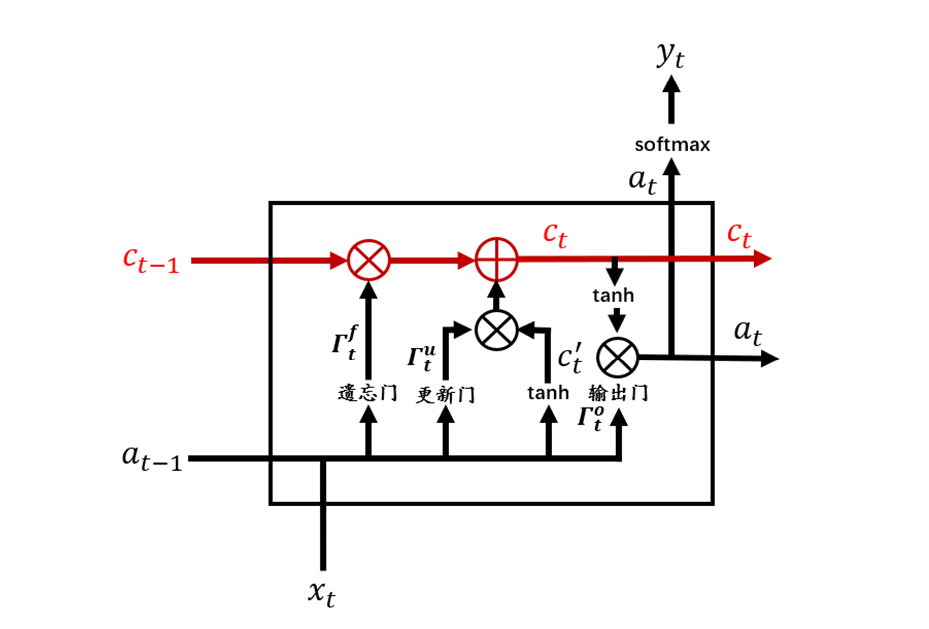
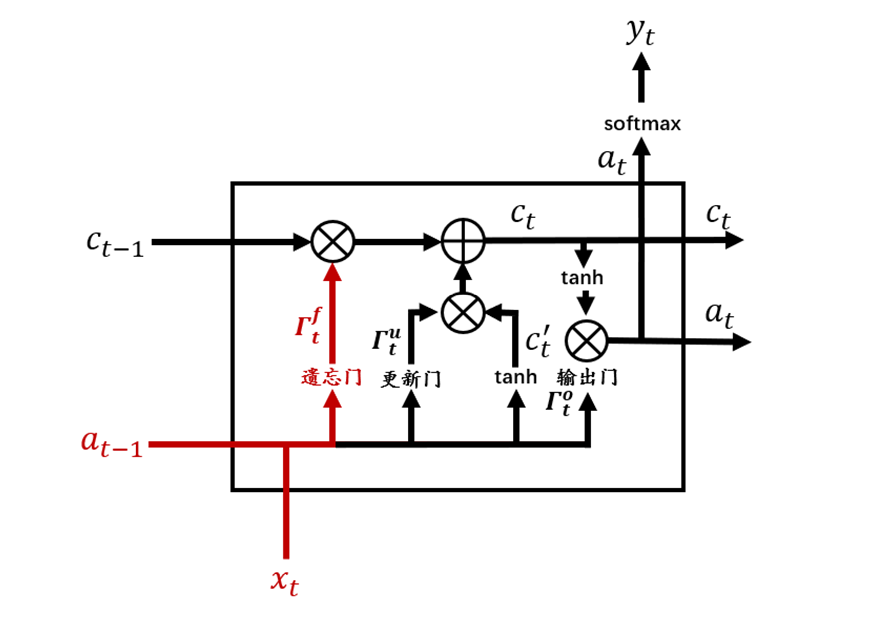
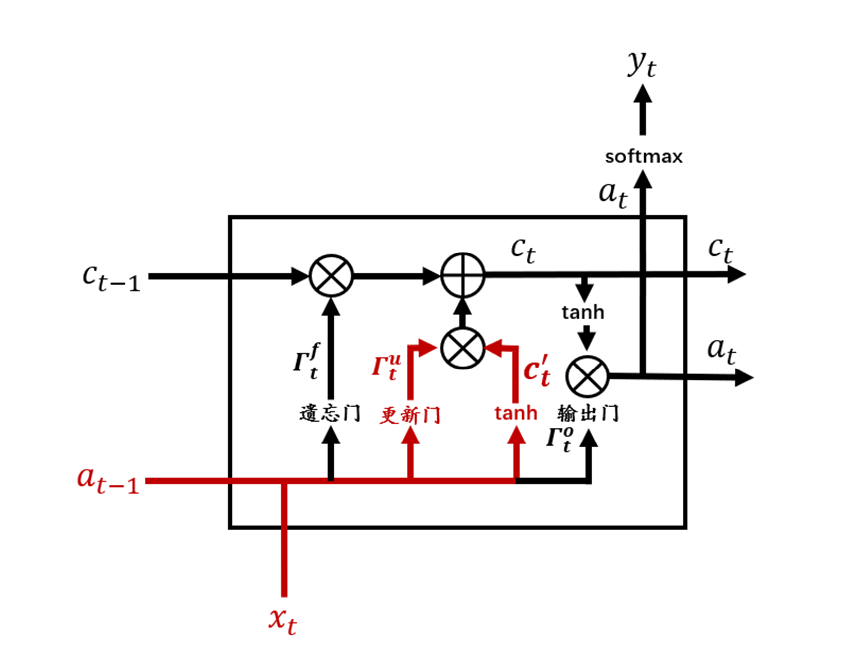
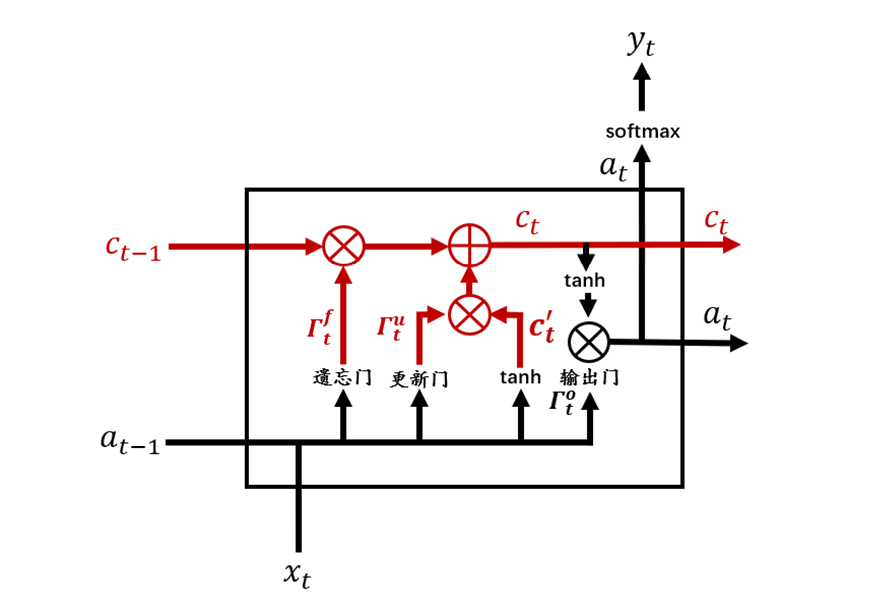
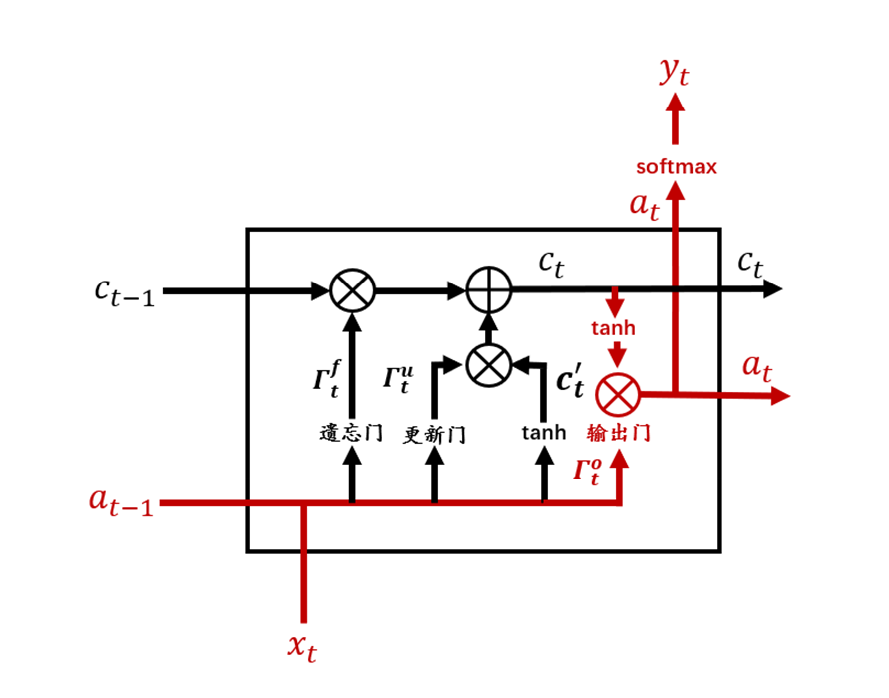
往期精彩回顾
获取一折本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/662nyZF
本站qq群704220115。
加入微信群请扫码进群(如果是博士或者准备读博士请说明):
评论
 下载APP
下载APPAuthor:louwill
From:深度学习笔记

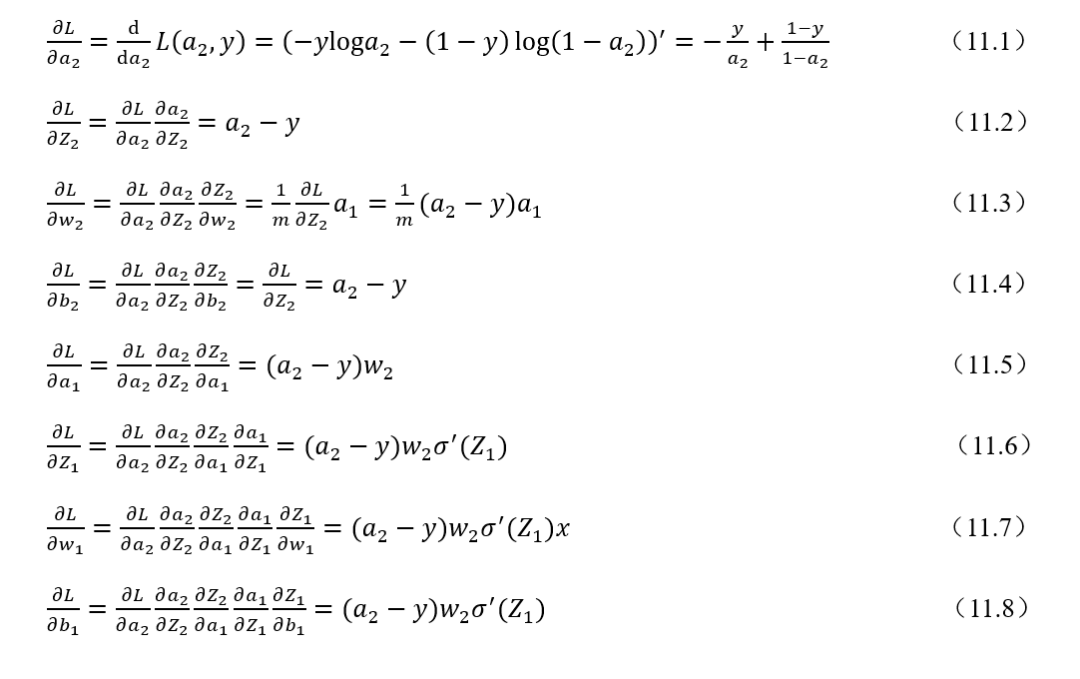



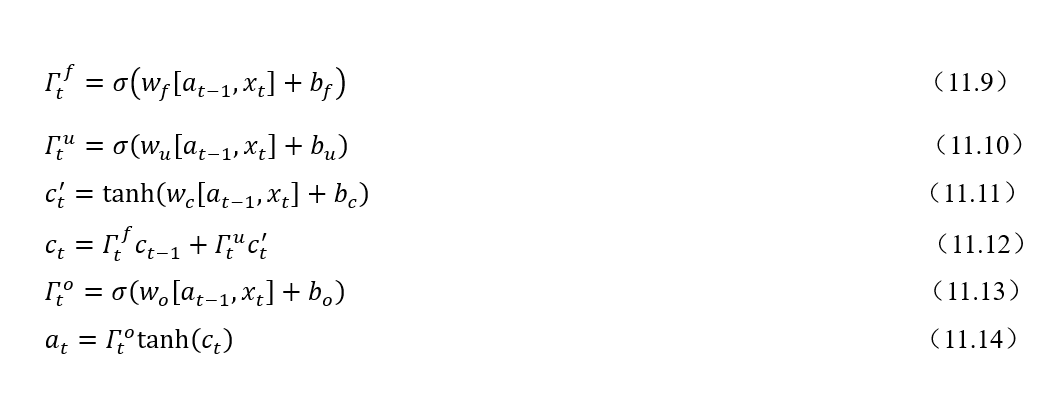





往期精彩回顾
获取一折本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/662nyZF
本站qq群704220115。
加入微信群请扫码进群(如果是博士或者准备读博士请说明):