【算法】五分钟快速了解代码复杂度

大 O 复杂度表示法

如何在不运行代码的情况下，通过”肉眼“计算出一段代码的执行时间

一段简单的 Python 代码，求1,2,3…n的累加和

1def cal(n):
2  sum = 0
3  for i in range(n):
4    sum += i
5  return sum

对于上面的一段简单代码，我们输入不同的 n 值，来看一下代码执行的效果

n = 5

n = 10

其实上面的代码实在是简单，不用说也知道 n 不同时，代码的执行过程是怎样的

而我们这里要关注的重点是代码的3、4行，当 n = 5 时，3、4行代码执行了5遍，当 n = 10 时，又执行了10遍，其实我们依次类推可以知道，3、4行代码永远都是执行 n 遍，那么此时对于上面代码的时间复杂度 T(n)，我们就可以表示为

T(n) = O(n)

这就是我们常常说的大 O 表示法

当然了，通过上面的描述，还是有一些抽象的，下面我们再通过一个小栗子来看一下

查找文件

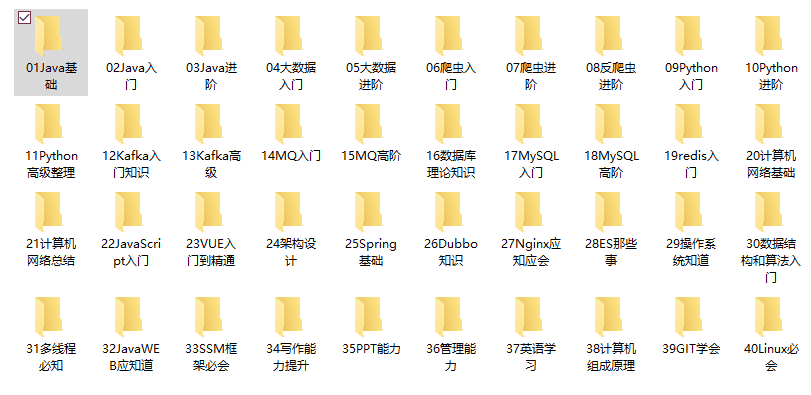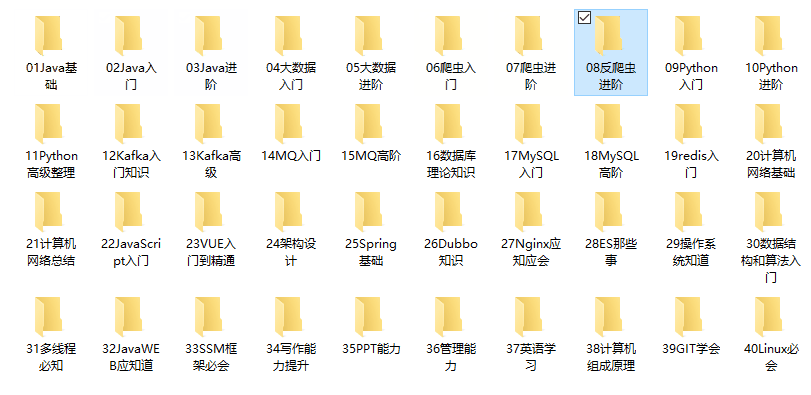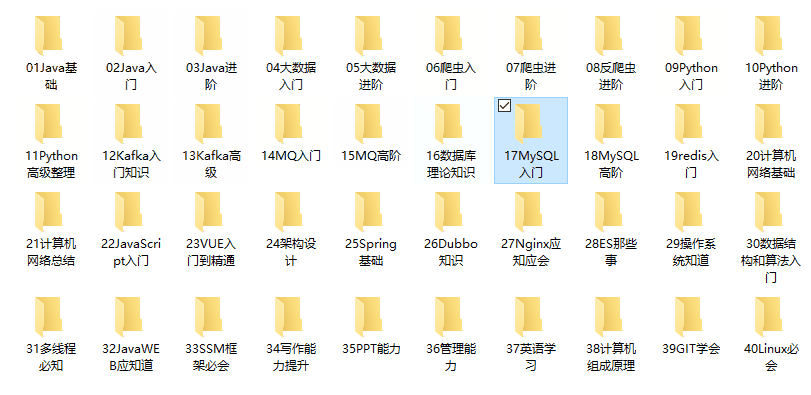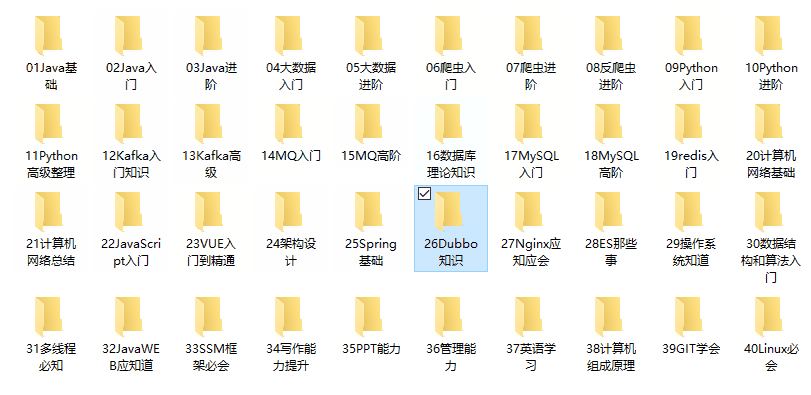
比如我这里整理的编程类资源

经过多年的努力，终于学（收）会（集）了图中的所有知识，那么如果某一天，我想写一段代码来查找 Dubbo 教程，应该如何实现呢

方法1

依次一个一个的查找

实现代码为

1def find_source(source_list, name):
2    for i in source_list:
3        if i == name:
4            return i

这样我们需要一直循环到文件夹26才可以找到 Dubbo 资源，当资源少的时候还可以如果是海量资源，那么效率太低了

方法2

从中间开始找，如果发现小了，就把左边的都去掉，再在剩下的文件中往中间开始找，以此类推

这样的二分查找，我们只需要在第五次查找的时候就拿到想要的资源

 1def find_source(source_list, name):
 2    min = 0
 3    ma = len(source_list)-1
 4    while min <= max:
 5        mid = (min+max)/2
 6        if source_list[mid] == name:
 7            return "get source at %s" % mid
 8        if source_list[mid] < name:
 9            min = mid + 1
10        else:
11            max = mid - 1
12    return "no source here!"

可以清晰的看出，第二种方法快了很多，而且在资源数量越大的时候，越能体现

对于方法1，通过大 O 表示法可以表示为

T(n) = O(n)

对于方法2，通过大 O 表示法可以表示为

T(n) = O(logn)

很明显，随着 n 的增加，logn 会远远小于 n，也即是方法2的速度会远远快于方法1，这一点我们在上面的实践当中也有了证明

当然对于常见的复杂度，还有如下这些

O(1), O(n), O(logn), O(nlogn), O(n^2)

一般来说，他们的排序顺序是这样的

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2)

最坏时间复杂度

我们再回到最开始的简单代码

1def cal(n):
2  sum = 0
3  for i in range(n):
4    sum += i
5  return sum

可以简单的把上述代码分为两块，代码行2和代码行3、4
对于行2，复杂度为 O(1)，对于行3、4，复杂度为 O(n)，一般情况下，我们分析一段代码的复杂度时，基本采用的是复杂度比较高的那一部分，也即是上述代码的复杂度为 O(n)

这里其实还涉及到了两个概念，就是最好情况时间复杂度和最坏情况时间复杂度，同样可以看出，O(1) 就是最好情况时间复杂度，而 O(n) 就是最坏的情况

好了，以上就是今天我们要分享的内容，喜欢就给个”在看“吧