Github 上有与文章配套的 jupyter notebook，和文章配合食用，效果更佳。

https://github.com/BSlience/transformer-all-in-one

本文主要回答以下几个问题：

• Attention 机制是用来做什么的 ？

• Self-attention 是怎么从 Attention 过度过来的 ？

• Attention 和 self-attention 的区别是什么 ？

• Self-attention 为什么能 work ？

• 怎么用 Pytorch 实现 self-attention ？

• Transformer 的作者对 self-attention 做了哪些 tricks ？

• 怎么用 Pytorch/Tensorflow2.0 实现在 Transfomer 中的 self-attention ？

• 完整的 Transformer Block 是什么样的？

• 怎么捕获序列中的顺序信息呢 ？

• 怎么用 Pytorch 实现一个完整的 Transformer 模型？

Attention 机制是用来做什么的 ？

Attention机制最早的提出是针对与序列模型的，出处是Bengio大神在2015年的这篇文章：

Neural Machine Translation by jointly learning to align and translate, Bengio et. al. ICLR 2015

https://arxiv.org/pdf/1409.0473.pdf

在这篇文章中其实并没有经常性的提到attention（其实只有3次），这个词流行起来其实是在后来的一些工作中，被很多work提及到。在这篇文章中，我试图在更common的视角下去理解attention的机制，而不是使用论文中在translation任务中的应用。

我们要说attention机制其实是借鉴了生物在观察和学习行为中的过程，也就是说我们人来通常在观察和学习的时候，都是通过快速的获取全局的信息，建立起对于事物的需要重点观察或者学习的区域，这些需要重点关注的目标区域，就是我们注意力的焦点。然而，就和我们日常生活中处理事情一样，我们没有办法同时处理所有的事情，我们会给他们分出优先级。同样的，注意力也会有一个权重值，从而更专注的聚焦在某些关键的信息上。

我们把attention放到不同case里，再去看看这种注意力不同的解释。

首先我们看看在视觉领域，我们应该怎么去理解attention：

当我们去看上面这张照片的时候，我们首先就是先去看整体，这里有车、有街道、还有很多的广告牌，不知道大家是否有感受到，当我开始描述这些的时候，其实就是我把注意力放在了这些上面了。那当我们想要跟深入了解这张图片的时候，我就要把注意力放的更聚焦。比如说，我想知道这是拍的哪里，那我可能会试着去看看广告牌上的文字，看这些文字是不是能给我一些启示。

就像上面这张图一样，我们可能会试着把注意力放到不同的区域，那我们就能够得到更多的关于不同角度的信息。这些信息，正是我们希望在图像处理的时候希望得到的。

我们再来看看再自然语言处理中，attention机制表示的又是什么呢？

比如说上面的这句话，“她正在吃一个绿色的苹果”，这里我们可以比较清楚的看到，“吃”和“苹果”有很强的联系，那我们就希望在处理吃这个单词的时候，能够在语义中，包含一定的苹果的信息，这样能够帮助我们更好的理解“吃”这个动作。“绿色的”和“苹果”也是一样的，attention的机制能够帮助我们在处理单个的token的时候，带有一定的上下文信息。这就像是一种“软性记忆”一样，帮助我们记住上下文中包含的信息。

当我们看一篇文章的时候，其实也是类似的。我们从拿到一篇文章开始，首先关注的也只是一些关键性的词语，这些关键性的词语，就能够帮助我们快速的判断文章的内容和结构。这些场景就是我们在一些具体场景中对attention的应用。

那接下来，我们再来看看，attention具体是怎么工作的？

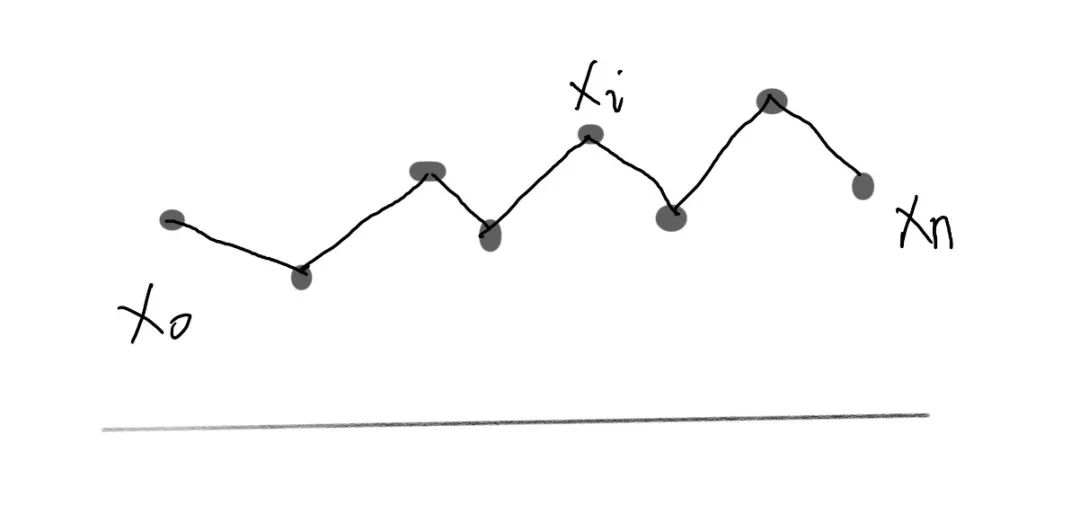
假设我们的时间序列：  ，我们把它放到坐标轴上，就是上面这张图的样子。

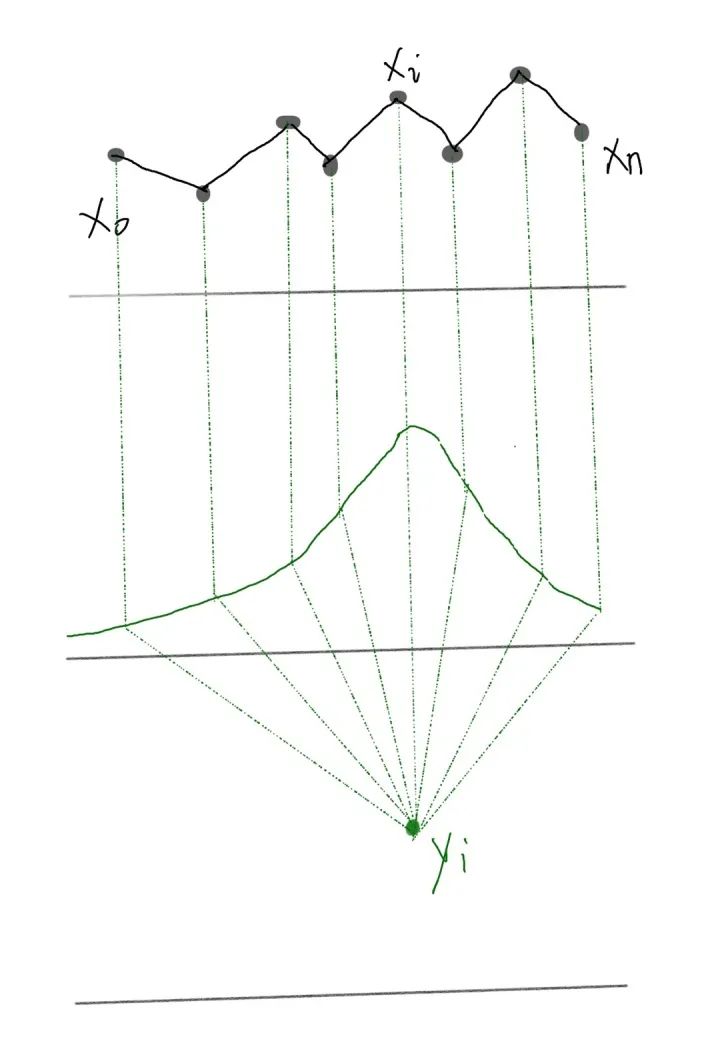
这些点是我们从整体数据中采样出来的，这里有很多的噪音（noisy），我们想办法能不能通过一些方法，得到这些数据的更好的表示，从而能够使噪音减少。那这里面我们可以使用re-weighting的操作，让我们的这些点都包含一些其他点的信息，使得所有的数据能够更平滑一些。我们定义这些re-weighting的参数为  ，我们使用这些weights就能够得到一个点的新的表示  。

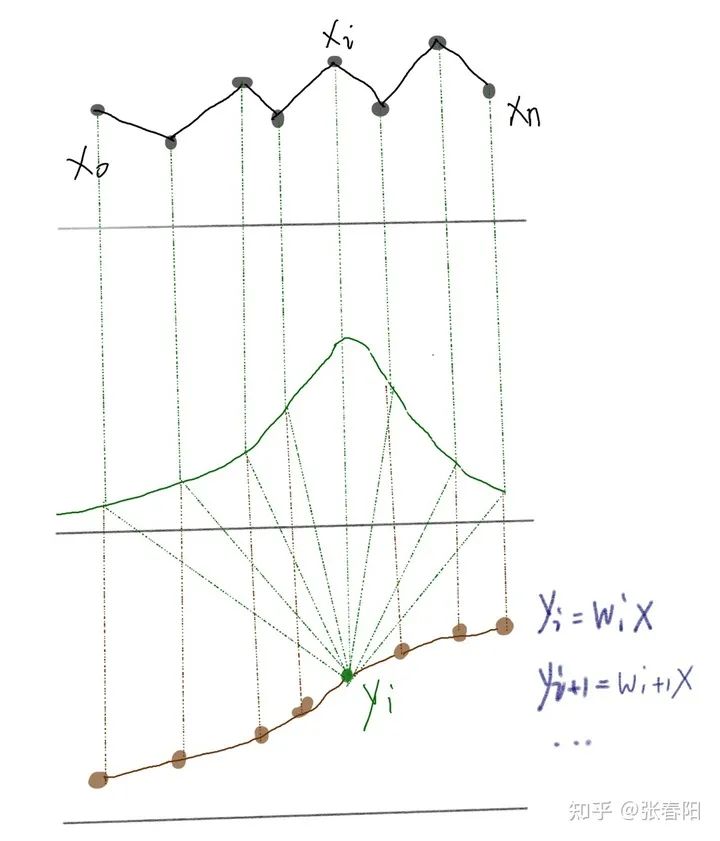
Self-attention是一个序列到序列的操作：一个向量的序列作为输入，一个向量的序列作为输出。我们把输入的序列定义为  ，并且与它相关的输出向量是  。这两个向量的维度都是  。那么对于每一个点  ，我们都可以通过一个不同的权重值，来将它转化为一个新的序列，这个新的序列就可能是我们原始序列的一个更好的表示，这些  就是一组attention的值。

来看一个动图的例子：

以上就是attention机制。

Self-attention 是怎么从 Attention 过度过来的 ？

Self-attention就本质上是一种特殊的attention。它和attention的区别我会在下一个章节介绍，这里先来介绍下self-attention，这种应用在transformer中最重要的结构之一。

上面我们介绍了attention机制，它能够帮我们找到子序列和全局的attention的关系，也就是找到权重值  。self-attention对于attention的变化，其实就是寻找权重值的过程不同。下面，我们来看看self-attention的运算过程。

为了能够产生输出的向量  ，self-attention其实是对所有的输入做了一个加权平均的操作，这个公式和上面的attention是一致的。

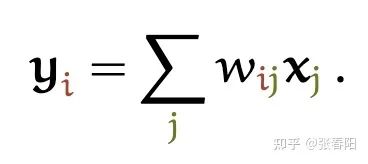
 代表整个序列的长度，并且  个权重的相加之和等于1。值得一提的是，这里的  并不是一个需要神经网络学习的参数，它是来源于  和  的之间的计算的结果（这里  的计算发生了变化）。它们之间最简单的一种计算方式，就是使用点积的方式。

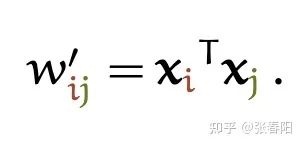
 和  是一对输入和输出。对于下一个输出的向量  ，我们有一个全新的输入序列和一个不同的权重值。

这个点积的输出的取值范围在负无穷和正无穷之间，所以我们要使用一个softmax把它映射到  之间，并且要确保它们对于整个序列而言的和为1。

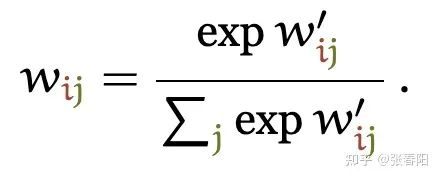
以上这些就是self-attention最基本的操作，其他的部分我们需要完整的Trasnformer才能够解释，这些我们会在后面的内容中说明。

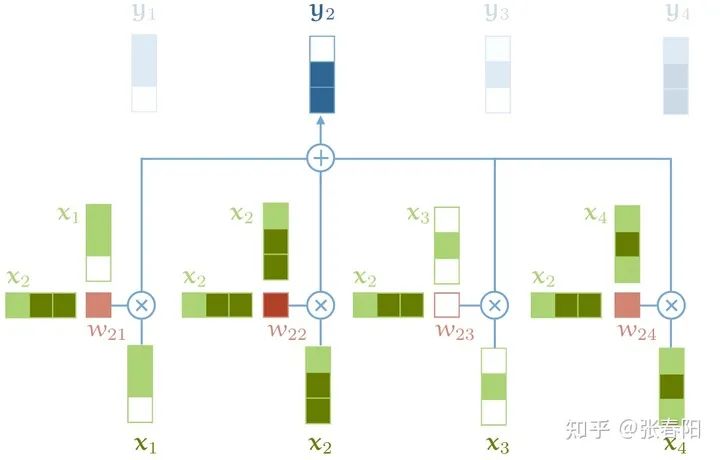
self-attention的基础操作，没有包含softmax操作

Attention 和 self-attention 的区别是什么 ？

这里有几个重要的区别，可以帮助大家更好的区分在不同任务中的使用方法：

1. 在神经网络中，通常来说你会有输入层（input），应用激活函数后的输出层（output），在RNN当中你会有状态（state）。如果attention (AT) 被应用在某一层的话，它更多的是被应用在输出或者是状态层上，而当我们使用self-attention（SA），这种注意力的机制更多的实在关注input上。
2. Attention (AT) 经常被应用在从编码器（encoder）转换到解码器（decoder）。比如说，解码器的神经元会接受一些AT从编码层生成的输入信息。在这种情况下，AT连接的是两个不同的组件（component），编码器和解码器。但是如果我们用SA，它就不是关注的两个组件，它只是在关注你应用的那一个组件。那这里他就不会去关注解码器了，就比如说在Bert中，使用的情况，我们就没有解码器。
3. SA可以在一个模型当中被多次的、独立的使用（比如说在Transformer中，使用了18次；在Bert当中使用12次）。但是，AT在一个模型当中经常只是被使用一次，并且起到连接两个组件的作用。
4. SA比较擅长在一个序列当中，寻找不同部分之间的关系。比如说，在词法分析的过程中，能够帮助去理解不同词之间的关系。AT却更擅长寻找两个序列之间的关系，比如说在翻译任务当中，原始的文本和翻译后的文本。这里也要注意，在翻译任务重，SA也很擅长，比如说Transformer。
5. AT可以连接两种不同的模态，比如说图片和文字。SA更多的是被应用在同一种模态上，但是如果一定要使用SA来做的话，也可以将不同的模态组合成一个序列，再使用SA。
6. 对我来说，大部分情况，SA这种结构更加的general，在很多任务作为降维、特征表示、特征交叉等功能尝试着应用，很多时候效果都不错。

Self-attention 为什么能 work ？

上面描述的方法看起来似乎很简单，但是它为什么能够work呢？为了能够建立起直观的感受，让我们来看看一种标准的推荐电影的方法，看看是否能得到一些启发。

假设你正在运营一家在线看电影的网站，你有一些电影和一些用户，你想要把合适的电影推荐给你的用户。你该怎么办呢？

一种方法是这样的，给你的电影手动的创建一些特征(feature)，比如说这部电影关于爱情的部分有多少，关于动作的部分有多少；然后我们再去对用户的特征进行分析，比如说用户A对于爱情电影的喜爱程度有多少，对动作电影的喜爱程度有多少。如果我们按照上述方式构建了用户和电影的两个矩阵，那么它们的点积就会给你一个分数，这个分数就代表了用户对于某种电影的喜爱程度。

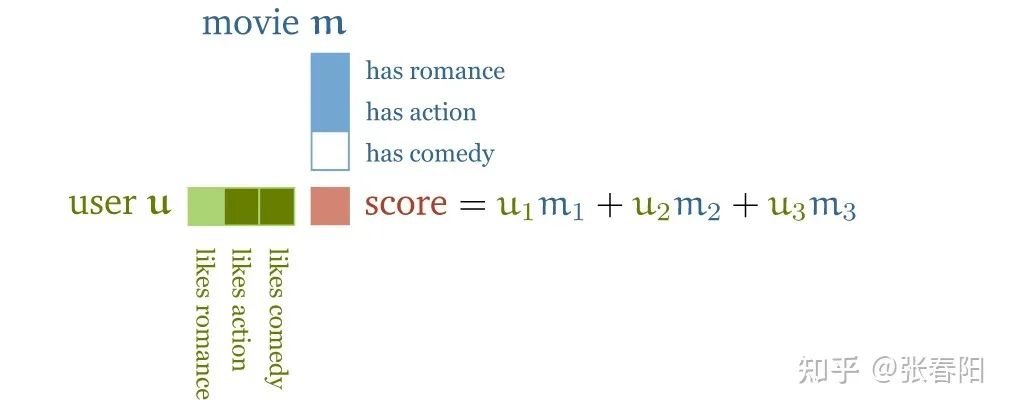
通过上面的这种计算方式，我们就能够得到一些score值。这些值有正数也有负数。比如说，电影是一部关于爱情的电影，并且用户也很喜欢爱情电影，那么这个分值就是一个正数；如果电影是关于爱情的，但是用户却不喜欢爱情电影，那么这个分值就会是一个负值。

还有，这个分值的大小也表示了在某个属性上，它的程度是多大：比如说某一部电影，可能它的内容中只有一点点是关于爱情的，那么它的这个值就会很小；或者说有个用户他不是很喜欢爱情电影，那么这个值的绝对值就会很大，说明他对这种电影的偏见是很大的。

显而易见，上面说的这种方法在现实中是很难实现的。我们很难去人工标注上千万的电影的特征，和用户喜欢哪种类型的电影的分值。

那么，我们有没有一种方法去通过问一小部分人，通过收集他们对电影的喜好，来通过一些算法来优化找出用户对于电影喜爱程度这个模型的参数呢？当然是有的，那就是FM算法，这个不是调频多少多少兆赫的那个FM，而是Factorization Machine。这个算法就是能通过左边的这个用户-电影矩阵，找到用户对于不同特征的喜好程度。

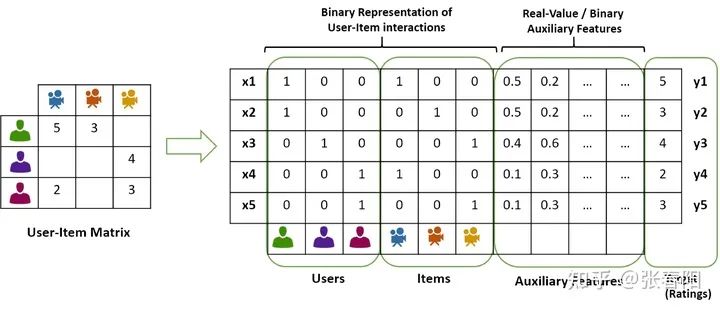
上面右边的矩阵是怎么来的呢？我们把上面的这个问题稍微的简化以下，只看成是一个和用户和物品两个维度相关的task，那其实我们就可以通过估计两个矩阵的点乘的形式，来对原有的矩阵表示。这两个向量中表示的就分别是用户的embedding和电影的embedding。我们反过来思考下，这种办法的核心思想就是是通过两个低维小矩阵（一个代表用户embedding矩阵，一个代表物品embedding矩阵）的点乘计算，来模拟真实用户点击或评分产生的大的协同信息稀疏矩阵，本质上是编码了用户和物品协同信息的降维模型。

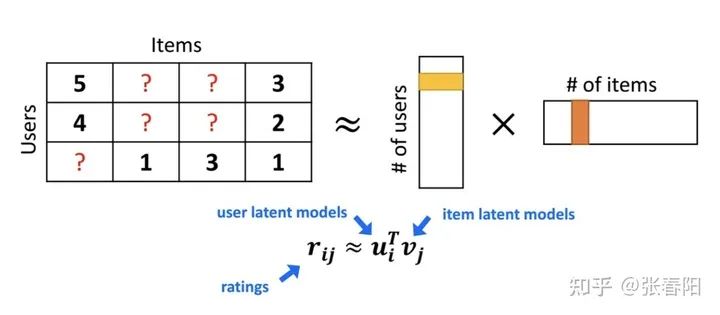
当我们想要看，某个用户对于某个电影的喜好程度时，只需要用他们的embedding相乘，就能得到相应的score了。

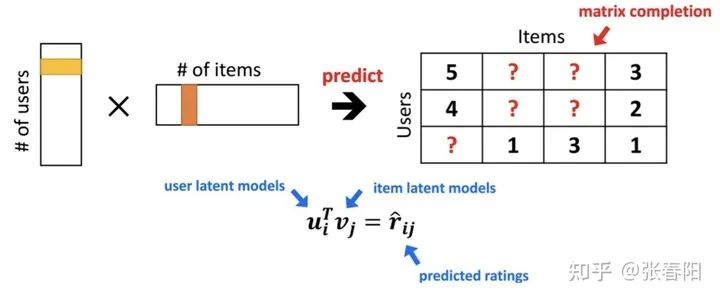
虽然，我们这里的两个embedding并没有直接的告诉我们，里面每个维度的参数的含义是什么，但是当你按照这种方法求的最后的参数的时候，这些参数都能够描述某种有实际含义的特征上。

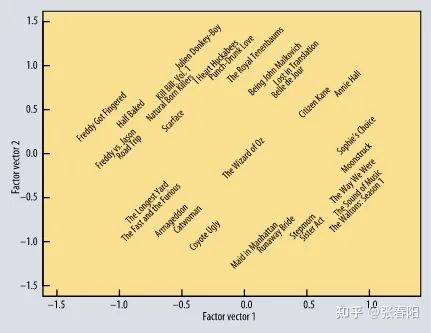
上面的这个过程，就和我们使用下面这个公式来表示attention的想法是一致的。

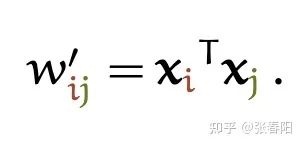
以上这些就是self-attention中为什么使用点乘的方法并且能work的原因了。那再让我们看一个在自然语言处理中使用self-attention的例子。为了应用self-attention，我们给每一个在词表中的单词  一个embeding向量  (这个是我们通过一些NLP方法学习到的)。这也是我们在序列模型中常见的embeding layer。它会把单词  转换成向量的形式

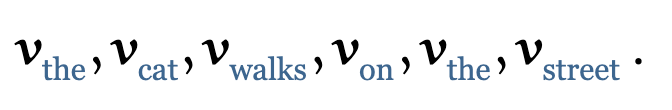
如果我们对这些向量序列进行self-attention的处理，那么就会生成一个新的向量序列

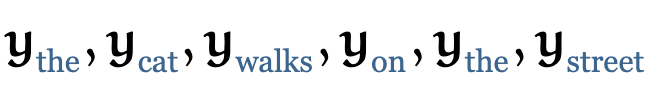
这其中  就是所有在第一个序列中的embedding向量的加权和，权重值就是  的点积。

上文中我们也提到了，  是我们学习到的embedding向量，它是  这个单词向量化的表示。在大部分的场景中，  这个单词和句子中的其他单词没有很强的相关性，因此，我们就会期待  和其他单词的点积结果应该比较小或者是一个负值。那再看 这个单词，为了能够解释这个单词，我们希望能够知道是谁在  ，那在这句话当中，  和  的点积就应该有一个比较大的正的值。

以上这些，就是在self-attention背后一些直觉上的含义。点积操作很好的表示了输入语句中两个向量之间的相关性。

在我们继续下面的内容之前，非常有必要做一个小的总结。

• 到目前为止，我们还没有用到需要学习的参数。基础的self-attention实际上完全取决于我们创建的输入序列，上游的embeding layer驱动着self-attention学习对于文本语义的向量表示。
• Self-attention看到的序列只是一个集合(set)，不是一个序列，它并没有顺序。如果我们重新排列集合，输出的序列也是一样的。后面我们要使用一些方法来缓和这种没有顺序所带来的信息的缺失。但是值得一提的是，self-attention本身是忽略序列的自然输入顺序的。
  
  

怎么用 Pytorch 实现self-attention ？

我不能实现的，也是我没有理解的。
-- 费曼

所以，我们将一起从头开始写一个self-attention。我们这里将会使用Pytorch来实现。

一个简单的实现方法就是循环所有的向量，去计算出权重和输出，但是这样的方法明显太慢了。所以我们要做的第一件事就是怎么使用矩阵乘法的形式来表达self-attention。

我们首先来表示输入，一个  维的由  个向量组成的序列构成的矩阵  。包含一个batch的参数  ，我们会得倒一个维度为  的张量。

所有的点积的结果  也构成一个矩阵，我们可以简单的使用  乘以它的转置得到。

import torchimport torch.nn.functional as F
# assume we have some tensor x with size (b, t, k)x = ...
raw_weights = torch.bmm(x, x.transpose(1, 2))# - torch.bmm is a batched matrix multiplication. It #   applies matrix multiplication over batches of #   matrices.

然后我们把权重值  转换成正值并且确保它们的和为1，我们使用一个row-wise的softmax。

weights = F.softmax(raw_weights, dim=2)

最后，我们计算输出的序列，我们只需要使用权重乘以矩阵  。这样我们就得到了维度为的矩阵  。

y = torch.bmm(weights, x)
以上，经过两个简单的矩阵乘法和一个softmax，我们就得到了self-attention。

实际在Transformer的实现过程中，作者使用了三个tricks。下面就来一个个的聊一聊这几个tricks。

1) Queries, keys and values

我们回顾以下上面所说道的self-attention的内容，上面我们也提到了，在这样一个模型当中，是没有使用到可以学习参数的，那我们能不能使用一些参数，来让整个结构更加的flexable。就是由于这样的想法，诞生了query，key和value这些参数。

为了能够更清楚的说明，我们使用图片来稍微回顾下，之前讲过的self-attention，如下图。

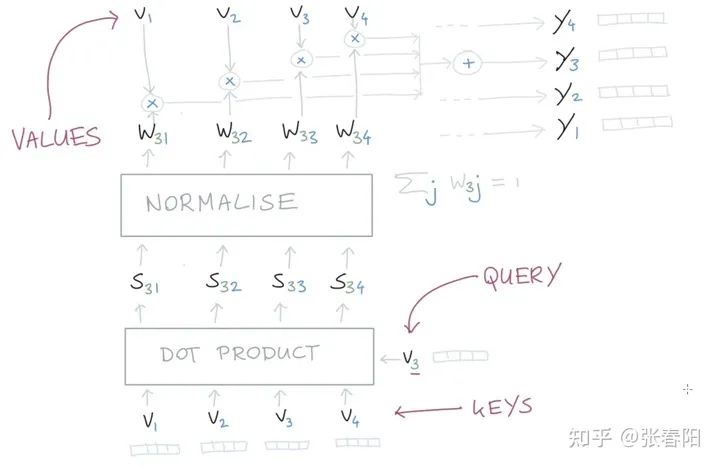
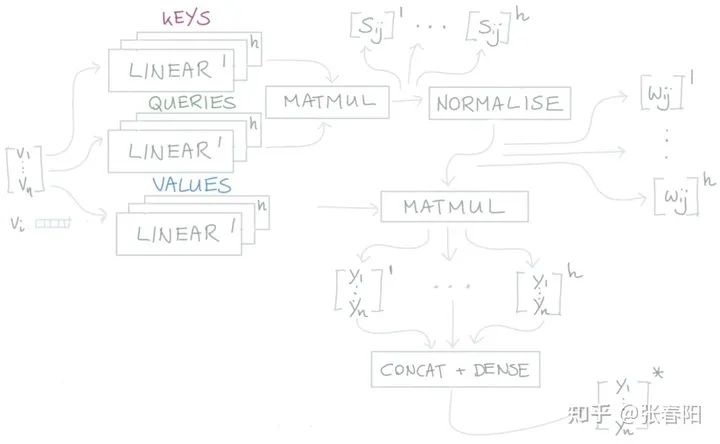
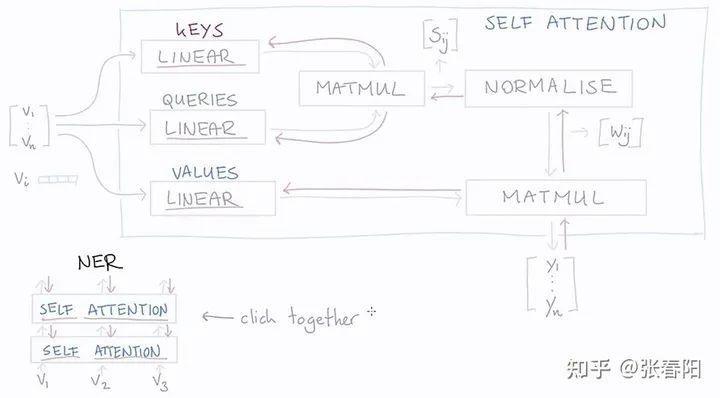
在整个计算的过程中，大家会发现，我们使用了三次向量  这个文本的表示来做计算，那在Transformer中，就是把这几个变量参数化，使用可以学习的参数来替代，这里我们分别使用key、query和value三个可学习的向量来表示，这里记为 ，  ， ，通过下面的计算，来得到re-weighting的向量  。

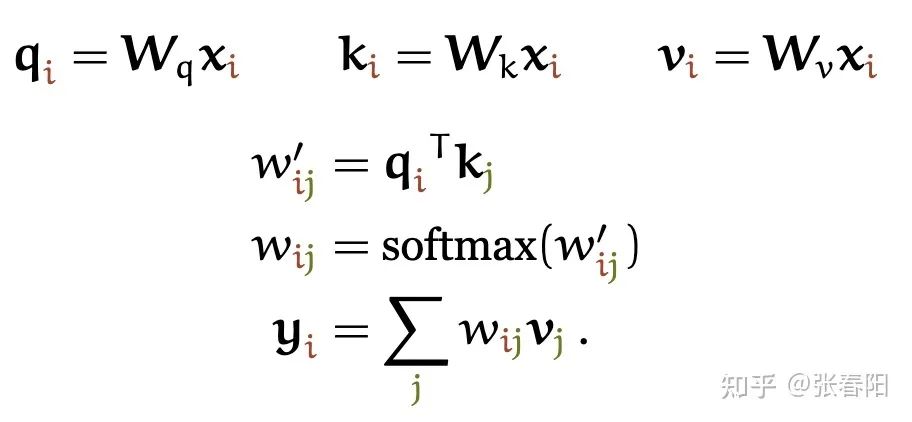
通过图形化的方法表示如下：

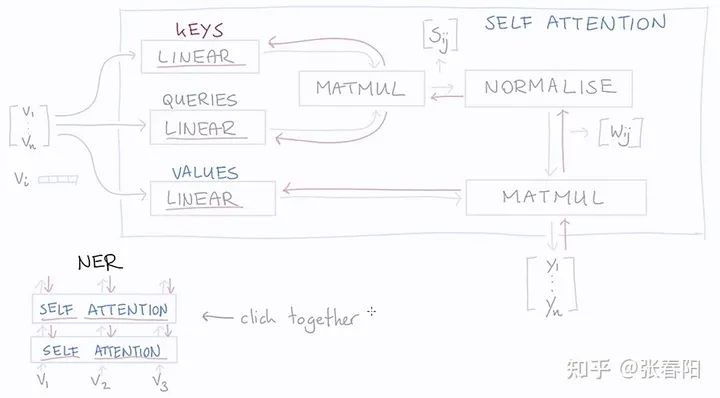
Linear层是一个没有bias的全连接层，其实就是一个点乘。红色的箭头表示的是反向传播的过程。通过方向传播，key，query，value就能够学习到一个合理的表示。那么这里面key，queue，value分别学习到的是什么呢？这个可能并没有一个官方的解释，但是通过这三个名称的命名方式，我们可以大致的猜测。

这种命名的方式来源于搜索领域，假设我们有一个key-value形式的数据集，就比如说是我们知乎的文章，key就是文章的标题，value就是我们文章的内容，那这个搜索系统就是希望，能够在我们输入一个query的时候，能够唯一返回一篇最我们最想要的文章。那在self-attention中其实是对这个task做了一些退化的处理，我们优化并不是返回一篇文章，而是返回所有的文章value，并且使用key和query计算出来的相关权重，来找到一篇得分最高的文章。

2) 缩放点积的值(Scaling the dot product)

Softmax 函数对非常大的输入很敏感。这会使得梯度的传播出现为问题(kill the gradient)，并且会导致学习的速度下降(slow down learning)，甚至会导致学习的停止。那如果我们使用  来对输入的向量做缩放，就能够防止进入到softmax的函数增长过大：

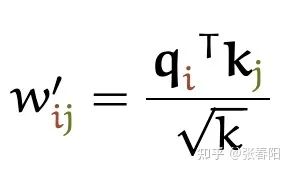
这里分母为什么要使用  呢？我们想象一下，当我们有一个所有的值都为  的在  空间内的值。那它的欧式距离就为  。除以其实就是在除以向量平均的增长长度。

3) Multi-head attention

最后，我们必须要知道的是，在真实的语言环境中，每一个词和不同的词，都有不同的关系。我们考虑下面这个例子，  。我们可以看到  和不同的部分有不同的关系。首先，  表示谁在进行  的动作，  表达被  的东西是什么，  表示谁在接受东西。我们就可以用不同的self-attention mechanism来补货这些不同的关系。如下图：

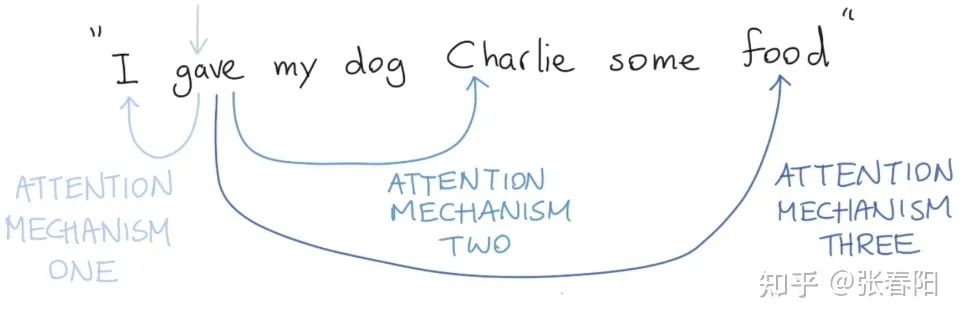
如果我们只进行single self-attention，所有的信息都会被加和到一起。如果是  给   ，那么我们得到的  就是一样的了，但是其实意思应发生了改变。

所以，我们可以通过增加多个self-attention这样的结构，来给self attention更强的辨别能力，我们就有了更多个  的矩阵  ，那我们把这些不同的self-attention就叫做attention head。

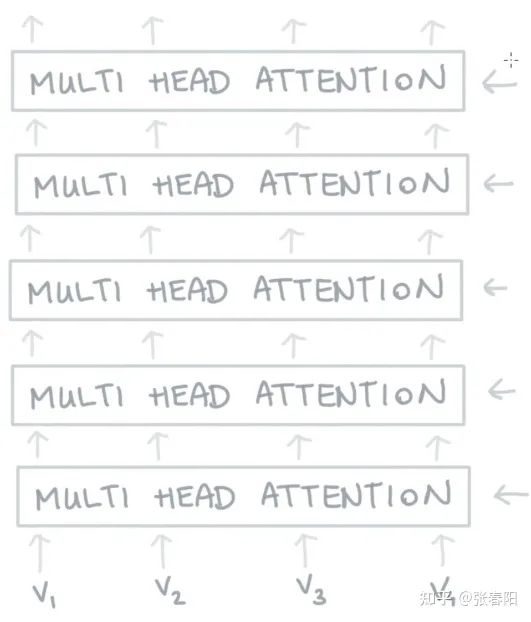
对于输入  每一个attention head都会生成一个向量  。我们把这些向量进行concat操作，并且把concat的结果传递给一个全连接层，使得向量的维度重新回到k。这样我们就得到了一个表示能力更强的向量。那应用了multi-head后的attention结构就变成了下图这样子：

有了这个结构，我们就可以把多个multi-head attention结构堆叠起来，从而得到更加强大的能力。

Narrow and wide self-attention
通常，我们有两种方式来实现multi-head的self-attention。默认的做法是我们会把embedding的向量  切割成块，比如说我们有一个256大小的embedding vector，并且我们使用8个attention head，那么我们会把这vector切割成8个维度大小为32的块。对于每一块，我们生成它的queries，keys和values，它们每一个的size都是32，那么也就意味着我们矩阵  的大小都是  。
那还有一种方法是，我们可以让矩阵的大小都是  ，并且把每一个attention head都应用到全部的256维大小的向量上。第一种方法的速度会更快，并且能够更节省内存，第二种方法能够得到更好的结果(同时也花费更多的时间和内存)。这两种方法分别叫做narrow and wide self-attention。

怎么用 Pytorch/Tensorflow2.0 实现在 Transfomer 中的self-attention ？

实现Transformer中的self-attention过程，我们一共有8个步骤：

1. 准备输入
2. 初始化参数
3. 获取key，query和value
4. 给input1计算attention score
5. 计算softmax
6. 给value乘上score
7. 给value加权求和获取output1
8. 重复步骤4-7，获取output2，output3

1 准备输入

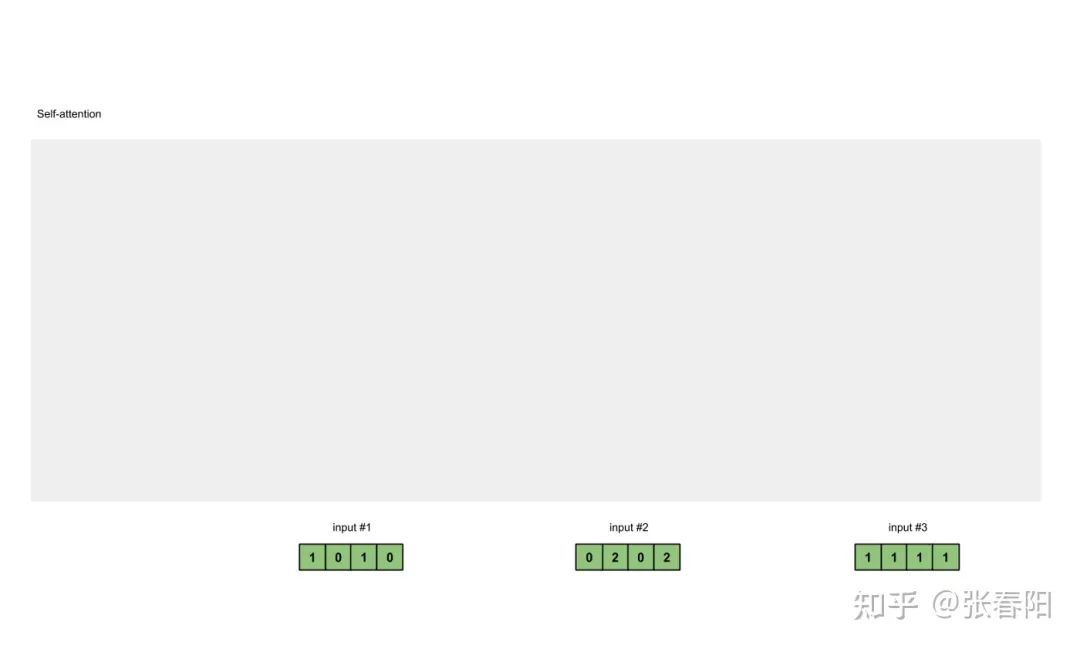
为了简单起见，我们使用3个输入，每个输入都是一个4维的向量。

Input 1: [1, 0, 1, 0] Input 2: [0, 2, 0, 2]Input 3: [1, 1, 1, 1]

2 初始化参数

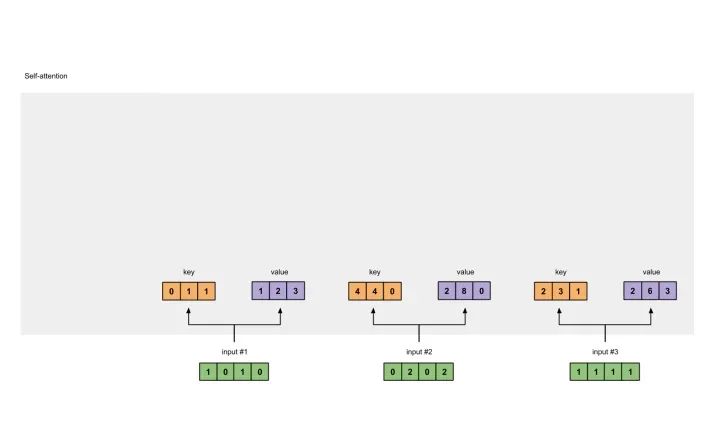
每一个输入都有三个表示，分别为key（橙黄色）query（红色）value（紫色）。比如说，每一个表示我们希望是一个3维的向量。由于输入是4维，所以我们的参数矩阵为  维。

后面我们会看到，value的维度，同样也是我们输出的维度。

为了能够获取这些表示，每一个输入（绿色）要和key，query和value相乘，在我们例子中，我们使用如下的方式初始化这些参数。

key的参数：

[[0, 0, 1], [1, 1, 0], [0, 1, 0], [1, 1, 0]]
query的参数：

[[1, 0, 1], [1, 0, 0], [0, 0, 1], [0, 1, 1]]
value的参数：

[[0, 2, 0], [0, 3, 0], [1, 0, 3], [1, 1, 0]]

通常在神经网络的初始化过程中，这些参数都是比较小的，一般会在_Gaussian,
Xavier and Kaiming distributions随机采样完成。_

3 获取key，query和value

现在我们有了三个参数，现在就让我们来获取实际上的key，query和value。

对于input1的key的表示为：

               [0, 0, 1][1, 0, 1, 0] x [1, 1, 0] = [0, 1, 1]               [0, 1, 0]               [1, 1, 0]

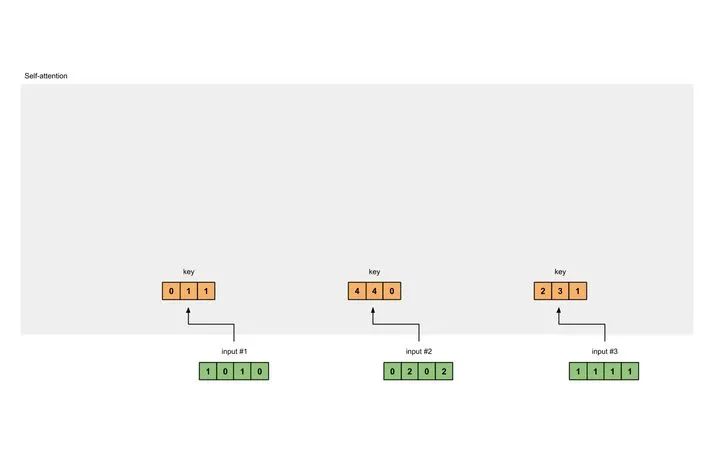
使用相同的参数获取input2的key的表示：

               [0, 0, 1][0, 2, 0, 2] x [1, 1, 0] = [4, 4, 0]               [0, 1, 0]               [1, 1, 0]

使用参数获取input3的key的表示：

               [0, 0, 1][1, 1, 1, 1] x [1, 1, 0] = [2, 3, 1]               [0, 1, 0]               [1, 1, 0]

那使用向量化的表示为：

               [0, 0, 1][1, 0, 1, 0]   [1, 1, 0]   [0, 1, 1][0, 2, 0, 2] x [0, 1, 0] = [4, 4, 0][1, 1, 1, 1]   [1, 1, 0]   [2, 3, 1]

让我们对value做相同的事情。

               [0, 2, 0][1, 0, 1, 0]   [0, 3, 0]   [1, 2, 3] [0, 2, 0, 2] x [1, 0, 3] = [2, 8, 0][1, 1, 1, 1]   [1, 1, 0]   [2, 6, 3]

query也是一样的。

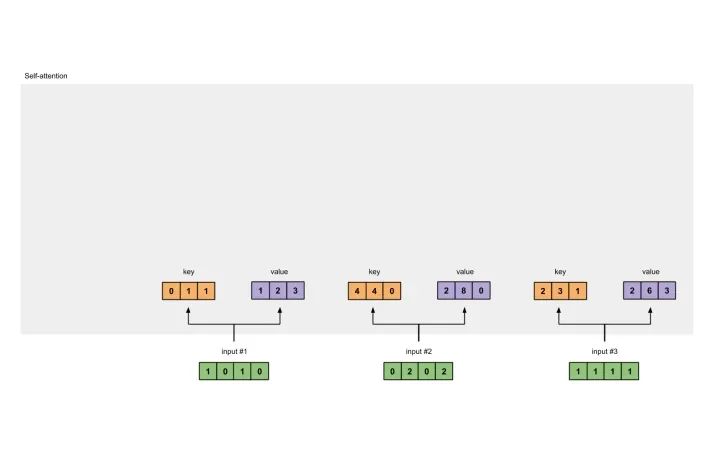
               [1, 0, 1][1, 0, 1, 0]   [1, 0, 0]   [1, 0, 2][0, 2, 0, 2] x [0, 0, 1] = [2, 2, 2][1, 1, 1, 1]   [0, 1, 1]   [2, 1, 3]

在我们实际的应用中，有可能会在点乘后，加上一个bias的向量。

4 给input1计算attention score

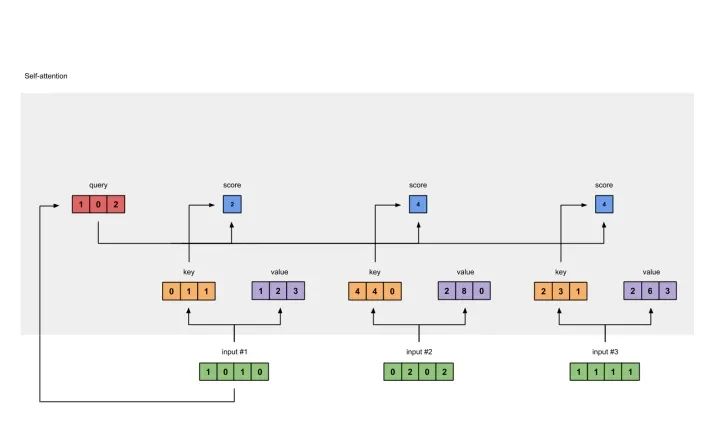
为了获取input1的attention score，我们使用点乘来处理所有的key和query，包括它自己的key和value。这样我们就能够得到3个key的表示（因为我们有3个输入），我们就获得了3个attention score（蓝色）。

            [0, 4, 2][1, 0, 2] x [1, 4, 3] = [2, 4, 4]            [1, 0, 1]

这里我们需要注意一下，这里我们只有input1的例子。后面，我们会对其他的输入的query做相同的操作。

5 计算softmax

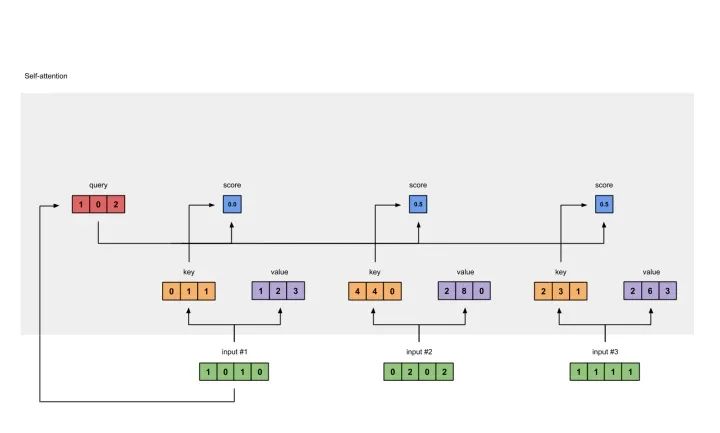
给attention score应用softmax。

softmax([2, 4, 4]) = [0.0, 0.5, 0.5]

6 给value乘上score

使用经过softmax后的attention score乘以它对应的value值（紫色），这样我们就得到了3个weighted values（黄色）。

1: 0.0 * [1, 2, 3] = [0.0, 0.0, 0.0]2: 0.5 * [2, 8, 0] = [1.0, 4.0, 0.0]3: 0.5 * [2, 6, 3] = [1.0, 3.0, 1.5]

7 给value加权求和获取output1

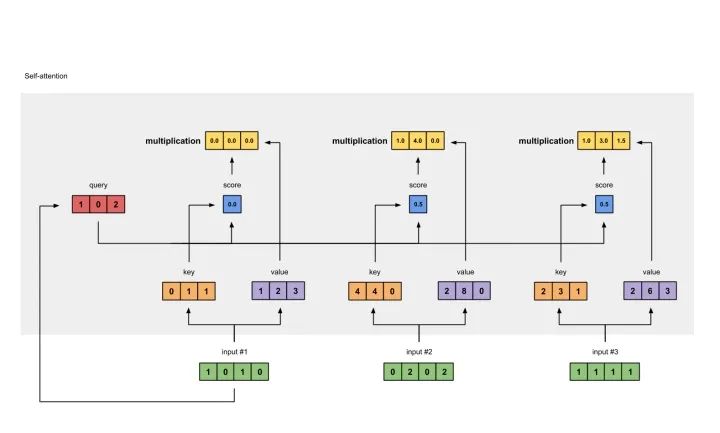
把所有的weighted values（黄色）进行element-wise的相加。

  [0.0, 0.0, 0.0]+ [1.0, 4.0, 0.0]+ [1.0, 3.0, 1.5]-----------------= [2.0, 7.0, 1.5]

得到结果向量[2.0, 7.0, 1.5]（深绿色）就是ouput1的和其他key交互的query representation。

8 重复步骤4-7，获取output2，output3

现在，我们已经完成output1的全部计算，我们要对input2和input3也重复的完成步骤4～7的计算。这相信大家自己是可以实现的。

实现的代码，我给大家准备了jupyter notebook，大家可以clone下面的repo，自己一步步的完成代码的调试，加深对于self-attention的理解。

https://github.com/BSlience/transformer-all-in-onegithub.com

Transformer 模型来源于Google发表的一篇论文 “Attention Is All You Need”，截止到我查询的时候，这篇文章已经有17000+的引用量，可见这篇文章的影响力。希望大家能在有一些了解的基础上，能够自己读一下这篇文章。

https://arxiv.org/pdf/1706.03762.pdfarxiv.org

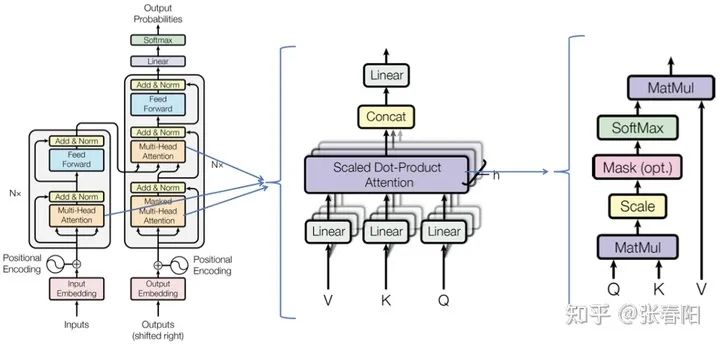
上面这张图片是论文原文中的图片，我把他们放在了一起。这几个模型分别代表了 Transformer 在翻译任务中的应用（左），Multi-Head Attention（中），self-attention（右）。在前面的文章中，我们已经讲解过 self-attetnion（右），这里和我们之前讲解过的稍有不同的是多了一个粉色的方框 Mask（opt），这个是用来左Mask任务的，括号中的opt表示是一个可选项，本篇先不提，后面我们再细说；也讲解了 Multi-Head Attention（中），多头的注意力机制；本篇文章，我们把重点集中在最左侧的图片，来看看 Transformer 结构。

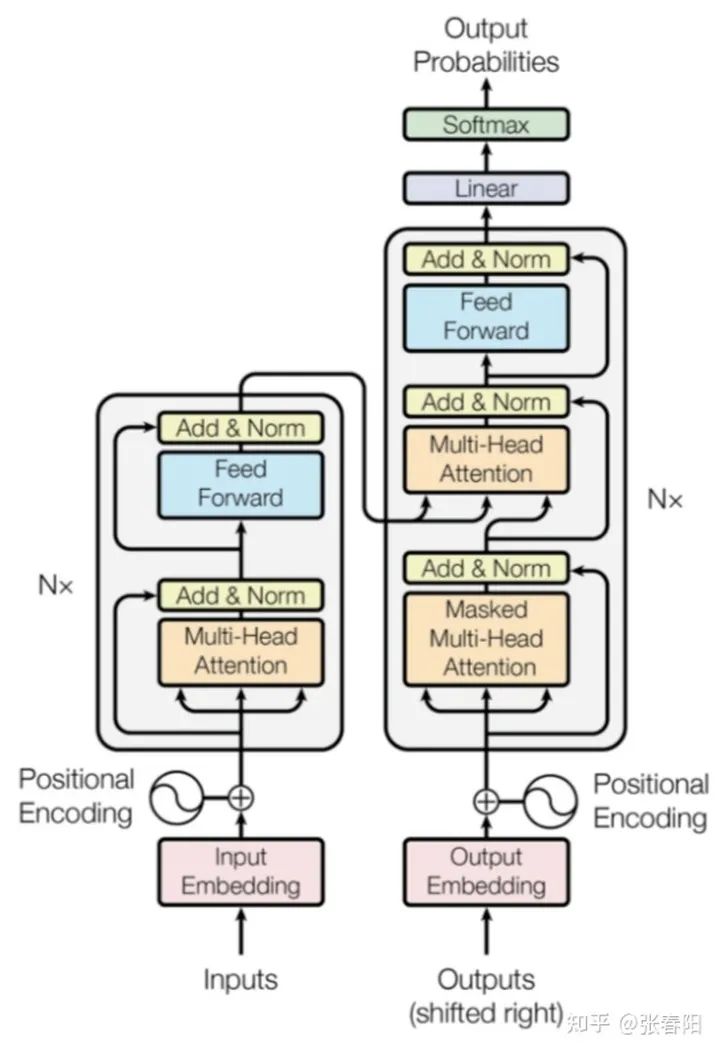
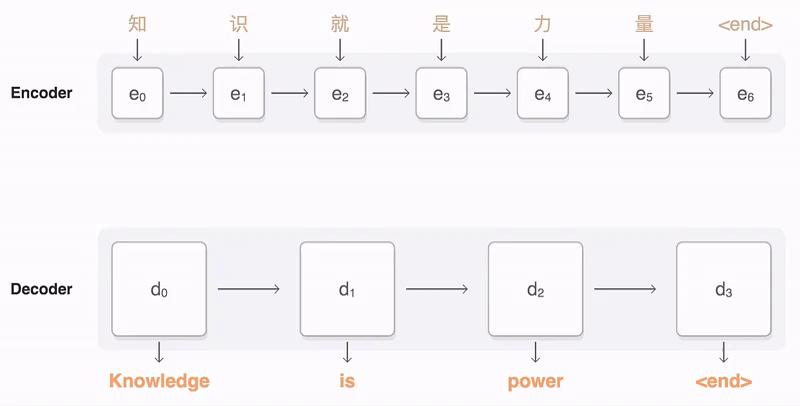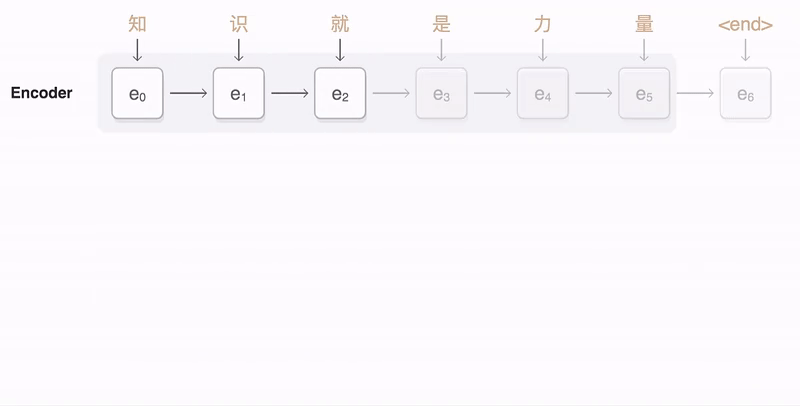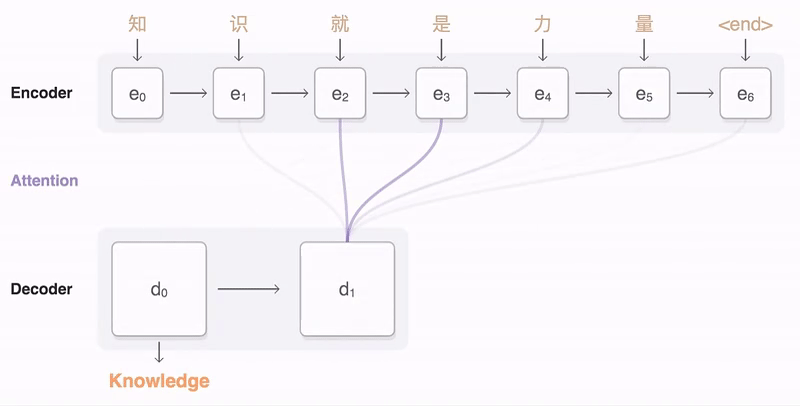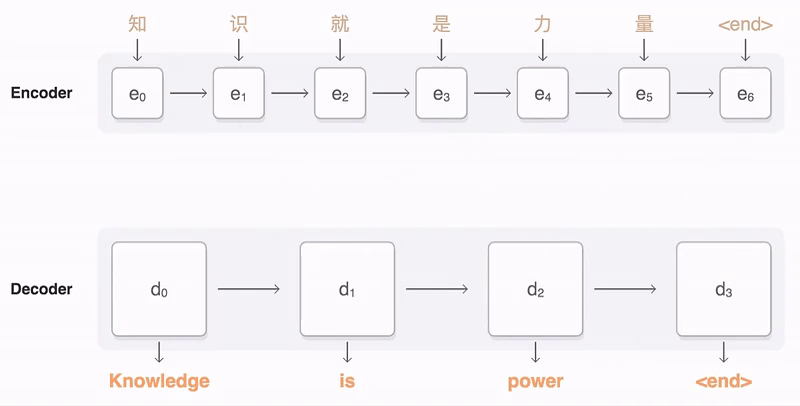
我们来把这幅图放大来看，这个模型结构分为左右两个部分，因为原文中是用Transtormer来做翻译任务的，大家可能知道通常我们做翻译任务的时候，都使用 Encoder-Decoder 的架构来做。这里面的左侧对应着 Encoder ，右侧就是 Decoder 。Encoder 本质的目的就是对 input 生成一种中间表示，Decoder目的就是对这种中间表示做解码，生成目标语言的ouput。大家会发现两边的结构基本上是一致的，为了着重的研究Transformer结构，我们把视线聚焦在Encoder的部分。

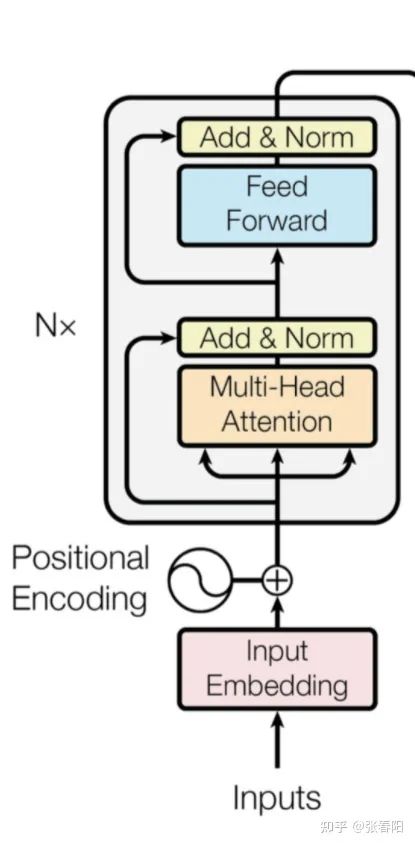
大家会在图中看到，这里有个  的符号，这表示了右侧的结构可以被  次堆叠，这就像是我们在使用神经网络的时候，可以  次堆叠 layer 一样，通常我们把这样的一种由多个 layer 组成的模块叫做 block，这种 block 就是一种比 layer 更大规模的可复用单元。那么，接下来我们把重点放到 Transformer Block 上。

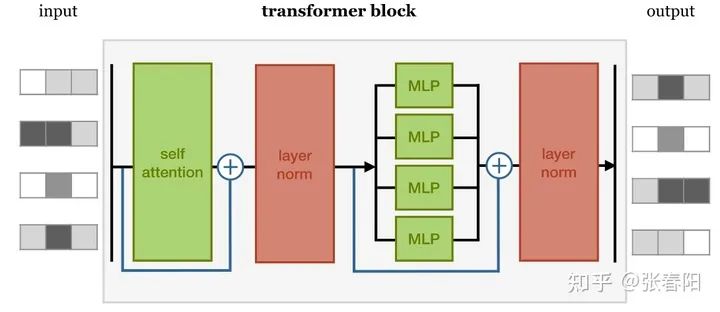
在这样一个block中，是由几个重要的组件构成的：

1. self-attention layer
2. normalization layer
3. feed forward layer
4. another normalization layer

在这样四个组件中的两个 normalization layer 之前，使用了残差网络（Residula connections）进行了连接。实际上，这几个组件之间的顺序并没有被完全的定死，这里面最重要的事情是，要联合使用 self-attention 和 feed forward layer，并且要在它们之间增加normalization 和 residual connections。

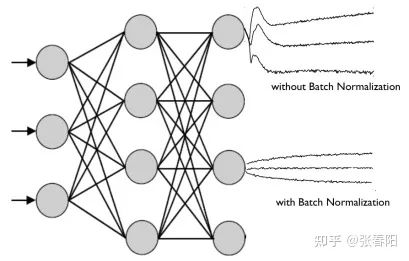
Normaliztion 和 residual connections 是我们经常使用的，帮助加快深度神经网络训练速度和准确率的 tricks。

这里我们可以先看看使用 Pytorch 实现这样一个 block 是什么样子的。

class TransformerBlock(nn.Module):  def __init__(self, k, heads):    super().__init__()
    self.attention = SelfAttention(k, heads=heads)
    self.norm1 = nn.LayerNorm(k)    self.norm2 = nn.LayerNorm(k)
    self.ff = nn.Sequential(      nn.Linear(k, 4 * k),      nn.ReLU(),      nn.Linear(4 * k, k))
  def forward(self, x):    attended = self.attention(x)    x = self.norm1(attended + x)        fedforward = self.ff(x)    return self.norm2(fedforward + x)

我们这里主观的选择4倍输入大小作为我们 feedforward 层的维度，这个值使用的越小就越节省内存，但是相应的表示性也会变弱；但是，最小也应该大于我们输入的维度。

怎么捕获序列中的顺序信息呢 ？

通过使用 Transformer 我们可以得到一个对于输入信息的 embedding vector，但是这里大家可能也会发现，我们并没有利用好序列的输入顺序。比如说  和  ，它们得到的 vector 是一样的。显然，这并不是希望看到的。所以，我们要给模型增加捕获序列顺序的能力。我们应该怎么做呢？

办法也很简单，我们创建一个和输入序列等长的新序列，这个序列里包含序列中的顺序信息，我们把这个序列和原有序列进行相加，从而得到输入到 Transformer 的序列。那应该怎样表示序列中的位置信息呢？

这里我们有两种方法：

• position embeddings

我们简单的 embed 位置信息，就像我们对待每一个输入一样。比如说我们之前对每个单词 创建一个 vector  ，那我们也对每一个位置生成一个向量  。然后我们使用模型的学习能力来学习到这些位置的 vector。但是这种方法会存在一个问题，那就是我们需要在训练的过程中让模型见过所有的需要在预测阶段使用的位置 vector，否则模型就不知道相应位置的 vector。

• position encodings

position encoding的方法其实和 position embedding 的方法很相似，我们都是希望能够通过一个位置的 vector 来表示位置的信息，让模型学习到这个信息。但是，这里稍有不同的是，encoding 的方法是由我们选择一个 function 来生成每个位置的 vector 的，并且让模型网络去找出该如何去理解这些 encoding vector。这样做的好处是，对于一个选择的比较好的function，网络模型能够处理那些在训练阶段没有见过的序列位置 vector（虽然这也并不是说这些没见过的位置 vector 一定能够表现的很好，但是好在是我们可以有比较直接的方法来测试他们）。这种方法也是 Transformer 的作者选择的方法，让我们看看作者是怎么设计这个 function 的。

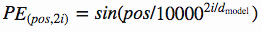
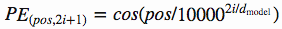
作者使用上面的两个 functions 来生成一个2维的矩阵常量，  表示在序列中的顺序，  表示序列中数据 vector 的维度，  表示输出的维度大小，如下图所示：

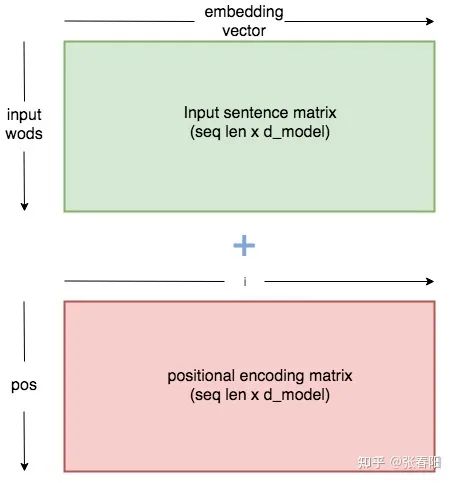
这里我给出一个使用 Pytorch 实现的 PositionEncoder 的代码：

class PositionalEncoder(nn.Module):    def __init__(self, d_model, max_seq_len = 80):        super().__init__()        self.d_model = d_model                # 根据pos和i创建一个常量pe矩阵        pe = torch.zeros(max_seq_len, d_model)        for pos in range(max_seq_len):            for i in range(0, d_model, 2):                pe[pos, i] = \                math.sin(pos / (10000 ** ((2 * i)/d_model)))                pe[pos, i + 1] = \                math.cos(pos / (10000 ** ((2 * (i + 1))/d_model)))                        pe = pe.unsqueeze(0)        self.register_buffer('pe', pe)     def forward(self, x):        # 让 embeddings vector 相对大一些        x = x * math.sqrt(self.d_model)        # 增加位置常量到 embedding 中        seq_len = x.size(1)        x = x + Variable(self.pe[:,:seq_len], \                         requires_grad=False).cuda()        return x

上面的这个模块中，我们在数据的 embedding vector 增加了 position encoding 的信息。

让 embeddings vector 在增加 postion encoing 之前相对大一些的操作，主要是为了让position encoding 相对的小，这样会让原来的 embedding vector 中的信息在和 position encoding 的信息相加时不至于丢失掉。

怎么用 Pytorch 实现一个完整的 Transformer 模型？

1. Tokenize
2. Input Embedding
3. Positional Encoder
4. Transformer Block
5. Encoder
6. Decoder
7. Transformer

1 Tokenize

首先，我们要对输入的语句做分词，这里我使用 spacy 来完成这件事，你也可以选择你喜欢的工具来做。

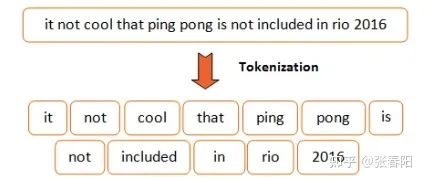
class Tokenize(object):        def __init__(self, lang):        self.nlp = importlib.import_module(lang).load()                def tokenizer(self, sentence):        sentence = re.sub(        r"[\*\"“”\n\\…\+\-\/\=\(\)‘•:\[\]\|’\!;]", " ", str(sentence))        sentence = re.sub(r"[ ]+", " ", sentence)        sentence = re.sub(r"\!+", "!", sentence)        sentence = re.sub(r"\,+", ",", sentence)        sentence = re.sub(r"\?+", "?", sentence)        sentence = sentence.lower()        return [tok.text for tok in self.nlp.tokenizer(sentence) if tok.text != " "]

2 Input Embedding

Token Embedding

给语句分词后，我们就得到了一个个的 token，我们之前有说过，要对这些token做向量化的表示，这里我们使用 pytorch 中torch.nn.Embedding 让模型学习到这些向量。

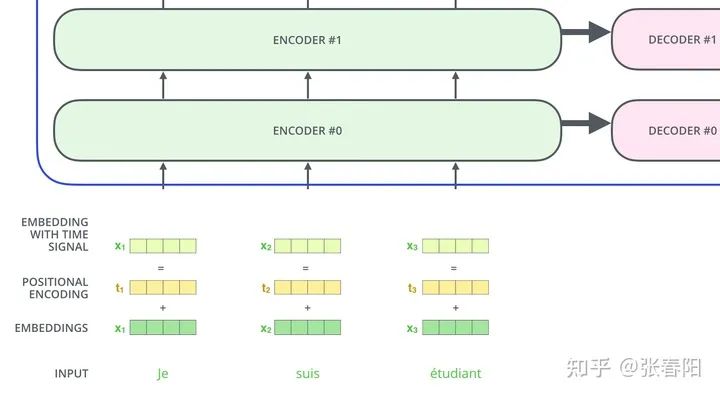
class Embedding(nn.Module):        def __init__(self, vocab_size, d_model):        super().__init__()        self.d_model = d_model        self.embed = nn.Embedding(vocab_size, d_model)            def forward(self, x):        return self.embed(x)

Positional Encoder

前文中，我们有说过，要把 token 在句子中的顺序也加入到模型中，让模型进行学习。这里我们使用的是 position encodings 的方法。

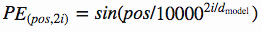
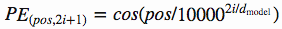
class PositionalEncoder(nn.Module):
    def __init__(self, d_model, max_seq_len = 80):        super().__init__()        self.d_model = d_model                # 根据pos和i创建一个常量pe矩阵        pe = torch.zeros(max_seq_len, d_model)        for pos in range(max_seq_len):            for i in range(0, d_model, 2):                pe[pos, i] = \                math.sin(pos / (10000 ** ((2 * i)/d_model)))                pe[pos, i + 1] = \                math.cos(pos / (10000 ** ((2 * (i + 1))/d_model)))                        pe = pe.unsqueeze(0)        self.register_buffer('pe', pe)     def forward(self, x):        # 让 embeddings vector 相对大一些        x = x * math.sqrt(self.d_model)        # 增加位置常量到 embedding 中        seq_len = x.size(1)        x = x + Variable(self.pe[:,:seq_len], \                         requires_grad=False).cuda()        return x

3 Transformer Block

有了输入，我们接下来就要开始构建 Transformer Block 了，Transformer Block 主要是有以下4个部分构成的：

1. self-attention layer
2. normalization layer
3. feed forward layer
4. another normalization layer

它们之间使用残差网络进行连接，详细在上文同一个图下有描述，这里就不再赘述了。

Attention

def attention(q, k, v, d_k, mask=None, dropout=None):        scores = torch.matmul(q, k.transpose(-2, -1)) /  math.sqrt(d_k)        # mask掉那些为了padding长度增加的token，让其通过softmax计算后为0    if mask is not None:        mask = mask.unsqueeze(1)        scores = scores.masked_fill(mask == 0, -1e9)        scores = F.softmax(scores, dim=-1)        if dropout is not None:        scores = dropout(scores)            output = torch.matmul(scores, v)    return output

这个 attention 的代码中，使用 mask 的机制，这里主要的意思是因为在去给文本做 batch化的过程中，需要序列都是等长的，不足的部分需要 padding。但是这些 padding 的部分，我们并不想在计算的过程中起作用，所以使用 mask 机制，将这些值设置成一个非常大的负值，这样才能让 softmax 后的结果为0。关于 mask 机制，在 Transformer 中有 attention、encoder 和 decoder 中，有不同的应用，我会在后面的文章中进行解释。

MultiHead Attention

多头的注意力机制，用来识别数据之间的不同联系，前文中的第二篇也已经聊过了。

class MultiHeadAttention(nn.Module):        def __init__(self, heads, d_model, dropout = 0.1):        super().__init__()                self.d_model = d_model        self.d_k = d_model // heads        self.h = heads                self.q_linear = nn.Linear(d_model, d_model)        self.v_linear = nn.Linear(d_model, d_model)        self.k_linear = nn.Linear(d_model, d_model)                self.dropout = nn.Dropout(dropout)        self.out = nn.Linear(d_model, d_model)        def forward(self, q, k, v, mask=None):                bs = q.size(0)                # perform linear operation and split into N heads        k = self.k_linear(k).view(bs, -1, self.h, self.d_k)        q = self.q_linear(q).view(bs, -1, self.h, self.d_k)        v = self.v_linear(v).view(bs, -1, self.h, self.d_k)                # transpose to get dimensions bs * N * sl * d_model        k = k.transpose(1,2)        q = q.transpose(1,2)        v = v.transpose(1,2)                # calculate attention using function we will define next        scores = attention(q, k, v, self.d_k, mask, self.dropout)        # concatenate heads and put through final linear layer        concat = scores.transpose(1,2).contiguous()\        .view(bs, -1, self.d_model)        output = self.out(concat)            return output

Layer Norm

这里使用 Layer Norm 来使得梯度更加的平稳，关于为什么选择 Layer Norm 而不是选择其他的方法，有篇论文对此做了一些研究，Rethinking Batch Normalization in Transformers，对这个有兴趣的可以看看这篇文章。

https://arxiv.org/pdf/2003.07845.pdfarxiv.org

class NormLayer(nn.Module):        def __init__(self, d_model, eps = 1e-6):        super().__init__()            self.size = d_model                # 使用两个可以学习的参数来进行 normalisation        self.alpha = nn.Parameter(torch.ones(self.size))        self.bias = nn.Parameter(torch.zeros(self.size))                self.eps = eps        def forward(self, x):        norm = self.alpha * (x - x.mean(dim=-1, keepdim=True)) \        / (x.std(dim=-1, keepdim=True) + self.eps) + self.bias        return norm

Feed Forward Layer

class FeedForward(nn.Module):        def __init__(self, d_model, d_ff=2048, dropout = 0.1):        super().__init__()             # We set d_ff as a default to 2048        self.linear_1 = nn.Linear(d_model, d_ff)        self.dropout = nn.Dropout(dropout)        self.linear_2 = nn.Linear(d_ff, d_model)        def forward(self, x):        x = self.dropout(F.relu(self.linear_1(x)))        x = self.linear_2(x)

5 Encoder

Encoder 就是将上面讲解的内容，按照下图堆叠起来，完成将源编码到中间编码的转换。

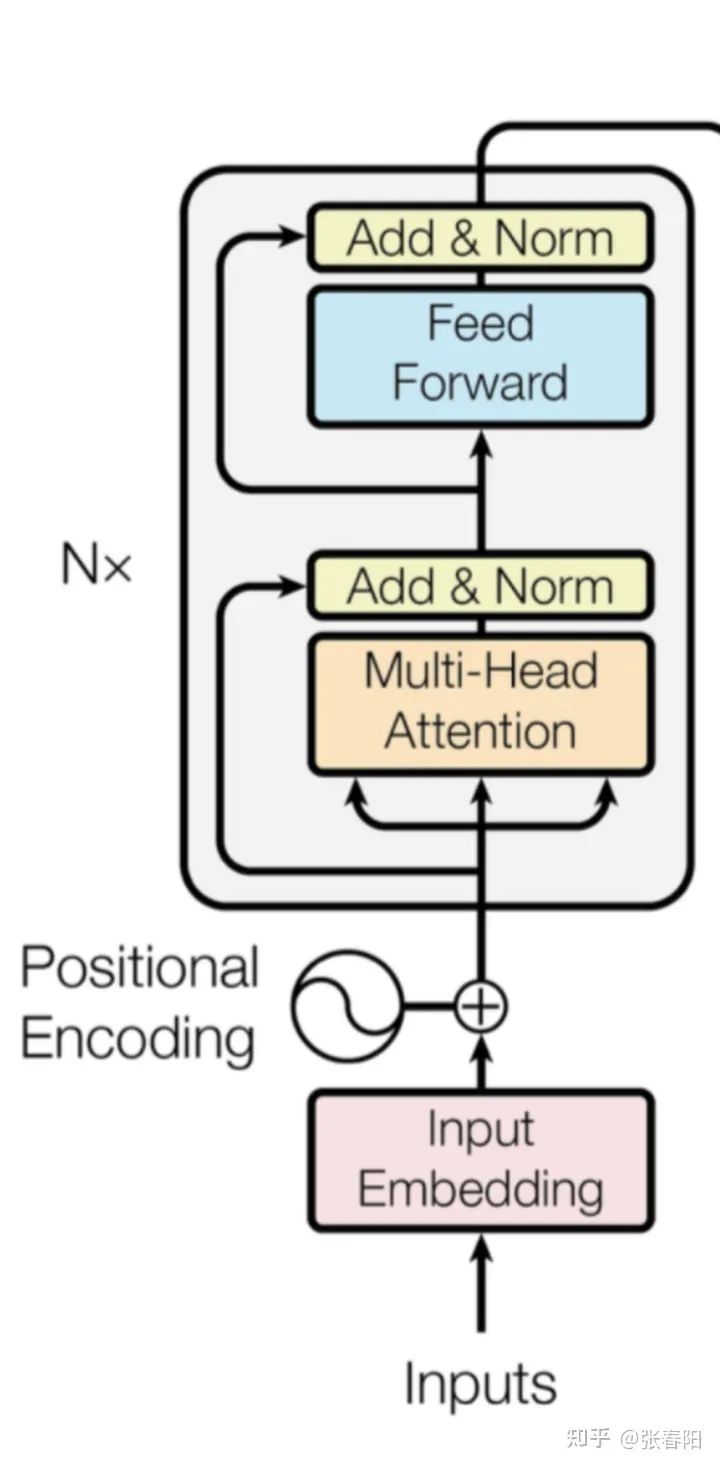
class EncoderLayer(nn.Module):
    def __init__(self, d_model, heads, dropout=0.1):        super().__init__()        self.norm_1 = Norm(d_model)        self.norm_2 = Norm(d_model)        self.attn = MultiHeadAttention(heads, d_model, dropout=dropout)        self.ff = FeedForward(d_model, dropout=dropout)        self.dropout_1 = nn.Dropout(dropout)        self.dropout_2 = nn.Dropout(dropout)            def forward(self, x, mask):        x2 = self.norm_1(x)        x = x + self.dropout_1(self.attn(x2,x2,x2,mask))        x2 = self.norm_2(x)        x = x + self.dropout_2(self.ff(x2))        return x

class Encoder(nn.Module):
    def __init__(self, vocab_size, d_model, N, heads, dropout):        super().__init__()        self.N = N        self.embed = Embedder(vocab_size, d_model)        self.pe = PositionalEncoder(d_model, dropout=dropout)        self.layers = get_clones(EncoderLayer(d_model, heads, dropout), N)        self.norm = Norm(d_model)
    def forward(self, src, mask):        x = self.embed(src)        x = self.pe(x)        for i in range(self.N):            x = self.layers[i](x, mask)        return self.norm(x)

6 Decoder

Decoder部分和 Encoder 的部分非常的相似，它主要是把 Encoder 生成的中间编码，转换为目标编码。后面我会在具体的任务中，来分析它和 Encoder 的不同。

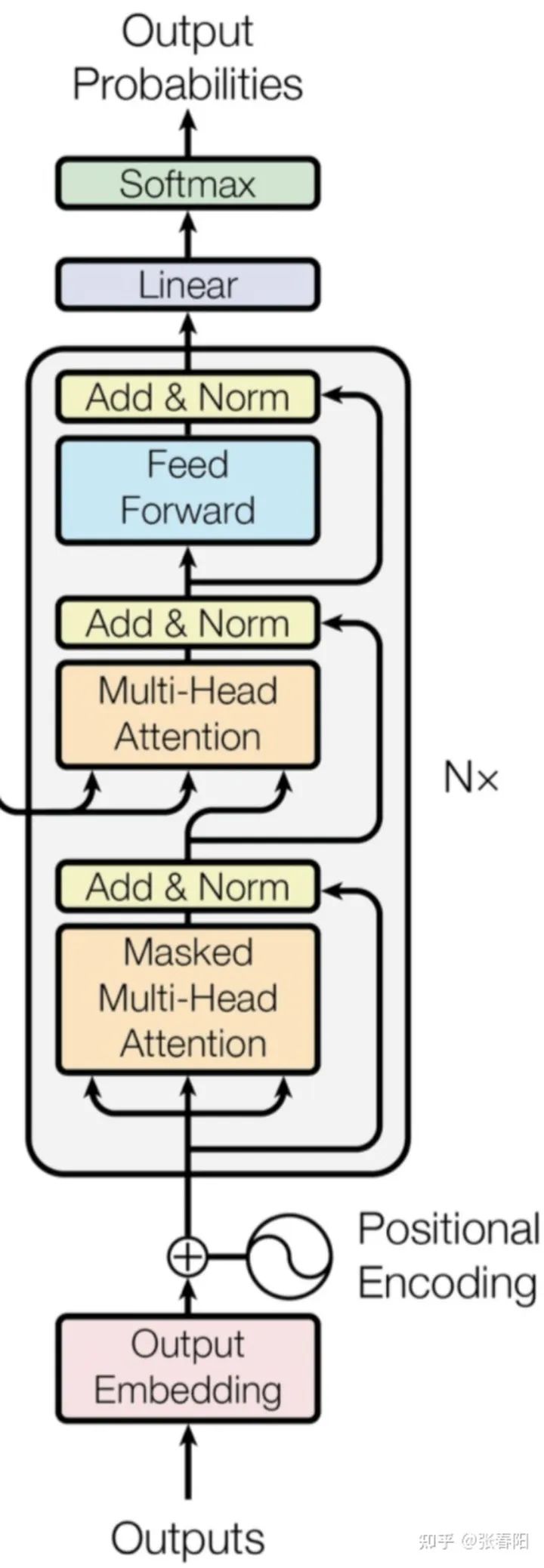
class DecoderLayer(nn.Module):
    def __init__(self, d_model, heads, dropout=0.1):        super().__init__()        self.norm_1 = Norm(d_model)        self.norm_2 = Norm(d_model)        self.norm_3 = Norm(d_model)                self.dropout_1 = nn.Dropout(dropout)        self.dropout_2 = nn.Dropout(dropout)        self.dropout_3 = nn.Dropout(dropout)                self.attn_1 = MultiHeadAttention(heads, d_model, dropout=dropout)        self.attn_2 = MultiHeadAttention(heads, d_model, dropout=dropout)        self.ff = FeedForward(d_model, dropout=dropout)
    def forward(self, x, e_outputs, src_mask, trg_mask):        x2 = self.norm_1(x)        x = x + self.dropout_1(self.attn_1(x2, x2, x2, trg_mask))        x2 = self.norm_2(x)        x = x + self.dropout_2(self.attn_2(x2, e_outputs, e_outputs, \        src_mask))        x2 = self.norm_3(x)        x = x + self.dropout_3(self.ff(x2))        return x

class Decoder(nn.Module):
    def __init__(self, vocab_size, d_model, N, heads, dropout):        super().__init__()        self.N = N        self.embed = Embedder(vocab_size, d_model)        self.pe = PositionalEncoder(d_model, dropout=dropout)        self.layers = get_clones(DecoderLayer(d_model, heads, dropout), N)        self.norm = Norm(d_model)
    def forward(self, trg, e_outputs, src_mask, trg_mask):        x = self.embed(trg)        x = self.pe(x)        for i in range(self.N):            x = self.layers[i](x, e_outputs, src_mask, trg_mask)        return self.norm(x)

7 Transformer

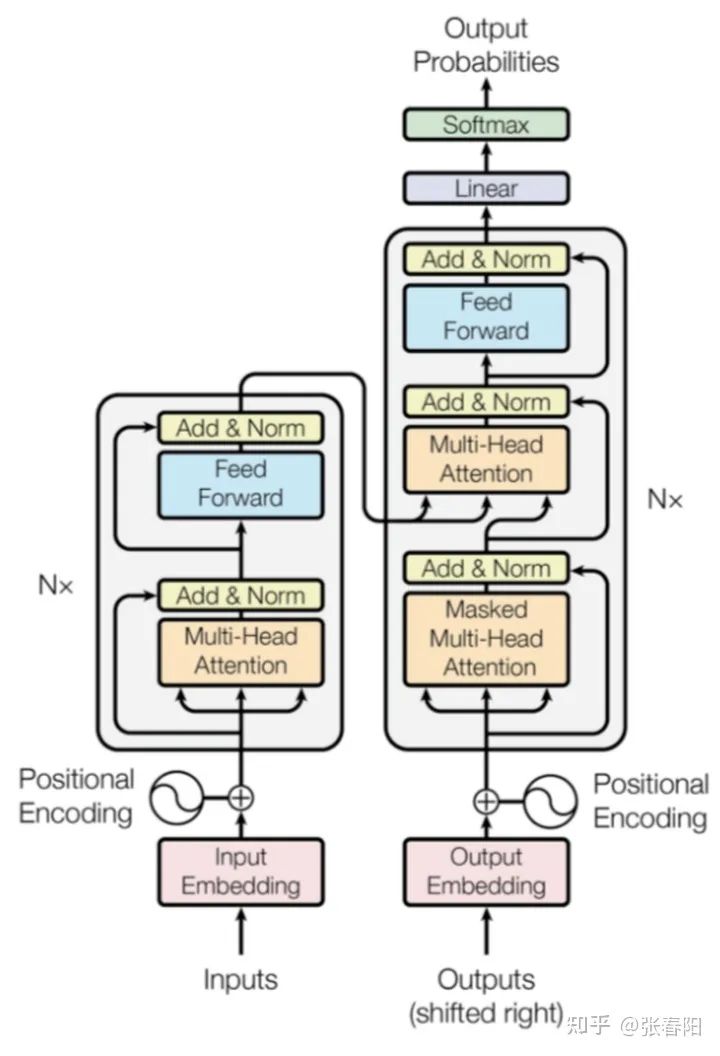
class Transformer(nn.Module):        def __init__(self, src_vocab, trg_vocab, d_model, N, heads, dropout):        super().__init__()        self.encoder = Encoder(src_vocab, d_model, N, heads, dropout)        self.decoder = Decoder(trg_vocab, d_model, N, heads, dropout)        self.out = nn.Linear(d_model, trg_vocab)            def forward(self, src, trg, src_mask, trg_mask):        e_outputs = self.encoder(src, src_mask)        d_output = self.decoder(trg, e_outputs, src_mask, trg_mask)        output = self.out(d_output)        return output

以上，就是 Transformer 实现的全过程，配套着 jupyter notebook 食用， 效果更加。

https://github.com/BSlience/transformer-all-in-onegithub.com

实现了上述这些，我们就得到了一个 Transformer 中的结构。

往期精彩：
【原创首发】机器学习公式推导与代码实现30讲.pdf
【原创首发】深度学习语义分割理论与实战指南.pdf
 谈中小企业算法岗面试
 算法工程师研发技能表
 真正想做算法的，不要害怕内卷
 技术学习不能眼高手低
 技术人要学会自我营销
 做人不能过拟合
点个在看