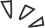Quanta Magazine:牛津大学数学家获得百年组合学问题进展

大数据文摘授权转载自zzllrr小乐
作者:Erica Klarreich
译者:zzllrr小乐
上图为一位数学家在梯子上将红色和蓝色珠子串在一个铺有蓝色圆圈的瓷砖红色背景上。
能把多少个红色和蓝色的珠子串在一起,而满足相同颜色不是平均间隔的?
使用压扁圆圈的半结构化模式,一位数学家打破了之前保持串珠长度的记录。
牛津大学的数学家Ben Green在理解一个有近 100 年历史的组合学问题方面取得了重大进展,表明最近的一个著名猜想“不仅错误,而且大错特错”,正如蒙特利尔大学的Andrew Granville所说。这篇新论文展示了如何创建比数学家想象的更长的无序彩色珠串,推广了 1940 年代已在计算机科学的许多领域找到应用的一系列工作。
这个猜想大约在 17 年前由过去半个世纪领先的离散数学家之一罗恩·格雷厄姆Ron Graham(也即葛立恒,由其中国台湾岳母起的中文名,小乐译注)提出,它关注的是你可以将多少个红色和蓝色珠子串在一起,而不会产生任何长的有单一颜色均匀间隔的序列。(你可以决定每种颜色的“长”分别有多长。)
这个问题是拉姆齐理论(Ramsey theory)中最古老的问题之一,它询问各种数学对象在必须出现有序之前可以增长到多大。串珠问题说起来容易,但看似困难:对于长串,串珠排列太多,无法一一尝试。
斯坦福大学的 Jacob Fox说:“有时这些看起来很基本的问题我们实际上几乎一无所知。” “我认为这是真正让很多人感到惊讶的问题之一,我们了解得多么少。”
近一个世纪以来,数学家们都知道,你不能无限地串珠子。一旦你为每种颜色选择了参数,你只能串起这么多珠子,然后被迫创建一个比你愿意容忍的更长的均匀间隔序列。随着红色和蓝色参数的增长,可以串珠的总数也会增长——但有多快呢?
在这个问题的一个版本中,即使是最短的均匀间隔的蓝色序列也被禁止,格雷厄姆推测存在一个简单的关系:最长可能的珠串的长度大致是红色珠子参数的平方。数学家积累的所有数值数据都支持格雷厄姆猜想。

2017年牛津大学的Ben Green
但现在Green证明了这个猜想是错误的。在一篇68 页的论文中,他展示了如何制造比 Graham 预测的更长的珠串。
“当 Ben 给我发一份草稿时,我很震惊,”新泽西州普林斯顿高等研究院的Sarah Peluse说。“我觉得这很神奇。”
Green的结构融合了几何学和动力系统来塑造无序的珠串,它建立在早期的珠串结构的基础上,该结构已在从矩阵乘法到密码学等学科中得到应用。Fox 说,这种结构“对于计算机科学中的问题非常重要”。
难以置信的模式
如果你对无序有强烈的兴趣,你可能会在你的字符串中禁止任何均匀间隔的序列。谈论只有两个珠子的均匀间隔序列是没有多少意义的,所以你(要做的是)尝试避免三个或更多珠子的序列。
你可以轻松串几颗珠子,但很快就会遇到困难。例如,如果你的前六个珠子是 RBBRBR,则无法继续。将蓝色珠子串起来,将均匀分布的珠子放在第 3、5 和 7 点;串一个红色的珠子将均匀间隔的珠子放在点 1、4 和 7。一个简单的计算机搜索表明,无论你如何开始你的珠子串,你都会被珠子 9 卡住。
如果要串八颗以上的珠子,就得给一点。也许你会决定你可以接受少于 5 个珠子的均匀间隔的蓝色序列和少于 12 个珠子的红色序列。1927 年,范德瓦尔登(Bartel Leendert van der Waerden) 证明,对于你选择的任何一对参数,你都会遇到一些有限的长度。这些长度现在称为范德瓦尔登数。(就像追随他的数学家一样,范德瓦尔登用着色数字而不是串珠来表达这个问题,但这两个公式是等价的。)

1985年德国波恩的范德瓦尔登(Bartel Leendert van der Waerden)
数学家很难准确地计算出范德瓦尔登数是如何随着参数的变化而变化的。但是如果你决定不容忍任何均匀间隔的蓝色序列——换句话说,如果你将蓝色参数固定为 3——那么似乎会出现一种模式。我们看到如果红色参数也是3,你会被9号珠子卡住。数学家计算过,如果红色参数为10,你会被97号珠子卡住;如果是15,你被218号珠子卡住;如果是 20 颗,则你被 389 号珠子卡住。在每种情况下,你可以串的珠子数量都非常接近红色参数的平方。到目前为止收集的所有数据都符合这种模式。
大约在 2004 年的某个时候,格雷厄姆推测该模式对于红色(red)参数的所有值(我们称之为r)继续存在。几年之内,数学家确实找到了制造长度接近r²的珠串的方法。但这还不足以证明猜想。它表明你可以串大约r² 个珠子而不会卡住,但它留下了你可以继续串更长珠子的可能性。
当格雷厄姆告诉Green这个猜想时,Green的直觉是它一定是错的。“这似乎根本不合理,”他说。
Green认为应该可以使用针对相关问题开发的结构来快速反驳这个猜想——在这个问题中,你试图避免均匀分布的蓝色序列,但你并不关心红色珠子的作用。对于这个问题,研究人员已经找到了在不产生蓝色序列的情况下装入许多蓝色珠子的方法。Green怀疑这些丰富的蓝色珠子会破坏任何潜在的红色长序列,即使珠串并不是专门为此目的而设计的。
但当他仔细观察这些珠串时,他发现蓝色珠子的分布方式留下了大片可以形成模式的红色区域。他意识到,这些例子不会导致范德瓦尔登问题的简单答案。
Green周期性地回到这个问题上,他花了一段时间试图证明格雷厄姆的猜想,因为他无法反驳它。他将其列入了 100 个未解决的数学问题清单,并写道:“我现在相信这个问题的答案可能是肯定的。”
即便如此,他说,“我认为我从未有过强烈的信念,认为这是真的。” 他说,重复这个猜想与其说是对他的信仰的陈述,不如说是“对他人的挑战”。
结构和随机性
Green并不满足于将问题留给其他数学家。当他坚信一个猜想是错误的但所有数据都表明它是正确的时,“我发现这是一个非常有吸引力的做尝试和努力的情况”他说。
他的直觉认为,应该存在比格雷厄姆预测的要长得多的无序珠串。如果早期的构造不能反驳这个猜想,他仍然觉得对它们进行一些修改可能会奏效。

已故的罗恩·格雷厄姆(葛立恒)是一位多才多艺的数学家和杂耍家
这些早期的珠串始于Felix Behrend 于 1946 年根据基本几何事实构建的结构。想象一张红纸上的蓝色圆圈。如果用一条线段连接圆上的两点,线段的中点在圆内,所以它是红色的。这三个点是均匀分布的,而且它们并不都是蓝色的。这是一个基本的观察,但通过将平面(或更高维度)上的点转换为珠子位置,Behrend 使用这种几何形状作为构造没有均匀间隔的蓝色序列的珠串的基础。
多年来,这种结构得到了广泛的应用。例如,去年年底,它形成了用于矩阵相乘的破纪录算法的关键成分之一。“Behrend 的构造出现在数量惊人的地方,”加州理工学院的David Conlon说。
为了解决范德瓦尔登问题,Green将注意力集中在以色列内盖夫的本古里安大学的Michael Elkin于 2008 年开发的Behrend工作的推广上,然后在当年晚些时候由Green本人和剑桥大学的Julia Wolf(朱莉娅·沃尔夫)进行了改进。在这次改进中,我们再次设想了一个红色背景上的蓝色圆圈(稍微加厚)。但是这一次,我们将这个设计想象成一个方形瓷砖,并使用相同的瓷砖副本来填充整个平面,在红色背景上创建一个重复的蓝色圆圈图案。
然后我们设想在平面上的某个点对珠串的起始端打上结,并在随机选择的方向上拉紧绳子,使其平放在平面上,不可预测地穿过红色和蓝色的地形。我们将珠子滑到绳子上,选择每个珠子的颜色以匹配珠子中心着陆点的颜色。Green 和 Wolf 表明,串在瓷砖上的动态路径通常会产生具有许多蓝色珠子但没有均匀间隔的蓝色序列的珠子串。
从范德瓦尔登问题的角度来看,这种结构的问题在于,为了防止形成蓝色序列,蓝色圆圈必须保持相当小。这会留下大片的红色,因此不可能在串起许多珠子的情况下而不创建出一个长的红色序列。
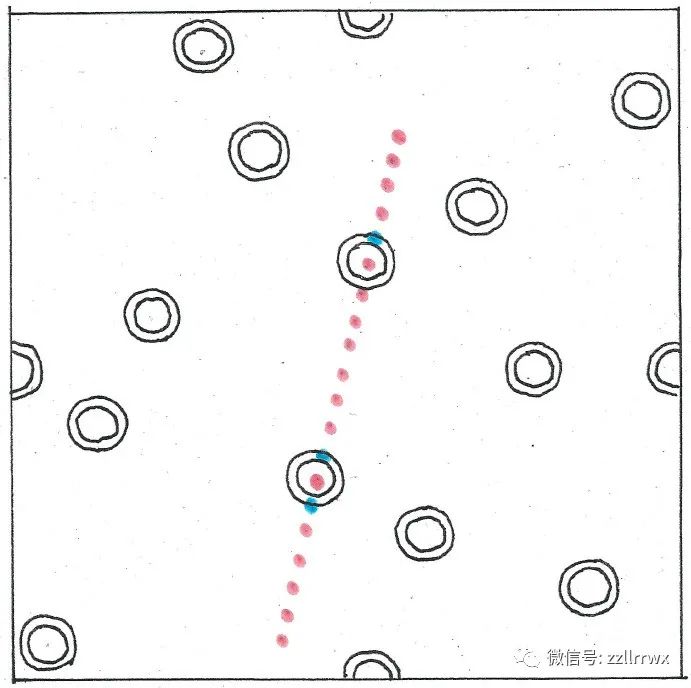
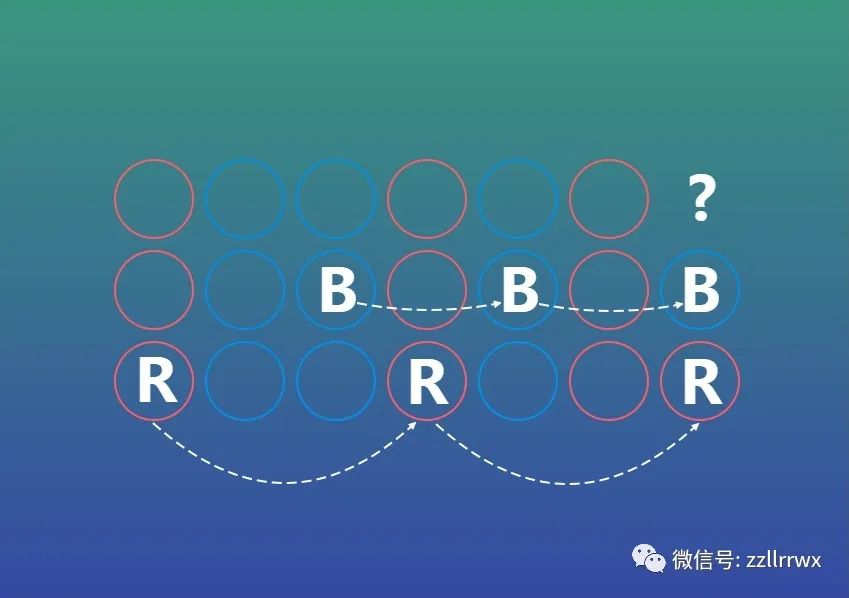
Green在会谈中使用的草图解释了他如何反驳格雷厄姆的猜想。
但在 2020 年的最后几天,在与妻子和孩子一起悠闲地散步时,Green突然有了一个见解:如果不是每块瓷砖一个蓝色的小圆圈,而是使用许多小圆圈,随意散落,会怎样?在接下来的一个月里,Green发现,如果你选择了正确大小和数量的圆圈并处理了一些额外的皱纹(例如,圆圈被稍微压扁),那么分散的蓝色圆圈将彻底破坏红色区域而不会造成形成蓝色序列的重要机会。这使得可以在不创建任何长的红色序列或任何蓝色序列的情况下串起许多珠子。
Green 能够证明,随着红色参数 ( r ) 的增加,最长的珠串长度最终会变得大于r²。然后,随着r继续增加,珠串最终将增长到大于r³ ——然后是r⁴、r⁵以及r的每一个更高的幂。换句话说,对于较大的r值,珠串比格雷厄姆预测的要长得多。
只有在r变得非常大之后,才会发生这些向r更高次方的跳跃。这可以解释为什么格雷厄姆一开始就被愚弄了:数学家收集的数据只经过了r的前几十个值,这些值太小而无法跳到更高的指数。
“这是一个非常棒的结果,”Conlon 说。当Green在二月份发表他的论文时,Conlon 给他发了一封电子邮件:“我已经很少对结果感到惊讶了,但这个让我感到惊讶。”
构造介于结构和随机性之间。有精心挑选的圆圈几何形状,以及各种随机选择:绳子的方向、珠子的大小、圆圈的挤压方式以及它们分散的位置。这是“结构化对象的随机结合,”Green说。“我认为这种直觉可能会出现在其他问题中。”
Peluse 说,拉姆齐理论中的大多数着色结构更倾向于随机性。“真的很难想出不是随机的颜色,”她说。“你必须有一个非常有见地的想法,就像Ben一样。”
Green的构造并不是范德瓦尔登问题的最终定论。就像早期的构造一样,他无法证明没有明显更长的珠串。上个月,牛津大学本科生扎克·亨特(Zach Hunter)已经设法通过修改Green的结构来向上推动珠串的长度,从而使圆的直径随机变化。但Fox 倾向于认为Green的结果可能与真正的范德瓦尔登数字相同。“我觉得这是一个非常令人满意的答案,”他说。
格雷厄姆2020年去世,享年 84 岁,比Green发表论文早了七个月。“罗恩(即罗恩·格雷厄姆,葛立恒)会非常兴奋,”Fox 说。
参考资料:
68页的论文
https://arxiv.org/abs/2102.01543
Graham的猜测
http://www.math.ucsd.edu/~fan/ron/papers/06_04_vdw.pdf
构造
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1078964/
Behrend的论文
https://arxiv.org/abs/0801.4310
Zach Hunter的论文
https://arxiv.org/abs/2111.01099
破纪录的矩阵乘法