求两个有序数组的中位数或者第k小元素
(给算法爱好者加星标,修炼编程内功)
作者:JustDoIT
https://www.cnblogs.com/TenosDoIt/p/3554479.html
问题:两个已经排好序的数组,找出两个数组合并后的中位数(如果两个数组的元素数目是偶数,返回上中位数)。
设两个数组分别是vec1和vec2,元素数目分别是n1、n2。
算法1:最简单的办法就是把两个数组合并、排序,然后返回中位数即可,由于两个数组原本是有序的,因此可以用归并排序中的merge步骤合并两个数组。
由于我们只需要返回中位数,因此并不需要真的合并两个数组,只需要模拟合并两个数组:每次选数组中较小的数,统计到第(n1+n2+1)/2个元素就是要找的中位数。算法复杂度为O(n1+n2)
int findMedian_merge(vector<int> &vec1, vector<int> &vec2){int N1 = vec1.size(), N2 = vec2.size();int medean = (N1 + N2 + 1) / 2, i = 0, j = 0;for(int k = 1; k < medean; k++){if(i < N1 && j < N2){if(vec1[i] < vec2[j])i++;else j++;}else if(i >= N1)//数组vec1到达末尾j++;else if(j >= N2)//数组vec2到达末尾i++;}if(i < N1 && j < N2)return vec1[i] < vec2[j] ? vec1[i] : vec2[j];else if(i >= N1)return vec2[j];else if(j >= N2)return vec1[i];}
讲下面的算法之前,先说2个结论
结论1:某个数组中有一半的元素不超过数组的中位数,有一半的元素不小于中位数(如果数组中元素个数是偶数,那么这里的一半并不是严格意义的1/2)。
结论2:如果我们去掉数组比中位数小的k个数,再去掉比中位数大的k个数,得到的子数组的中位数和原来的中位数相同。
算法2:利用折半查找的思想,假设两个数组的中位数分别是vec1[m1], vec2[m2]
1、如果vec1[m1] = vec2[m2] ,那么刚好有一半元素不超过vec1[m1],则vec1[m1]就是要找的中位数。
2、如果vec1[m1] < vec2[m2] 根据结论1很容易可以推理出,这个中位数只可能出现在vec1[n1/2,…,n1-1]或vec2[0,…,(n2-1)/2]中,那么vec1[n1/2,…,n1-1]和vec2[0,…,(n2-1)/2]的中位数是不是和原来两个数组的中位数相同呢?
根据结论2,如果原数组长度相等,即n1=n2,那么中位数不变;如果长度不相等,vec2中去掉的大于中位数的数的个数 > vec1中去掉的小于中位数的数的个数 ,则中位数不一定不变。因此我们要在两个数组中去掉相同个数的元素。
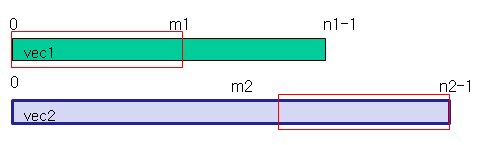
如下图所示,假设n1 < n2, 两个数组都去掉n1/2个元素,则子数组vec1[n1/2,…,n1-1]和vec2[0,…,n2-1-n1/2]的中位数和原来的中位数相同,图中红色方框里是去掉的元素。
注意:在n1
例如vec1 = [1,3,5,7],vec2 = [2,4,6,8], 如果我们要求的是上中位数,m1 = m2 =1,即3 < 4, 要删掉vec1的前半段,这里vec1[m1] = 3 要不要删除呢,我们只要判断一下3能否可能成为中位数,假设3是中位数,不超过3的数只有3个(1,2,3),总得元素有8个,因此3不可能成为上中位数,我们可以在vec1中删除2两个元素。
如果是求下中位数,即m1 = m2 = 2,即5 < 6,删除vec1前半段时要不要删除5呢?注意到比不超过5的数有5个,不低于5的数有4个,因此5有可能成为下中位数,因此5不能删除,vec1中只能删除左边两个元素。同理当vec1的个数是奇数时,vec1的中位数永远不能删除,即只能删除vec1的n1/2(整数除法)个元素
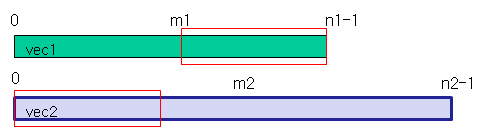
3、如果vec1[m1] > vec2[m2] ,同上分析,中位数只可能出现在vec1的前半段或vec2的后半段。如下图所示,两个数组分别去掉n1/2个元素后,子数组vec1[0,…,n1/2-1]和vec2[n1/2,…,n2-1]的中位数和原来的中位数相同
子数组递归求解,即可求出中位数,算法复杂度为O(log(n1+n2)).注意一下递归结束条件和边界处理。
int findMedian_logn(int vec1[], int n1, int vec2[], int n2){int m1 = (n1-1) / 2, m2 = (n2-1) / 2;if(n1 == 1){//递归结束条件if(n2 == 1)return vec1[0] < vec2[0] ? vec1[0] : vec2[0];if(n2 % 2 == 0){if(vec1[0] >= vec2[m2+1])return vec2[m2+1];else if(vec1[0] <= vec2[m2])return vec2[m2];else return vec1[0];}else{if(vec1[0] >= vec2[m2])return vec2[m2];else if(vec1[0] <= vec2[m2-1])return vec2[m2-1];else return vec1[0];}}else if(n2 == 1){//递归结束条件if(n1 % 2 == 0){if(vec2[0] >= vec1[m1+1])return vec1[m1+1];else if(vec2[0] <= vec1[m1])return vec1[m1];else return vec2[0];}else{if(vec2[0] >= vec1[m1])return vec1[m1];else if(vec2[0] <= vec1[m1-1])return vec1[m1-1];else return vec2[0];}}else{int cutLen = n1/2 > n2/2 ? n2/2 : n1/2;//注意每次减去短数组的一半,如果数组长度n是奇数,一半是指n-1/2if(vec1[m1] == vec2[m2])return vec1[m1];else if(vec1[m1] < vec2[m2])return findMedian_logn(&vec1[cutLen], n1-cutLen, vec2, n2-cutLen);elsereturn findMedian_logn(vec1, n1-cutLen, &vec2[cutLen], n2-cutLen);}}
算法3:这里我们把问题扩展一下,求两个有序数组的第k小的元素。
我们假设这个第k小的元素是X,若X在数组vec1的第i个位置,如果把X放到vec2中,那么X在排数组vec2中的第(k-i+1)个位置,则X >= vec2中第k-i个元素 且 X <= vec2中第k-i+1个元素。
因此我们可以首先假设元素X在数组vec1中,对vec1中的元素进二分查找。
选取vec1中的元素vec1[idx1](idx1 = n1/(n1+n2)*(k-1), 即第idx1+1个元素,由于不是中位数,因此不是选取中间元素),看vec2中的元素vec2[idx2](idx2 = k-idx1-2, 即第k-idx1-1个元素):
注意到这里的一个不变式:idx1及前面元素的个数 + idx2及前面元素的个数 = k,即(idx1+1)+(idx2+1)= k
如果vec1[idx1] == vec2[idx2] ,刚好有idx1+1+idx2+1 = k个元素不超过vec1[idx1], 则vec1[idx1]为所求
如果vec1[idx1] < vec2[idx2], 不超过vec1[idx1]的元素个数肯定小于k,因此vec1[idx1]以及其前面的元素肯定小于我们要求的元素;对于vec2[idx2+1]以及其后面的元素,不超过他们的数的个数肯定大于K个,因此vec2[idx2+1]以及其后面的元素肯定大于我们要求的元素。
故搜索范围缩小到vec1[idx1+1,…,n1-1] 和vec2[0...idx2]
如果vec1[idx1] > vec2[idx2], 同理搜索范围缩小到vec1[0...idx1]和vec2[idx2+1,....n2-1]
其实算法思想和上面的算法2相同。上述算法也可以每次取vec1和vec2的第k/2个元素比较,这样每次可以使k减小一半。
注意边界处理。算法中每次迭代平均k都会减小约k/2,因此算法复杂度为O(logk),而k = (n1+n2)/m, m是一个常数,即复杂度为O(log(n1+n2))
//找到两个有序数组中第k小的数,k>=1int findKthSmallest(int vec1[], int n1, int vec2[], int n2, int k){//边界条件处理if(n1 == 0)return vec2[k-1];else if(n2 == 0)return vec1[k-1];if(k == 1)return vec1[0] < vec2[0] ? vec1[0] : vec2[0];int idx1 = n1*1.0 / (n1 + n2) * (k - 1);int idx2 = k - idx1 - 2;if(vec1[idx1] == vec2[idx2])return vec1[idx1];else if(vec1[idx1] < vec2[idx2])return findKthSmallest(&vec1[idx1+1], n1-idx1-1, vec2, idx2+1, k-idx1-1);elsereturn findKthSmallest(vec1, idx1+1, &vec2[idx2+1], n2-idx2-1, k-idx2-1);}
算法4:对于寻找两个有序数组第k小的元素,还有一种简化算法1,复杂度为O(k)的算法,在归并两个数组的过程中,如果如果已经选择的元素达到k,就不需要再归并下去了。
推荐阅读:
专注服务器后台技术栈知识总结分享
欢迎关注交流共同进步
