同济版《线性代数》再遭口诛笔伐，网友：它真的不太行-技术圈

明敏发自凹非寺

量子位报道 | 公众号 QbitAI

最近，又有网友在知乎开帖，将自己总结的 线性代数逻辑框架 分享了出来，本来仅仅只是学习分享，没想到又又又把 同济版线性代数 拉出来鞭尸一回。

开帖如下：

对于楼主的框架，广大网友表示不应该把矩阵作为理解线性代数的核心。

答主@杨数森表示，线性代数的最核心问题就是怎样的线性变换是相似的。

最好不要把矩阵作为线性代数的核心，就像不要把初等函数作为微积分的核心一样。

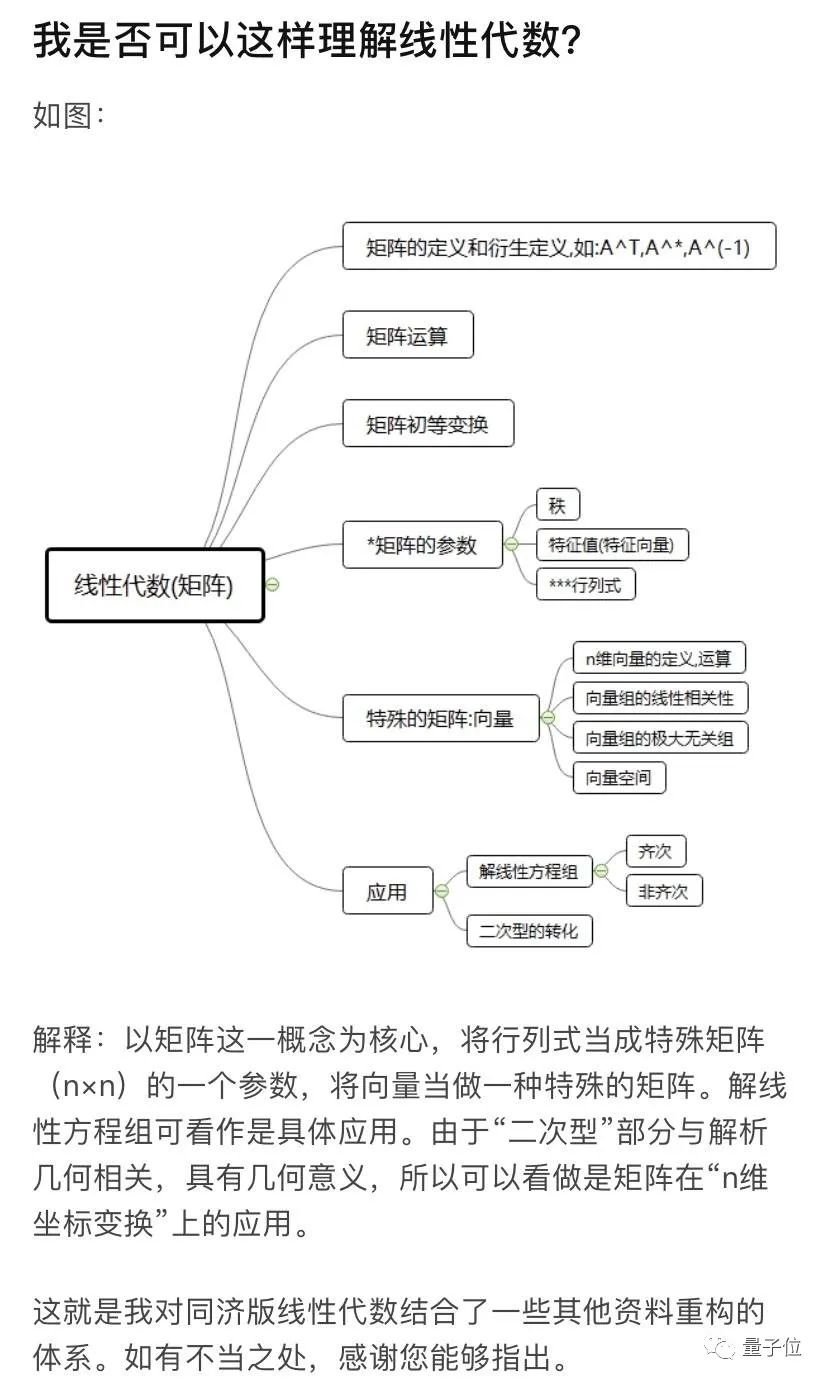
线性代数的最核心问题就是怎样的线性变换是相似的，而这些相似的线性变换具有怎样的特征。引入特征值为这个问题提供了巨大的帮助，却不够彻底，因为尚不能解释为何存在非零的幂零变换。
经过复杂的讨论，我们知道复线性变换的 Jordan 标准型是判断线性变换是否相似的标志，也是衡量线性变换的特征的方式。
所谓两个线性变换是相似的，就是它们能在适当的基下表示成相同的矩阵，而 Jordan 标准型就是其中的代表。
为了把线性代数应用到分析和几何领域，需要在线性空间中引入度量，而内积正是确定度量的巧妙方法。
欧氏空间是带有内积的线性空间，其中的内积是正定、对称的双线性函数。在有限维欧氏空间中，能够顺应所给内积的基是标准正交基，保持内积不变的变换是正交变换。欧氏空间中的另一个有意义的变换是对称变换，而它也恰好对应于二次型。

也有网友认为，向量空间、线性空间以及线性空间之间的态射应该是线性代数的核心。

更有网友表示，之所以会产生这样的误解，很大原因是教材的编写框架对人造成了误导。

同济版《线性代数》再一次被推到了风口浪尖。

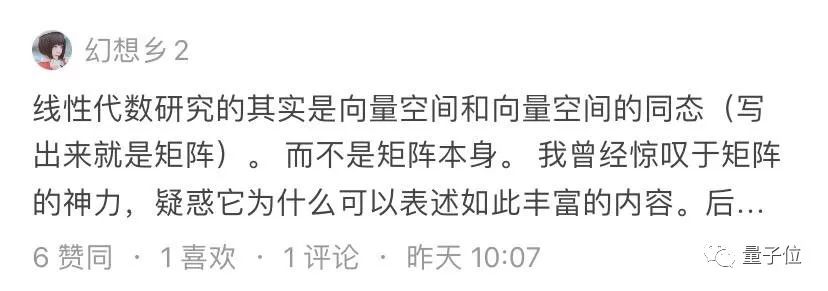
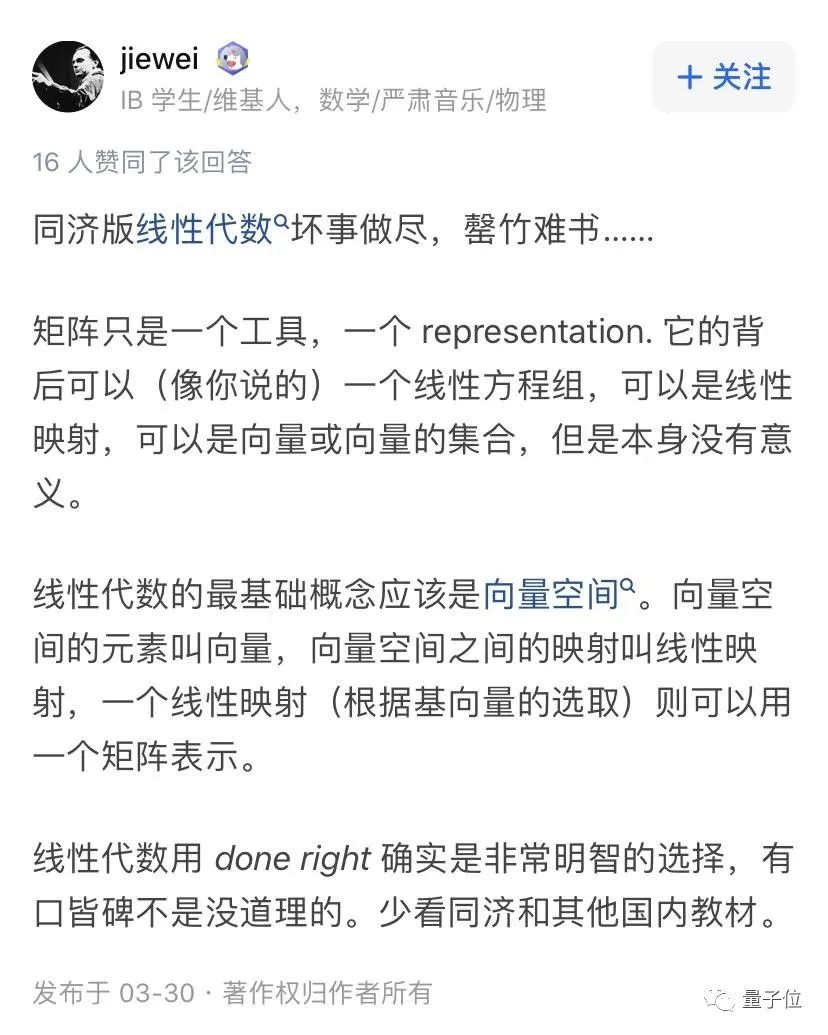
同济版《线性代数》为何会引起众怒？

同济版《线性代数》为何会频频引起“众怒”呢？

早在2019年，知乎上便有了关于这版教材的吐槽讨论：同济版《线性代数》引发激烈争议！

吐槽理由主要在于教材章节混杂、原理晦涩难懂，往往学完一本书也不明所以。

最令人诟病的便是教材内容编排不合理，无论是从行列式开始、还是从矩阵入手，教材开篇生硬地引入大量全新的概念，对于广大学子而言都深感莫名其妙。

尽管学习了行列式，但是大家行列式的认识也只停留在盲目做习题这一层面，把这行乘一个系数加到另一行上，再把另一行减过来，但是却不明白这么来回折腾的意义是什么。

此外，作为一门本身就十分抽象的学科，同济版《线性代数》对于许多概念的解释仍旧是冗长的下定义模式，缺乏直观的几何理解，这也使许多人更加不理解学习线性代数的意义。

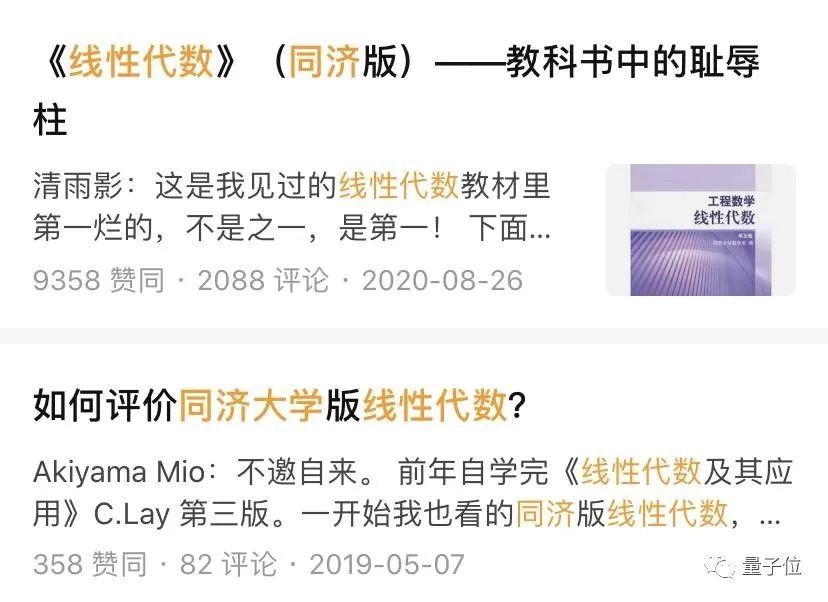
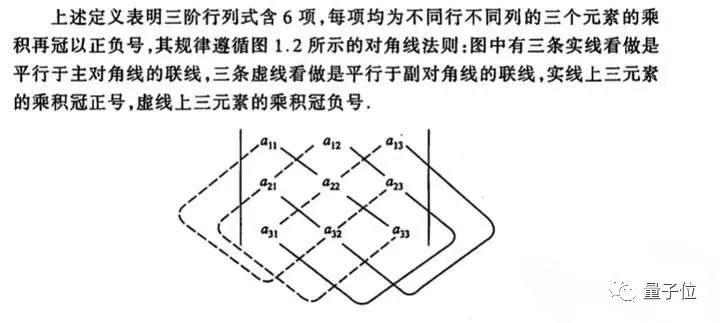
△定义虽然讲解了对角线法则，但是却没有解释为什么四阶行列式开始便不使用该方法

不够合理的课程内容编排、晦涩难懂的定义原理，让人感觉这不是在学习一门课程，而是被不由分说地抛到一个强制的世界中，只是在考试的皮鞭下被迫赶路。

你的线性代数，之前可能都学错了

其实，同济版《线性代数》之所以会饱受吐槽，还有一个更大的原因：无论是科研还是实际工程应用，线性代数的身影无处不在。如果没有理解其中原理，在日后的运用中可谓是步履维艰。

CSDN 副总裁孟岩曾在《理解矩阵》一文中表示“不少人即使能够很熟练地以线性代数为工具进行过科研和应用工作，但是对于很多初学者提出来的看上去很基础的问题并不清楚。”

比如说：矩阵究竟是什么东西？向量可以被认为是具有n个相互独立性质（维度）的对象的表示，矩阵又是什么呢？
如果认为矩阵是一组列（行）向量组成的新的复合向量的展开式，那么为什么这种展开式具有如此广泛的应用？
特别是为什么偏偏二维的展开式如此有用？如果矩阵中每一个元素又是一个向量，那么再展开一次，变成三维的立方阵，是不是更有用？

面对这一类的问题，许多老手们就好像大人在面对小孩子的刨根问底，最后总会迫不得已地说：“就是这么规定的，你接受并且记住就好。”

然而这样的问题如果不能获得回答，线性代数对于学习者而言就是一个简单粗暴的、莫名其妙的规则合集。

这种过分强调形式论证、忽略直觉思维的教学形式，也会在一定程度上限制学习者的创新能力，使最后培养出来的学生也只能熟练地应用工具，缺乏真正意义上的理解。

正确学习姿势

对此，不少“过来人”为初学者推荐了这些课程，可以帮助大家更好学习理解线性代数：

1. Gilbert Strang的「线性代数 MIT 18.06」课程及教材《Introduction to Linear Algebra》

不同于国内教材，Strang的课程更加面向实际应用、难度适中，比较注重从实际问题中培养数学直觉，适合工程学科学生使用。

并且在课程中，Strang会先引入有趣的数学事实，然后讨论为什么这样是对的，再留一些习题让学习者自己去深入探究原理，培养学习者对线性代数的兴趣。课程链接：86岁还在录网课：MIT教授Gilbert Strang最新「线性代数」课程上线，被清华选作教材

另外，这个神课东哥发现网易公开课上也有视频教程，感兴趣可以配合教材一起学习。

链接：https://open.163.com/newview/movie/courseintronewurl=%2Fspecial%2Fopencourse%2Fdaishu.html

2. J. Ström, K. Åström 和 T. Akenine-Möller的《沉浸式线性代数》教程（《Immersive Linear Algebra》）

教程链接：http://immersivemath.com/ila/index.html

这份教程不再是简单、枯燥的文字+公式组成，而是包含了大量生动有趣的动画演示，用交互的方式进行学习。

在阅读内容的时候，学习者可以自己去移动其中的动图，变换参数，从不同的角度来理解其中的知识。

3. 蓝以中的《高等代数简明教程》和丘维声的《简明线性代数》

如果有的同学对英文比较头大，也可选择国内这两位老师的课程学习。

关于线性代数教材，你有想分享或吐槽的内容吗？

参考链接：
知乎话题：https://www.zhihu.com/question/448135596
“杨数森”的回答（已获授权）：https://www.zhihu.com/question/448135596/answer/1805794712
《理解矩阵》：https://wenku.baidu.com/view/f96956b404a1b0717fd5ddca.html

················· END ·················

长按进入小程序，进行打卡签到
新一期打卡签到，奖品超多

（更多精彩值得期待……）
最近热文：
一周内被程序员疯转5.6W次，最终被大厂封杀！
字节跳动《算法中文手册》火了，完整版 PDF 开放下载！
改个圆角200万？原研哉是怎么“说服”小米的？
2个敏感资源，密码666 ᥬ🤩 ᭄
支付宝加密规则，你真的懂吗？
LeetCode1-220题汇总，希望对你有点帮助！

2T技术资源大放送！包括但不限于：C/C++，Linux，Python，Java，人工智能，考研，软考，英语，等等。在公众号内回复「资源」，即可免费获取！回复「社群」，可以邀请你加入读者群！


❤️给个「在看」，是对我最大的支持❤️

同济版《线性代数》再遭口诛笔伐，网友：它真的不太行

明敏 发自 凹非寺

量子位 报道 | 公众号 QbitAI