【文末有福利】股票跨度——真实世界的算法
日期:2020年08月15日
正文共:12997字10图
预计阅读时间:33分钟
来源:《真实世界的算法:初学者指南》


1.1算法

1.2运行时间和复杂度
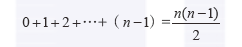

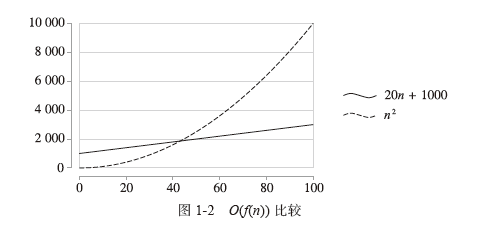
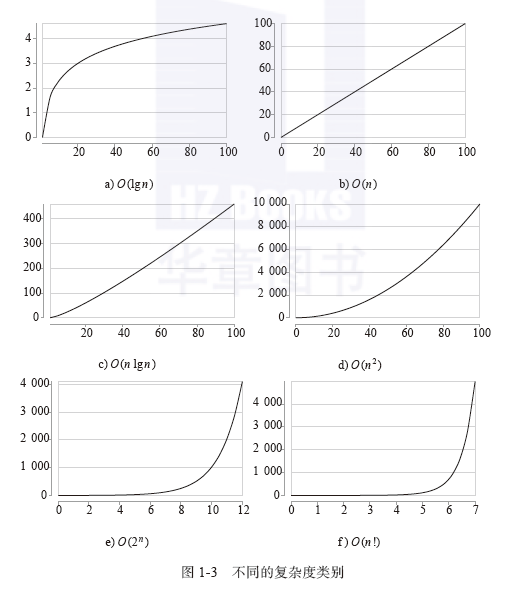
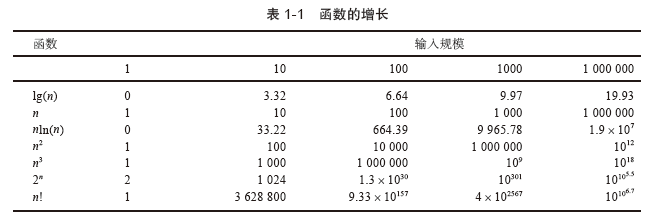
1.3使用栈求解股票跨度
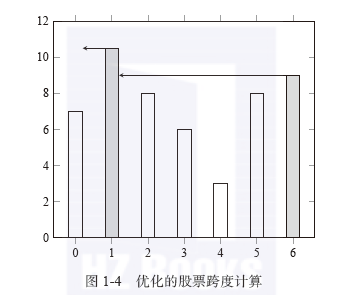
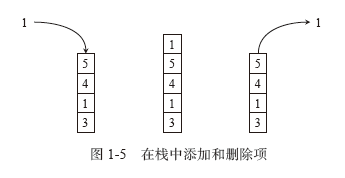

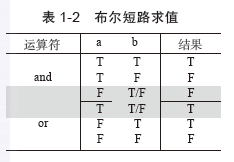
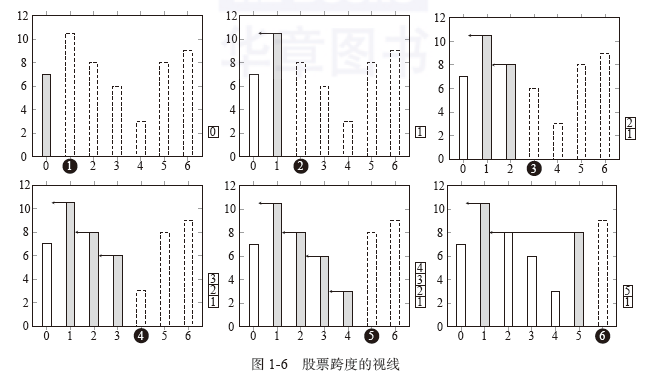


粉丝福利时间
评论区留言,点赞数前5可获得此书!!!
以48个小时计!
注:若是在活动截止日期后24小时内无法取得用户回复或联系,将按照留言点赞排名顺延。
— THE END —

评论
 下载APP
下载APP日期:2020年08月15日
正文共:12997字10图
预计阅读时间:33分钟
来源:《真实世界的算法:初学者指南》


1.1算法

1.2运行时间和复杂度




1.3使用栈求解股票跨度







粉丝福利时间
评论区留言,点赞数前5可获得此书!!!
以48个小时计!
注:若是在活动截止日期后24小时内无法取得用户回复或联系,将按照留言点赞排名顺延。
— THE END —
