笔记|李宏毅老师机器学习课程,视频4回归示例
《学习笔记》专栏·第4篇
文 | MLer
1965字 | 6分钟阅读
【数据科学与人工智能】开通了机器学习群,大家可以相互学习和交流。请扫描下方二维码,备注:姓名-ML,添加我为好友,诚邀你入群,一起进步。
感谢李宏毅老师的分享,他的课程帮助我更好地学习、理解和应用机器学习。李老师的网站:http://speech.ee.ntu.edu.tw/~tlkagk/index.html。这个学习笔记是根据李老师2017年秋季机器学习课程的视频和讲义做的记录和总结。因为这个视频是在Youtube上面,有些朋友可能无法观看,我把它搬运下来放在云盘上面,大家点击阅读原文,就可以直接在手机随时随地观看了。再次,感谢李老师的付出和贡献。
这门课,共有36个视频,每个视频播放的时间不一。我按着视频播放的顺序,观看,聆听和学习,并结合讲义,做学习笔记。我做学习笔记目的有三:
1 帮助自己学习和理解机器学习
2 记录机器学习的重要知识、方法、原理和思想
3 为传播机器学习做点事情
视频4:回归示例
一、梯度下降法寻找best function
一个简单的一元线性回归为例,演示梯度下降算法寻找best function的过程。
程式采用Python3和Jupyter notebook 来示范。你若是要运行这些代码,请先构建好Python和数据科学的工作环境,推荐安装Anaconda软件。
代码如下:
1 导入所需Python库
import numpy as npimport matplotlib.pyplot as plt%matplotlib inline
2 模拟数据设计和生成
x_data = [338., 333., 328., 207., 226., 25., 179., 60., 208., 606.]y_data = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]# ydata = b + w * xdata
3 穷举b和w在一定范围里面所对应的Loss的值
x = np.arange(-200, -100, 1) # biasy = np.arange(-5, 5, 0.1) # weightZ = np.zeros((len(x), len(y)))for i in range(len(x)):for j in range(len(y)):b = x[i]w = y[j]Z[j][i] = 0for n in range(len(x_data)):Z[j][i] = Z[j][i] + (y_data[n] - b - w * x_data[n]) ** 2Z[j][i] = Z[j][i]/len(x_data)
4 利用梯度下降算法寻找Best function所对应的最佳的参数w和b
# 利用梯度下降算法# ydata = b + w * xdatab = -120 # initial bw = -4 # initial wlr = 0.0000001 # learning rateiteration = 100000 # 迭代次数# 记录初始值,用于可视化b_history = [b]w_history = [w]# Iterationsfor i in range(iteration):b_grad = 0.0w_grad = 0.0for n in range(len(x_data)):b_grad = b_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * 1.0w_grad = w_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * x_data[n]# update parametersb = b - lr * b_gradw = w - lr * w_grad# 记录用来画图的参数值b_history.append(b)w_history.append(w)# 绘制可视化plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet'))plt.plot([-188.4], [2.67], 'x', ms=12, markeredgewidth=3, color='orange')plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')plt.xlim(-200, -100)plt.ylim(-5, 5)plt.xlabel(r'$b$', fontsize=16)plt.ylabel(r'$w$', fontsize=16)plt.show()
结果1:
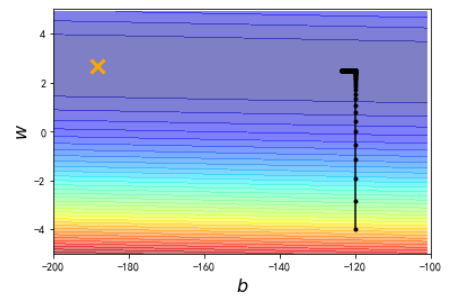
横纵表示bias的取值,纵轴表示weight的取值,不同颜色用于区分在(b,w)下的Loss值差异,颜色越深,表示Loss值越大。黄色的叉表示最佳的(b,w)。我们当前的学习速率,经过10万次迭代后,没有找到最佳的(b,w),修改学习速率的值,放大10倍后,见结果2:
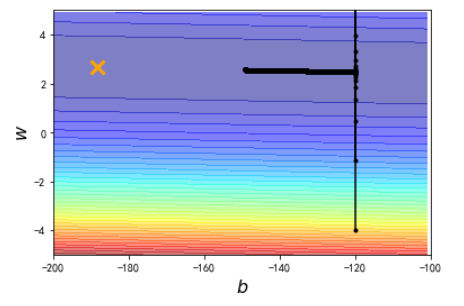
我们发现离黄色的叉还是有一定距离,我们继续把学习速率放大10倍,见结果3:
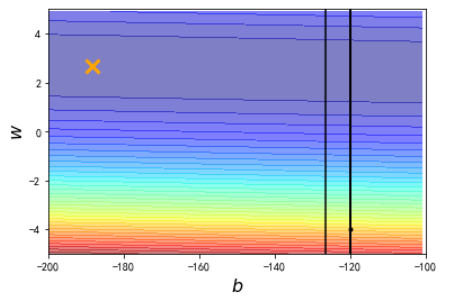
此时,已经无法收敛到黄色的叉位置。我们如何解决这个问题?这个时候要采用梯度下降算法的变体,对b和w采用不同的学习速率来更新参数的值,代码如下:
# 利用梯度下降算法# 给b,w 特质化的学习率# ydata = b + w * xdatab = -120 # initial bw = -4 # initial wlr = 1 # learning rateiteration = 100000 # 迭代次数# 记录初始值,用于可视化b_history = [b]w_history = [w]lr_b = 0lr_w = 0# Iterationsfor i in range(iteration):b_grad = 0.0w_grad = 0.0for n in range(len(x_data)):b_grad = b_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * 1.0w_grad = w_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * x_data[n]lr_b = lr_b + b_grad ** 2lr_w = lr_w + w_grad ** 2# update parametersb = b - lr/np.sqrt(lr_b) * b_gradw = w - lr/np.sqrt(lr_w) * w_grad# 记录用来画图的参数值b_history.append(b)w_history.append(w)# 绘制可视化plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet'))plt.plot([-188.4], [2.67], 'x', ms=12, markeredgewidth=3, color='orange')plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')plt.xlim(-200, -100)plt.ylim(-5, 5)plt.xlabel(r'$b$', fontsize=16)plt.ylabel(r'$w$', fontsize=16)plt.show()
结果4:
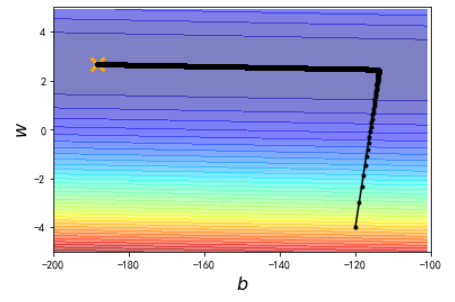
这时候,可以收敛到最佳的(b,w)位置了。
思考题:
1 梯度下降算法的权重更新,学习速率的设置会带来什么影响?
2 学习速率有哪些控制方法?
代码链接:
https://github.com/wangluqing/MachineLearning/blob/master/ML_Course/regression_demo.ipynb
朋友们,在学习中有什么问题或者想法,请加入机器学习群,大家一起讨论,共同进步。
每周一书
课程视频点击
↓↓↓
