LeetCode刷题实战300：最长递增子序列-技术圈

算法的重要性，我就不多说了吧，想去大厂，就必须要经过基础知识和业务逻辑面试+算法面试。所以，为了提高大家的算法能力，这个公众号后续每天带大家做一道算法题，题目就从LeetCode上面选！

今天和大家聊的问题叫做 最长递增子序列，我们先来看题面：

https://leetcode-cn.com/problems/longest-increasing-subsequence/

Given an integer array nums, return the length of the longest strictly increasing subsequence.

A subsequence is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例

示例 1：

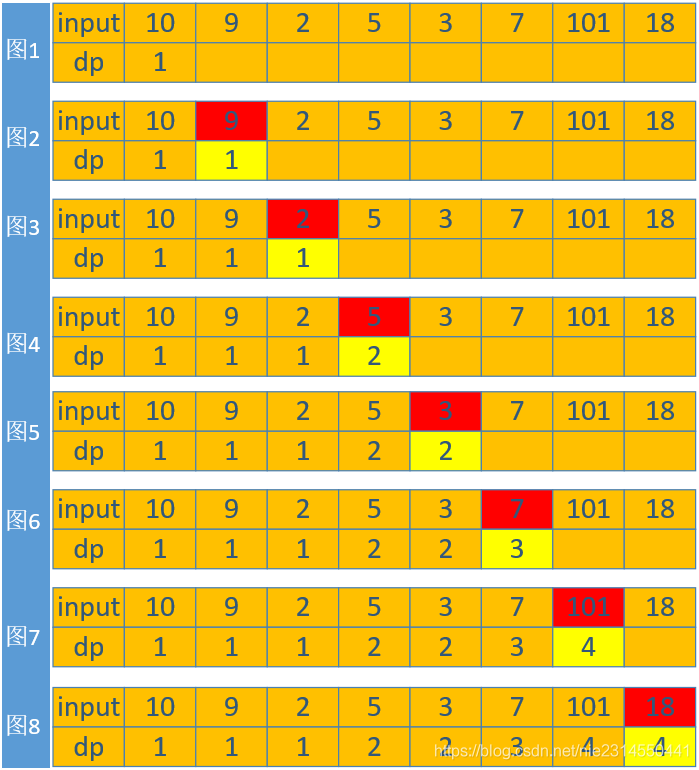
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

解题

https://blog.csdn.net/nie2314550441/article/details/107269090

3.1 方法一：动态规划

动态规划递推公式：dp[i]=max(dp[j])+1,其中0≤j<i且num[j]<num[i]。

复杂度分析：

时间复杂度：O(n^2)

空间复杂度：O(n)

以输入序列 [10,9,2,5,3,7,101,18]为例，数组变化如下图所示

3.2 方法二：贪心 + 二分查找

贪心法 + 二分法：使用数组来进行上升序列的积累。如果上升则积累（append），如果下降，则通过二分法找到探索元素的位置进行替换（不改变数组的长度）。最终返回数组的长度。

设当前已求出的最长上升子序列的长度为 len（初始时为 1），从前往后遍历数组 nums，在遍历到 nums[i] 时：

如果 nums[i]>dp[len] ，则直接加入到 dp 数组末尾，并更新 len=len+1；

否则，在 d 数组中二分查找，在 dp 数组中找到第一个大于或等于 nums[i] 的数 dp[k] ，并更新 d[k]=nums[i]。

复杂度分析：

时间复杂度：O(nlogn)

空间复杂度：O(n)

以输入序列 [10,9,2,5,3,7,101,18]为例，数组变化如下图所示：

最终得到最大递增子序列长度为 4。

#pragma once
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
 
#define NAMESPACE_LENGTHOFLIS namespace NAME_LENGTHOFLIS {
#define NAMESPACE_LENGTHOFLISEND }
NAMESPACE_LENGTHOFLIS
 
// 动态规划
// 递推公式：dp[i]=max(dp[j])+1,其中0≤j<i且num[j]<num[i]
// 时间复杂度：O(n^2), 空间复杂度：O(n)
class Solution1 
{
public:
    int lengthOfLIS(vector<int>& nums) 
    {
        int n=(int)nums.size();
        if (n == 0) return 0;
        vector<int> dp(n, 0);
        int maxLen = 1;
        for (int i = 0; i < n; ++i) 
        {
            dp[i] = 1;
            for (int j = 0; j < i; ++j) 
            {
                if (nums[j] < nums[i])
                {
                    dp[i] = max(dp[i], dp[j] + 1);
                    maxLen = max(maxLen, dp[i]);
                }
            }
        }
        
        //return *max_element(dp.begin(), dp.end());
        return maxLen;
    }
};
 
// 动态规划
// dp[i] = max(dp[j]) + 1, 其中 0 ≤ j < i 且 num[j] < num[i] 
class Solution
{
public:
  // 返回不小于目标值的位置 
    int search(vector<int> & nums, int target)
    {
        int l = 0;
        int r = nums.size() - 1;
        while(l < r)
        {
            int mid = (r + l) / 2;
            if(target == nums[mid])
               return mid;
            else if(target > nums[mid])
               l = mid + 1;
            else if(target < nums[mid])
               r = mid;
        }
        return l;
    }
 
    int lengthOfLIS(vector<int>& nums) 
    {
        int len = nums.size();
        vector<int> dp;
        if(len <= 0) return 0;
        dp.push_back(nums[0]);
        for(int i = 1;i < len;i++)
        {
            if(nums[i] > dp[dp.size() - 1])
                dp.push_back(nums[i]);
            else
            {
                 //auto it = lower_bound(dp.begin(), dp.end(), nums[i]);
                //*it = nums[i];
 
                int p = search(dp,nums[i]);
                dp[p] = nums[i];
            }
        }
 
         return dp.size();
    }
};
 
以下为测试代码//
// 测试 用例 START
void test(const char* testName, vector<int>& nums, int expect)
{
    Solution_1 s1;
    int result1 = s1.lengthOfLIS(nums);
    Solution_2 s2;
    int result2 = s2.lengthOfLIS(nums);
    if (expect == result1 && expect == result2)
        cout << testName << ", solution passed." << endl;
    else
        cout << testName << ", solution failed. expect:" << expect << ", result1:" <<result1 << ", result2:" << result2 << endl;
}
 
// 测试用例
void Test1()
{
    vector<int> nums = { 10,9,2,5,3,7,101,18 };
    int expect = 4;
    
    test("Test1()", nums, expect);
}
 
void Test2()
{
    vector<int> nums = { 10,11,1,2,3,12,13,4 };
    int expect = 5;
 
    test("Test2()", nums, expect);
}
 
NAMESPACE_LENGTHOFLISEND
// 测试 用例 END
//
 
void LengthOfLIS_Test()
{
    NAME_LENGTHOFLIS::Test1();
    NAME_LENGTHOFLIS::Test2();
}