本篇推文共计2000个字，阅读时间约3分钟。

题目描述：

给一个整数数组nums，

找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。

例如举例所示：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是[2,3,7,101]，因此长度为4。

输入：nums = [0,1,0,3,2,3]
解释：最长递增子序列是[0,1,2,3]，因此长度为4。

由题目描述可知

设数组dp[i]的值代表数组nums

前i个数字的最长递增子序列长度

设j∈[0,i)，每轮计算新dp[i]时，

遍历[0,i)列表区间，做以下判断：

1.当nums[i]>nums[j]时：

nums[i]可以接在nums[j]之后（此题要求严格递增），
此情况下最长上升子序列长度为
dp[i]=dp[j]+1；

2.当nums[i]<=nums[j]时：

nums[i]无法接在nums[j]之后，
此情况上升子序列不成立，跳过

在情况1中，计算出dp[j]+1的最大值，即为数组nums的最长上升子序列长度。

具体实现的办法可以使用遍历j时，每轮执行最大值比较公式：

dp[i]=max(dp[i],dp[j]+1)

将遍历每一轮的最长上升子序列长度存入数组dp[i]中

在初始化时

将dp[i]所有元素置为1，含义为每个元素都至少可以单独成为子序列，此时长度为1

例如此种情况：

nums=[2,2,2,2,2]
则该数组nums的最长上升子序列为1

我们用一个实际的例子，来解答此题

首先判断数组nums非空，如果是一个空数组

则not nums=1

if 1 则返回 0(即不会执行后面代码操作)

if not nums:
    return 0

接下来我们用一个非空数组nums解释下面的代码

设置nums=[10,12,11,9,15,13,21]

设置dp=[1,1,1,1,1,1,1]

dp=[1]*len(nums)

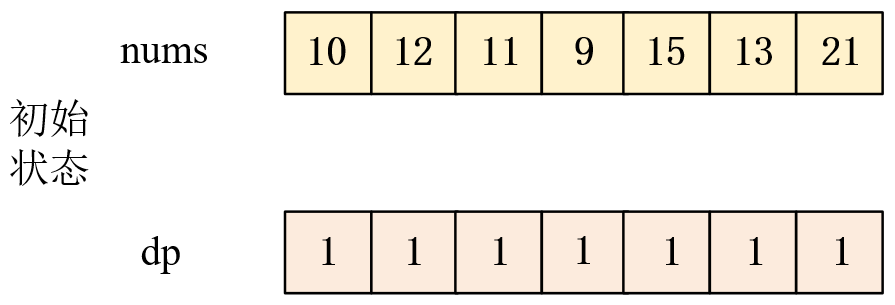
如下图所示即为初始状态数组nums与dp的值

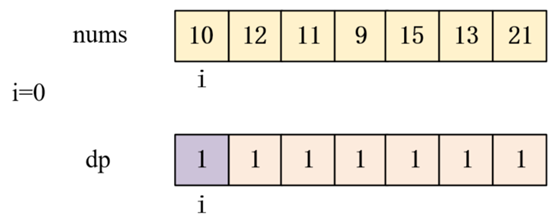
当i=0时，此时数组nums[10,12,11,9,15,13,21]中

只有[10]一个子数列，

所以此时最长上升子序列为[10]

最长上升子序列长度dp=1,如下图紫色区域标出。

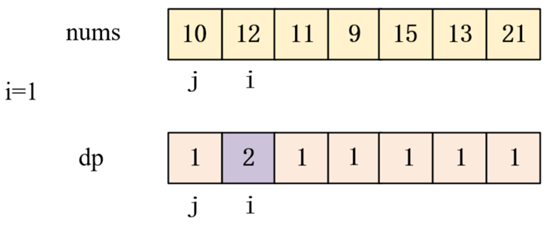
当i=1时，此时数组nums[10,12,11,9,15,13,21]中

只有[10,12]一个子数列，

所以此时最长上升子序列为[10,12]

最长上升子序列长度dp=2,如下图紫色区域标出。

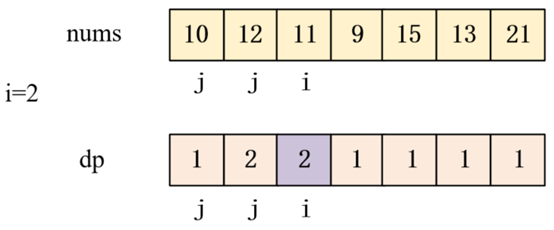
当i=2时，此时数组nums[10,12,11,9,15,13,21]中

此时数列为[10,12,11]，

此时最长上升子序列为[10,12]

最长上升子序列长度dp=2,如下图紫色区域标出。

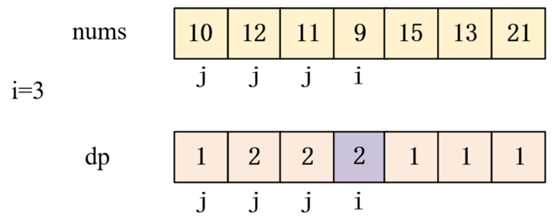
当i=3时，此时数组nums[10,12,11,9,15,13,21]中

此时数列为[10,12,11,9]，

此时最长上升子序列为[10,12]

最长上升子序列长度dp=2,如下图紫色区域标出。

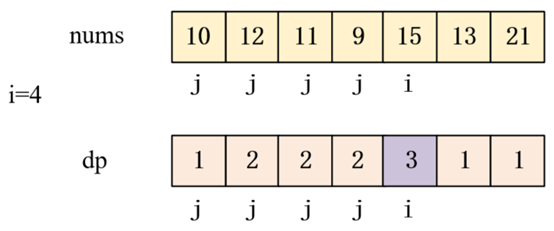
当i=4时，此时数组nums[10,12,11,9,15,13,21]中

此时数列为[10,12,11,9,15]，

此时最长上升子序列为[10,12,15]

最长上升子序列长度dp=3,如下图紫色区域标出。

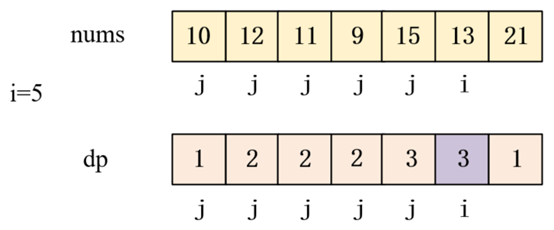
当i=5时，此时数组nums[10,12,11,9,15,13,21]中

此时数列为[10,12,11,9,15,13]，

此时最长上升子序列为[10,12,15]

最长上升子序列长度dp=3,如下图紫色区域标出。

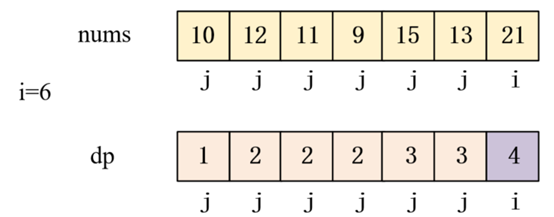
当i=6时，此时数组nums[10,12,11,9,15,13,21]中

此时数列为[10,12,11,9,15,13,21]，

此时最长上升子序列为[10,12,15,21]

最长上升子序列长度dp=4,如上图紫色区域标出。

最后返回记录i从0到6的数组dp[i]最大值即可

return max(dp)

完整代码如下：

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        dp=[1]*len(nums)
        for i in range(len(nums)):
            for j in range(i):
                if nums[j]<nums[i]:
                    dp[i]=max(dp[i],dp[j]+1)
        return max(dp)