线性映射: 从凯莱引入矩阵乘法说起
1引言
在现代数学中,线性映射(也称为线性变换或在某些情况下称为线性函数)是两个模(例如,两个向量空间)之间的映射
线性映射始终将线性子空间映射到线性子空间,不过注意,可能会映射到较低维的子空间;例如,它可以将过原点的平面映射到平面、直线或者点。
线性映射通常可以表示为矩阵,简单例子包括旋转和反射线性变换。
例子
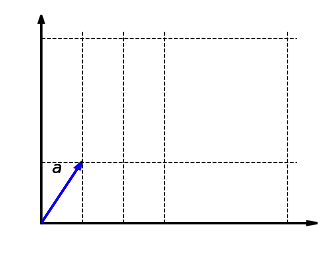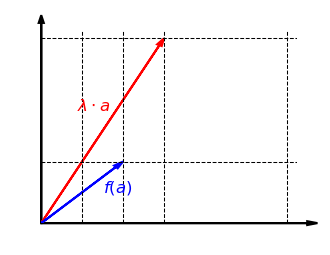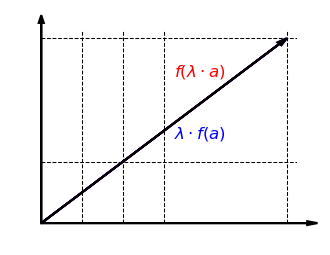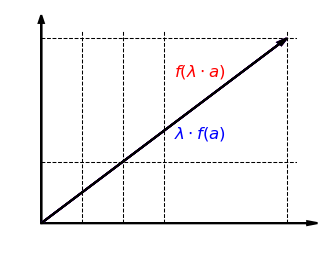
我们考虑函数
例如,函数
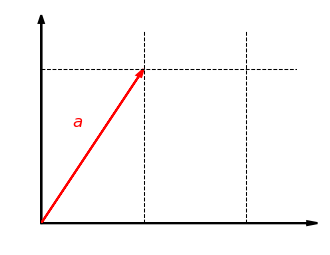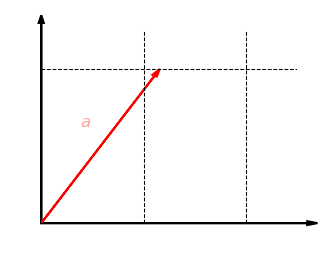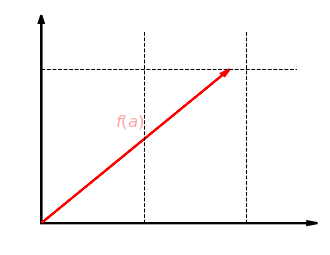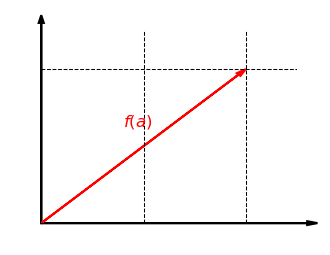
这个函数

函数
2凯莱与矩阵
阿瑟·凯莱(Arthur Cayley)被公认为矩阵论的奠基人。他表明,先前研究的用于二次形式和线性变换的系数阵列是其一般概念的特例。矩阵代数是在凯莱 1855 年左右的研究工作发展而来的。凯莱研究了线性变换的复合,并由此定义了矩阵乘法,以便复合变换的系数矩阵
首先,凯莱将一个

它是一个数字阵列,对应如下线性方程组,

用矩阵改写上面的线性方程组,
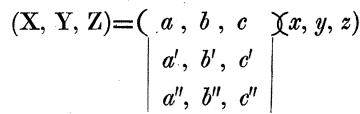
也可以这么来看,将如下 3 个线性函数

改为矩阵形式(注意,此处还没有向量的概念)

上面 3 个函数其实就是 3 个数,分别用大写的
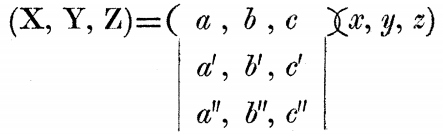
凯莱认为,这个公式蕴含了矩阵理论中的很多基本概念。从现在的角度看,这就是
接着,我们来看两个线性变换的复合,
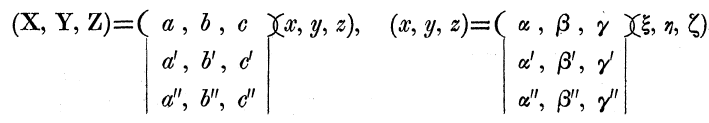
这两个线性变换分别从

复合线性变换对应的矩阵是,

那么这些数字具体是多少呢?将线性方程组的公式代入很容易得到,
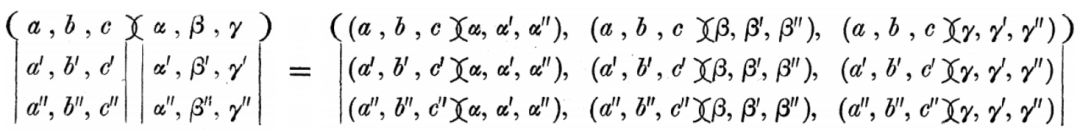
以上就是两个矩阵复合的规则,也是我们现在线性代数书上定义的矩阵乘法。要注意的是,该运算一般情况下是不可交换的,说明线性变换的复合是跟次序有关系的。
可以看到,凯莱把线性方程组看成线性变换,提取出矩阵并从复合线性变换的角度定义矩阵乘积。
用矩阵表示线性变换,这不仅开启了矩阵代数,甚至某个角度也可以说为群表示论啥的埋下了种子。
3定义与实例
我们来看两个向量空间之间的线性变换(或线性映射,线性函数或线性算子)的基本定义。
注意,有些资料会说向量空间到自身的映射叫变换,但这里我们并不采用这种说法。
定义
令
均成立时,
向量空间
例子
令
定义
线性变换的矩阵表示
具有特定基底的向量空间之间的线性变换可以方便地以矩阵形式表示。具体来说,假设
然后,矩阵
换一句话说,可以用矩阵
表示线性变换
其中
是
任意向量
由于
实例解析
看下面的图,假设这是一个将 2D 平面映射到 3D 空间中某个平面的线性映射。

映射
那么请问,在两个空间的自然基底下,这个线性映射可以用一个矩阵表示。那么,请问这个矩阵是?
可见,这个矩阵就是由两列
打个比方,映射就好比红娘,专门为两个空间里的某些向量牵线找对象。我们只要给 2D 平面的自然基底
稍微发散一下,这里有很大空间可以发挥你的想象力。
例如,给
假如,2D 平面的基不取自然基底,而是其他基,如一组标准正交基
4与 SVD 的联系
用矩阵表示,自然就是将一个空间中的某个向量在某组基下的坐标,然后通过矩阵-向量乘法将其转换为另一个空间中的向量坐标。
即用矩阵表示坐标向量之间的转换,如
我们考虑上文中那个将 2D 平面映射到 3D 空间中某个平面的线性映射。
矩阵
对于任意向量
由于
此时,这个线性映射的矩阵非常简单,那就是一个对角矩阵
好了,从这个例子可以看到: 可以用矩阵表示两个线性空间之间的变换,而矩阵的 SVD 分解给出了两个空间的特殊的基底,从而简化这个线性变换的矩阵形式。
这就是矩阵 SVD 分解的巧妙之处,关于它,这里点到为止,具体内容以及相应图解将在后期展开。
