关于黎曼积分的思考——谈黎曼积分的定义观念
日期:2020年08月15日
正文共:6569字1图
预计阅读时间:17分钟
作者:beerht
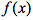 在[a,b]上的一切不连续点成一零测度集”,这里的关键词是“测度”,因此首要的关键问题在于何为“测度”?传统意义上的测度有长度、面积、体积等,我们试图猜测一下,测度的抽象意义可以如何来描述?
在[a,b]上的一切不连续点成一零测度集”,这里的关键词是“测度”,因此首要的关键问题在于何为“测度”?传统意义上的测度有长度、面积、体积等,我们试图猜测一下,测度的抽象意义可以如何来描述?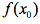 获得了
获得了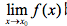 的存在形式(前提是该极限存在),而回归到定义域上则有,由此可知从区间极限的角度来看,抽象数位置处的振幅实际上是实体数收敛的结果。参照“无穷”的广义抽象数形式的定义,所谓收敛,实际上是一个实体数集合的运动能够映射到一个半径极限为0的邻域,所谓发散,即该集合的映射产物是一个半径极限非0的邻域。
的存在形式(前提是该极限存在),而回归到定义域上则有,由此可知从区间极限的角度来看,抽象数位置处的振幅实际上是实体数收敛的结果。参照“无穷”的广义抽象数形式的定义,所谓收敛,实际上是一个实体数集合的运动能够映射到一个半径极限为0的邻域,所谓发散,即该集合的映射产物是一个半径极限非0的邻域。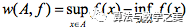
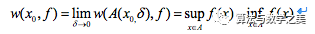
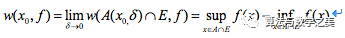
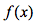 在点
在点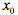 处连续等价于
处连续等价于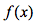 在该点振幅为0”来试验一下这种观点的优势
在该点振幅为0”来试验一下这种观点的优势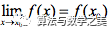 ,则对任意
,则对任意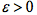 ,必然存在
,必然存在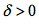 ,满足
,满足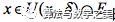 时,均有
时,均有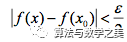 ,则易知
,则易知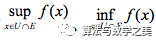 也服从此规律,因此对任意
也服从此规律,因此对任意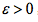 有
有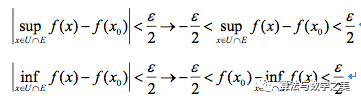
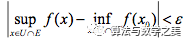 ,由此可知连续是振幅为0的充分条件。
,由此可知连续是振幅为0的充分条件。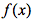 定义域内。
定义域内。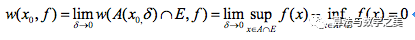
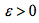 ,均存在
,均存在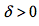 ,满足
,满足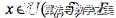 时,,由振幅定义可知
时,,由振幅定义可知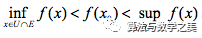 ,则对于
,则对于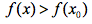 ,则有
,则有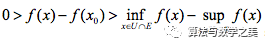 ,而对于,则有,于是有
,而对于,则有,于是有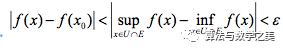 因此连续
因此连续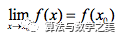 ,中等式左边的各个代数符号都指代“抽象数”,而等式右边的代数符号则指代“代数值”)。这样做之所以有好处,就是将“连续性”集中于一个“抽象数”点的论证拓展为对一个“实在值”区间内的论证。(这么做其实是很难的,作为质性定义,抽象数往往利于揭示概念本质而短于计算应用,之所以要建立抽象数和实在值的关系,本质上还是为了能够让计算尽量回归到实在值域中来),说白了,从开展分析的角度上讲,极限定义的最大好处是将极限的数值关系内涵说清楚了,而振幅定义的最大好处就是把在一个孤点的连续性问题用“幅度变化”的数值关系指代清楚了。
,中等式左边的各个代数符号都指代“抽象数”,而等式右边的代数符号则指代“代数值”)。这样做之所以有好处,就是将“连续性”集中于一个“抽象数”点的论证拓展为对一个“实在值”区间内的论证。(这么做其实是很难的,作为质性定义,抽象数往往利于揭示概念本质而短于计算应用,之所以要建立抽象数和实在值的关系,本质上还是为了能够让计算尽量回归到实在值域中来),说白了,从开展分析的角度上讲,极限定义的最大好处是将极限的数值关系内涵说清楚了,而振幅定义的最大好处就是把在一个孤点的连续性问题用“幅度变化”的数值关系指代清楚了。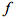 ,若存在任意划分
,若存在任意划分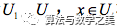 ,均有
,均有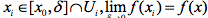 ,则称
,则称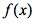 在x上的测度。若上式对任意
在x上的测度。若上式对任意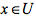 均成立,则称
均成立,则称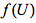 为f在U上的测度。
为f在U上的测度。— THE END —

评论
