变透明的黑匣子：UCLA 开发可解释神经网络 SNN 预测山体滑坡-技术圈

   
    
     
      
       
        本文约3600字，建议阅读10分钟
        
         SNN 具有完全可解释性、高准确性、高泛化能力和低模型复杂度等特点，进一步提高了滑坡风险的预测能力。

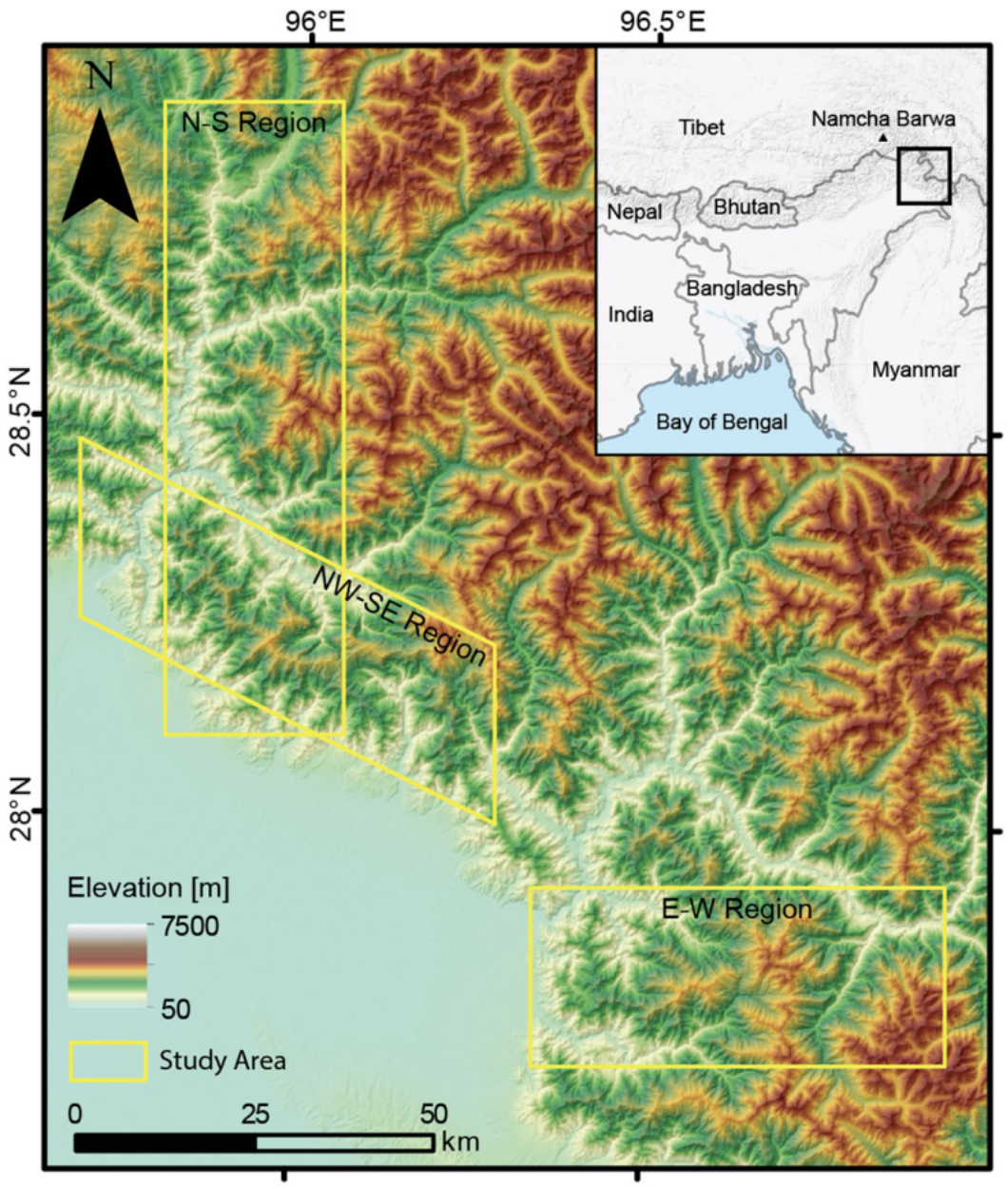
内容一览：由于涉及到多种时空变化因素，山体滑坡预测一直以来都非常困难。深度神经网络 (DNN) 可以提高预测准确性，但其本身并不具备可解释性。本文中，UCLA 研究人员引入了 SNN。SNN 具有完全可解释性、高准确性、高泛化能力和低模型复杂度等特点，进一步提高了滑坡风险的预测能力。

山体滑坡的发生受到多种因素的综合影响，如地形、坡度、土壤、岩石等物质特征，以及气候、降雨、水文等环境条件。因此，相关预测一直以来都非常困难。通常情况下，地质学家使用物理和统计模型来估计滑坡发生的风险。虽然这些模型可以提供相当准确的预测，但训练物理模型需要大量的时间和资源，并不适合大规模应用。

近年来，研究人员一直在训练机器学习模型用于预测山体滑坡，特别是深度神经网络 (Deep Neural Network, DNN)。DNN 作为一个高精度预测模型，在图像识别、语音识别、自然语言处理、计算生物、金融大数据等多个领域效果显著，但它输入层和输出层之外有多层隐藏结构，缺乏可解释性，这种黑盒问题一直困扰着研究人员。

近期，加利福尼亚大学洛杉矶分校 (UCLA) 的研究人员开发了一种可叠加神经网络 (Superposable Neural Network，SNN)。与 DNN 不同，SNN 可以将不同数据输入的结果分开，更好地分析自然灾害中的影响因素。SNN 模型在性能上优于物理和统计模型，并且达到了与最先进 DNN 相似的性能。目前，该研究成果已发表在《Communications Earth & Environment》期刊上，标题为《Landslide susceptibility modeling by interpretable neural network》。

图 1：该研究成果已发表在

《Communications Earth & Environment》

阅读完整论文：

https://www.nature.com/articles/s43247-023-00806-5#Sec4

选取喜马拉雅山最东部滑坡数据

研究人员通过数据分析发现，2004-2016 年山体滑坡造成人员伤亡的情况集中发生在亚洲。喜马拉雅山最东部地区极易发生陡坡滑坡、极端降水、洪水等事件。 研究人员通过将手动划定滑坡区域与半自动检测算法相结合，生成了喜马拉雅山最东部的滑坡清单（滑坡事件的记录或数据集）。在整个 4.19 × 109 平方米的研究区域内，测绘滑坡总数为 2,289 处，面积范围为 900 至 1.96 × 106 平方米。

图 2：喜马拉雅山最东部的研究区域

颜色代表海拔，黄色框表示 N-S (Dibang)、NW-SE（range front）和 E-W (Lohit) 方向的研究区域。

插图表示喜马拉雅东部地区，黑框表示研究区域，深灰色线表示国家边界（右上角）。

如上图所示，研究人员在喜马拉雅山最东部选择了 3 个环境条件不同的地区（Dibang, Lohit 和 range front）测试 SNN 模型的性能和应用。下文中，Dibang、Lohit 和 range front 地区分别被称为 N-S、E-W 和 NW-SE。

数据集地址：

https://doi.org/10.25346/S6/D5QPUA

模型开发：6 步训练一个 SNN

本研究中，为了在保证精确度的同时，规避 DNN 缺乏可解释性问题，研究人员结合模型提取 (model extraction) 和基于特征的方法，生成了一种完全可解释的 additive ANN 优化框架。Additive ANN 是广义加性模型 (generalized additive models, GAM) 的一种。模型提取方法旨在训练一个可解释的 student 模型来模仿 teacher 模型。基于特征的方法旨在分析和量化每个输入特征的影响。

研究人员将这种 additive ANN 架构称为 Superposable Neural Network (SNN) 优化。不同于 DNN 是通过不同层之间的连接来建立特征之间的相互依赖关系，SNN 是通过原始输入特征的乘积函数来建立特征之间的相互依赖关系，两者间的对比如下图所示：

图 3：传统 DNN vs. SNN

x1，x2，...，xn 表示一组 n 个原始特征，χ1，χ2，...，χM 表示一组 M 个组合特征，Y 和 St 分别指 DNN 和 SNN 中的易发性结果。

如图 3 所示，在传统 DNN 中，特征通过网络中的连接来表示和学习，这种依赖关系紧密嵌入在网络结构中，十分复杂并且难以分离。而在 SNN 中，研究人员事先找到并明确地将有助于输出的特征独立输入，每个神经元仅与一个输入相连。

SNN 训练流程图如下：

图 4：训练 SNN 流程图

图中显示，研究人员采用了两个主要方法，特征选择模型 (feature-selection model) 和多阶段训练 (multistage training)。特征选择模型用于选择最相关的特征进行后续分析和建模；多阶段训练则指训练过程分为多个阶段，每个阶段都有特定目标和训练策略，逐步优化模型性能。

训练流程可总结为以下步骤：

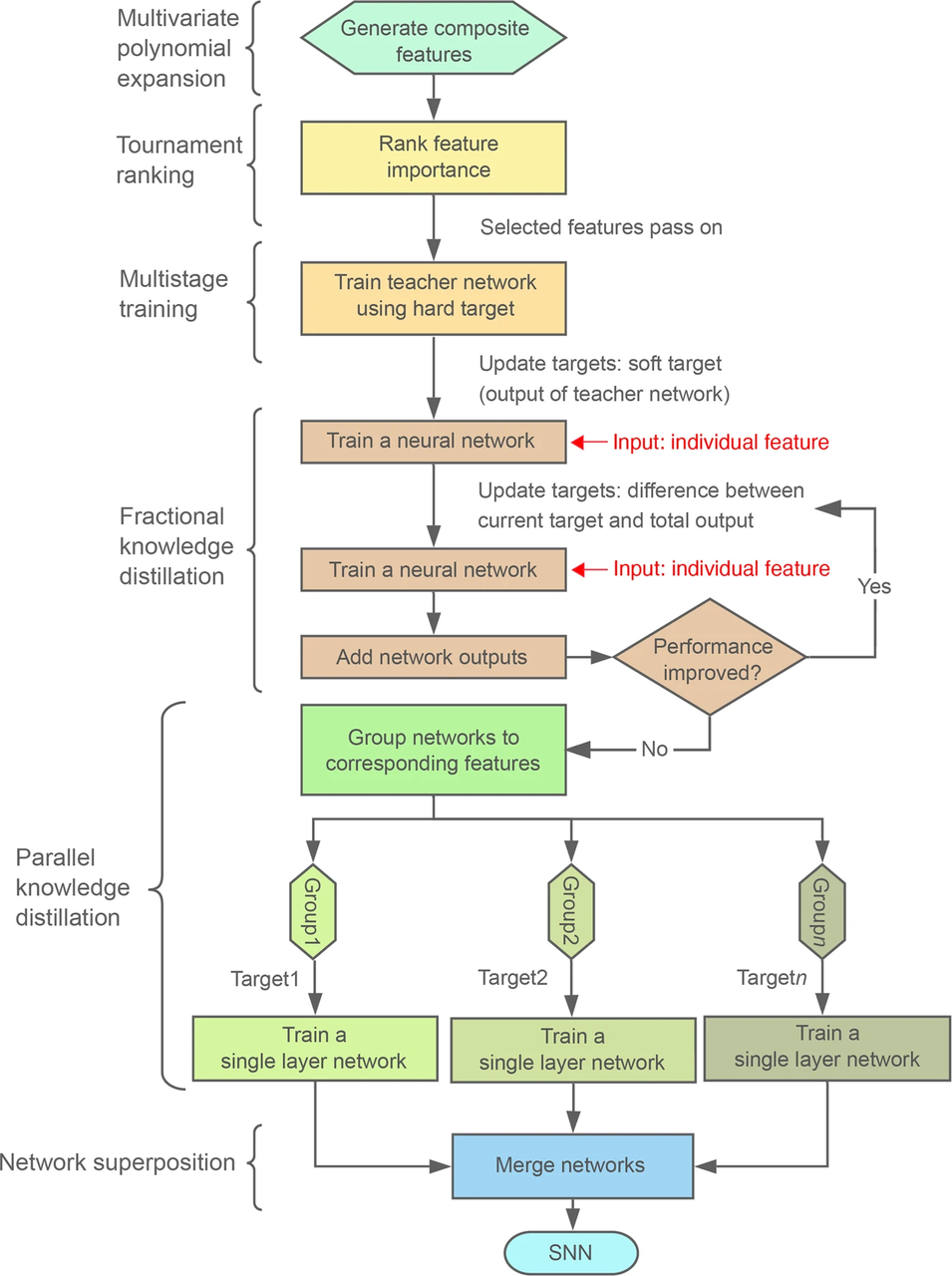
多元多项式展开 (Multivariate polynomial expansion)：生成复合特征。
锦标排名 (Tournament ranking)：一种自动特征选择方法，用于找出与模型最相关的特征。
多阶段训练 (MST)：一种二阶深度学习技术，用于生成高性能的 teacher 网络。
分数知识蒸馏(Fractional knowledge distillation)：用于分离每个特征对最终输出的贡献。
并行知识蒸馏(Parallel knowledge distillation)：将标准的知识蒸馏技术单独应用于与每个特征对应的网络。
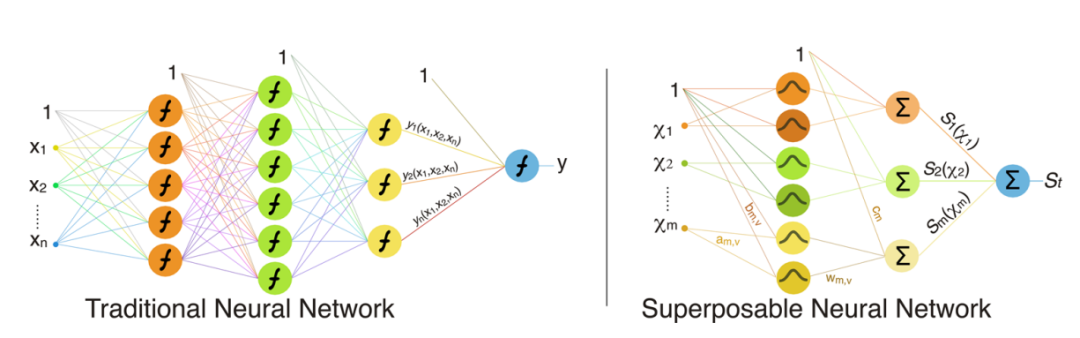
网络叠加 (Network superposition)：将与每个特征对应的单层网络合并成一个 SNN。

实验结果

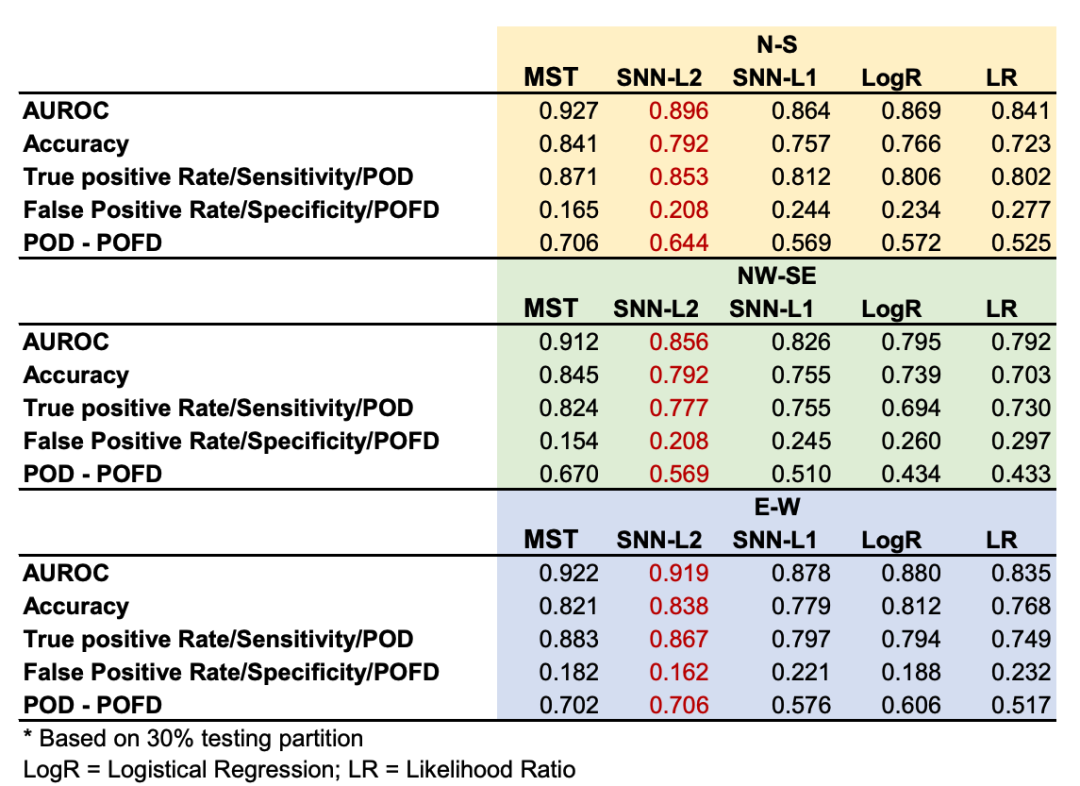
SNN 最高准确率超 99%

根据模型训练中使用的最高级别的复合特征，研究人员将 SNN 分为 3 个不同级别的模型，即 Level-1、Level-2 和 Level-3。实验表明，Level-3 SNN 准确率能达到 SOTA teacher DNN 的 99% 以上，Level-2 SNN 准确率则超过 98%。考虑到两者间准确率的差距很小，研究人员假设 Level-2 SNN 的可解释性对于分析来说是足够的。

接下来研究人员将 Level-1 和 Level-2 SNN 与 SOTA DNN teacher 模型（MST，基于二阶优化的 DNN），以及传统方法（LogR 及 LR）进行比较，所有方法均应用于相同的区域并使用相同的数据，结果如下图所示。

图 5：各模型性能对比

MST: SOTA DNN Teacher 模型

LogR: 逻辑回归（传统方法）

LR: 似然比（传统方法）

如图所示，SNN 与 MST 模型性能相当，且优于常用的传统模型。3 个研究区域的平均值计算，Level-1 和 Level-2 SNN 的 AUROC 分别为 0.856 和 0.890。Level-2 SNN 的 AUROC 比 LogR (AUROC = 0.848) 和 LR (AUROC = 0.823) 高出约 8%。

AUROC (area under the receiver operating characteristic): 用于评估分类模型的性能指标。AUROC 越接近 1，模型性能越好。

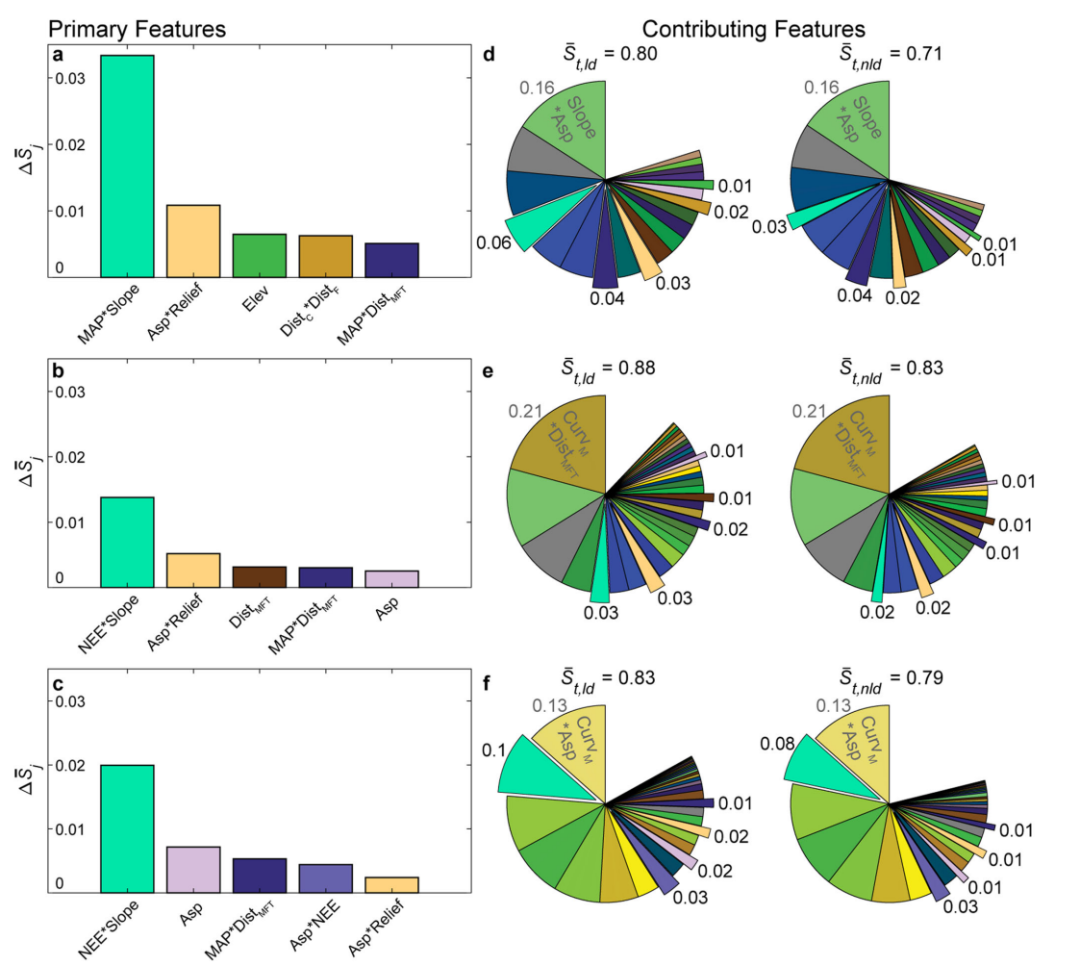
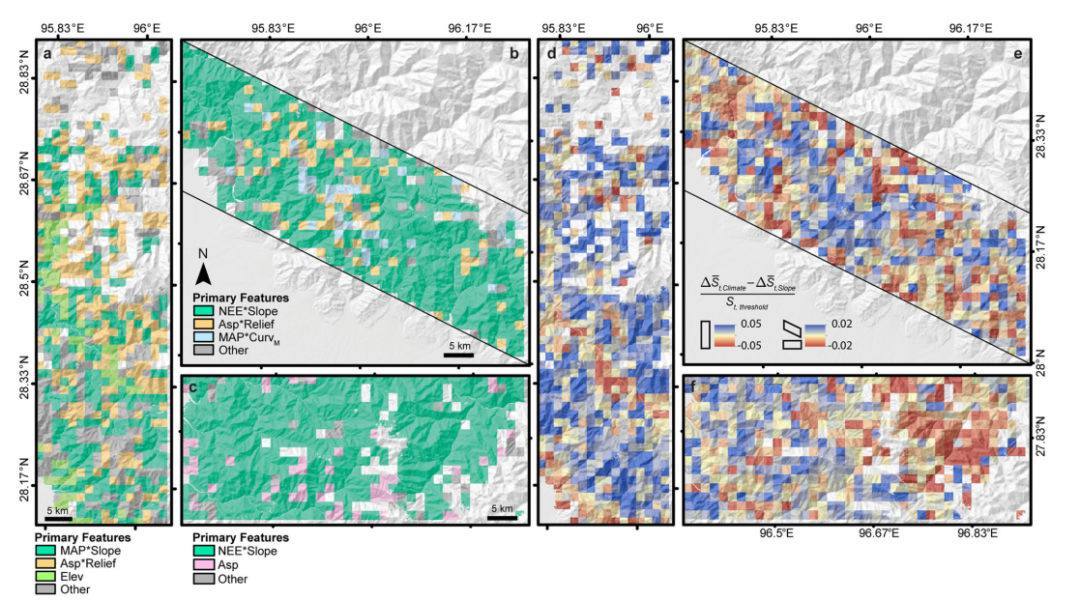
SNN 具备完全可解释性

SNN 是一个完全可解释的模型，其可解释性水平可与线性回归相媲美。

研究人员将研究区域分为滑坡 (ld) 和非滑坡(nld) 区域。SNN 提供了个体特征对易发性的确切贡献，使量化各特征对滑坡易发性的影响成为可能。通过计算个体特征在 ld 与 nld 区域间的差异，可以确定滑坡的主要控制因素及其相对贡献。

如下图所示，MAP*Slope（平均年降水量和斜坡的乘积）、NEE*Slope（极端降雨事件数量和斜坡的乘积）、Asp*Relief（坡向和局部送风的乘积）及 Asp（坡向）在所有三个区域中都有较大的影响。

图 6：各特征对滑坡易发性的影响

(a, d): N-S 研究区域；(b, e): NW-SE 研究区域；(c, f): E-W 研究区域。

(a–c) 中的条形图按降序表示各特征在滑坡 (ld) 和非滑坡 (nld) 区域中的差异大小；(d–f) 中的饼图表示各特征对滑坡 (ld) 和非滑坡 (nld) 区域的平均影响。

平均年降水量 (MAP)、极端降雨事件数量 (NEE)、坡向 (Asp)、海拔 (Elev)、平均曲率 (CurvM)、到河道的距离 (DistC)、所有断层 (DistF) 和主锋面逆冲和裂缝带(DistMFT)，以及局部送风 (Relief)。

星号 * 表示两个特征的代数乘法。

由于 SNN 独有的能力，研究人员可以分离出主要控制特征的空间分布及其局部影响。

图 7：各特征空间分布

a-c: 主要特征的空间分布。

d-f: 气候与坡度对易发性的影响。

(a, d): N-S 研究区域；(b, e): NW-SE 研究区域；(c, f): E-W 研究区域。

气候影响较大的地方呈蓝色，坡度影响较大的地方呈红色。

平均年降水量 (MAP)、极端降雨事件数量 (NEE)、坡向 (Asp)、海拔 (Elev)、平均曲率 (CurvM)、局部送风 (Relief)。

星号 * 表示两个特征的代数乘法。

如上图 d-f 所示，在 N-S、NW-SE 及 E-W 区域中，分别大约 74%、54% 和 54% 的地点受气候特征（如极端降雨事件数量、平均年降水量和坡向）的影响程度大于坡度的影响程度，在图中表现为蓝色面积大于红色，表明了气候特征在控制喜马拉雅最东部地区山体滑坡的重要性。由于沿喜马拉雅山脉向东降水率逐渐增加，喜马拉雅山脉东部地区垂直气候变化显著。这种气候梯度很可能影响喜马拉雅山脉东部地区的滑坡易发性。

SNN 代码 GitHub 地址:

https://GitHub.com/geosnn/geosnn.git

SNN 突破滑坡预测难题

本研究作者 Louis Bouchard 和 Seulgi Moon 都是 UCLA 的副教授，Khalid Youssef 在 UCLA 进行博士后研究，Kevin Shao 为 UCLA 地球、行星和空间科学博士研究生。

图 8：从左到右依次为 Louis Bouchard, Seulgi Moon, Khalid Youssef, Kevin Shao

Kevin Shao 谈到「深度神经网络 (DNN) 可以提供准确的滑坡发生可能性，但无法确定哪些具体的变量会引起滑坡发生及其原因。」共同第一作者 Khalid Youssef 指出「问题在于 DNN 的各个网络层在学习过程中不断相互影响，因此将其结果分析清楚是不可能的。该研究希望能够清楚地将不同数据输入的结果分离出来，使其在确定影响自然灾害的最重要因素方面更加有用。」

「类似于用尸检来确定死因，确定滑坡的确切触发因素总是需要田野测量和土壤、水文和气候条件的历史记录，如降雨量和强度，这些数据在像喜马拉雅山脉这样的偏远地区很难获取。但是 SNN 可以确定关键变量并量化它们对滑坡易发性的贡献。」 Seulgi Moon 教授说到。Louis Bouchard 则表示「不像 DNN 需要强大的计算机服务器来进行训练，SNN 的体积小到可以在苹果手表上运行。」

研究人员计划将他们的工作拓展到世界上其他容易发生滑坡的地区，例如加利福尼亚州。在加州，频繁的山火和地震导致滑坡风险加剧，而 SNN 可以帮助开发早期预警系统，综合考虑多种信号并预测其他一系列地表危险。

参考文章：

[1]https://phys.org/news/2023-06-geologists-artificial-intelligence-landslides.html

[2]https://newsroom.ucla.edu/releases/artificial-intelligence-can-predict-landslides

[3]https://www.bccn3.com/news/ucla-geologists-develop-ai-model-to-predict-landslides

[4]https://static-content.springer.com/esm/

art%3A10.1038%2Fs43247-023-00806-5/MediaObjects/43247_2023_806_MOESM1_ESM.pdf

编辑：黄继彦