如何通过K-means进行人群聚类？

01

—

和层次聚类不同的是，K-means聚类不是把样本一个一个聚集起来，而是对整体样本空间进行分割。因此，K-means聚类属于分割法的一种。

在聚类前，我们首选需要预置一个划分的数量，即k。然后进行k个区间的划分。目标是找到k个族群的划分方式，最终使得划分后的族群内的方差最小。

具体步骤如下：

• 步骤一：选定k个“种子”样本，作为初始的族群代表；
  

• 步骤二：把每个样本归入到距离最近的种子所在的族群；

• 步骤三：归类完成后，将新产生的族群的质心定为新的种子；

• 步骤四：重复步骤2和3，直到不需要移动
  

以上则完成了一个K-means聚类的全过程。

如何确定初始值K

了解了上面的步骤，细心地朋友肯定要有疑问，初始值k如何进行确定呢？即应该聚类成几类才是最合理的？

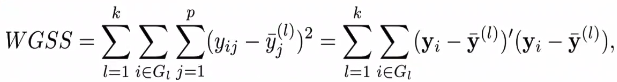
上面的公式是族群内的方差和。我们的目标是使得方差足够小，但又不能是最小。因为其实当k=n时，达到最小，但这种聚类是相当于没有聚类了。

那该如何判断k的取值，使得方差足够小呢？

我们先来看看聚类数量和WGSS的关系，即如下的“碎石图”：

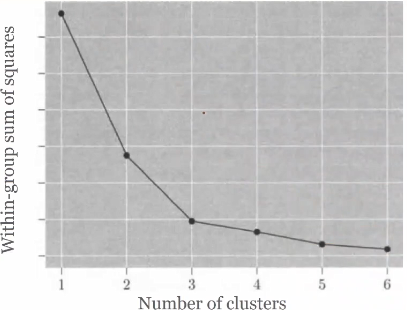
从这个图看的话，我们取k=3比较合适。因为在k=3的时候，族群内的方差和，下降的足够快，而再往后，基本没有太多的下降，也就意味着更多的族群没有太大的意义了。

初始种子的选取

另外，初始种子的选取其实也是很重要的，并不是随机选择k个就万事大吉了。为啥呢？

我们看一下下面的例子。

我们想对（a）图的样本进行聚类。很容易观测，若是在左下角和右上角分别取一个初始种子，应该可以很快完成最终（f）的聚类结果。

但是，如果选了（b）图的两个种子，可就比较“费劲”了，虽然最后也会达成（f）的效果，但是明显要经历更多的迭代过程。

因此，初始种子的选取，对于快速达成结果，是有着重要的意义的。更别说，有时初始种子选的不好，可能最后并不能达成全局最优的聚类结果。比如下图：

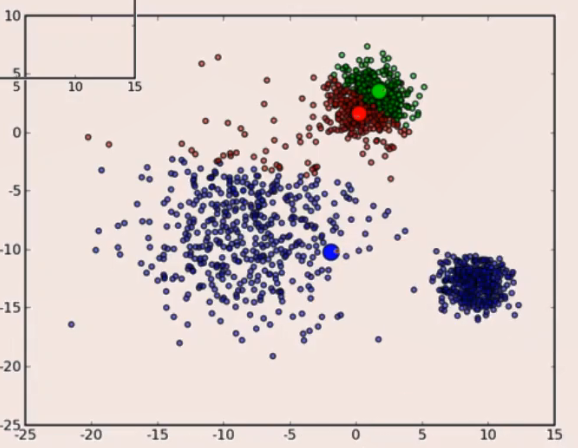
上面的例子中，初始的三个种子，有两个种子选在了上面的一个族群中，最终的结果就是无论怎么迭代，都无法将右下角的族群，分离出来了。

那具体有哪些方法能最大限度避免上面种子选取的问题呢？

• 方法一：在相互间隔超过某指定最小距离的前提下，随机选取k个个体；

• 方法二：选择数据集前k个相互距离超过某指定最小距离的个体；
  

• 方法三：选择k个相互距离最远的个体；
  

• 方法四：选择k个等距网格点，可能不是数据集的点