【机器学习】xgboost系列丨xgboost原理及公式推导

建树过程中如何选择使用哪个特征哪个值来进行分裂? 什么时候停止分裂? 如何计算叶节点的权值? 建完了第一棵树之后如何建第二棵树? 为防止过拟合,XGB做了哪些改进
树的集成

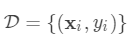 ,其中
,其中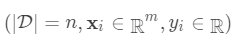 。
。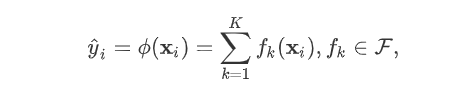
为子模型的预测函数,每个
即是一棵树。
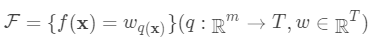 即树的搜索空间。其中q为每棵树的结构,q将
即树的搜索空间。其中q为每棵树的结构,q将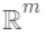 域中每个样本对应到唯一的叶节点上,最终产生T个叶节点,
域中每个样本对应到唯一的叶节点上,最终产生T个叶节点,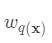 则是该叶节点对应的权重,w即从节点到权重的映射(权重即叶节点的值)。每个
则是该叶节点对应的权重,w即从节点到权重的映射(权重即叶节点的值)。每个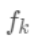 对应一个独立的树结构q和该树每个叶节点的权重w。(这里树结构是指每个分裂点和对应的分裂值)。
对应一个独立的树结构q和该树每个叶节点的权重w。(这里树结构是指每个分裂点和对应的分裂值)。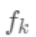 可以看做一个分段函数,q对应的不同的分段,w对应的为该分段的值,
可以看做一个分段函数,q对应的不同的分段,w对应的为该分段的值,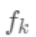 即分段到值的映射。
即分段到值的映射。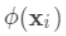 ,目标函数为:
,目标函数为: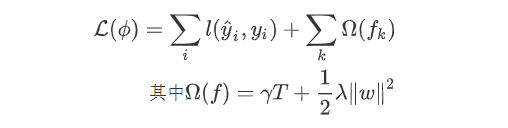
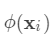 ,其参数为一个个的函数
,其参数为一个个的函数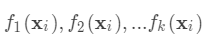 ,因为参数为函数,所以
,因为参数为函数,所以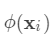 无法使用传统的优化方法在欧氏空间中进行优化,而是采用了加法模型来进行训练。
无法使用传统的优化方法在欧氏空间中进行优化,而是采用了加法模型来进行训练。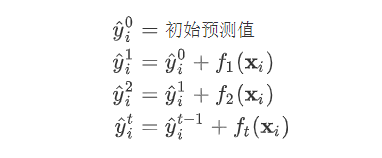
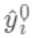 (对应xgboost中参数base_score,注意并不等于base_score,而是经过Sigmoid函数映射后的值),在此基础上根据该预测值与真实y值的损失 ,建立第一棵树
(对应xgboost中参数base_score,注意并不等于base_score,而是经过Sigmoid函数映射后的值),在此基础上根据该预测值与真实y值的损失 ,建立第一棵树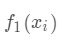 ,之后每次迭代时都是根据其之前所有树做出的预测之和与真实y值的损失来建立新树。也就是每次迭代建树时用新树
,之后每次迭代时都是根据其之前所有树做出的预测之和与真实y值的损失来建立新树。也就是每次迭代建树时用新树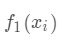 来优化前一个树的损失 。
来优化前一个树的损失 。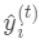 为第t棵树对第i个样本做出的预测。我们每次添加新树的时候,要优化的目标函数为上一个树产生的损失。
为第t棵树对第i个样本做出的预测。我们每次添加新树的时候,要优化的目标函数为上一个树产生的损失。
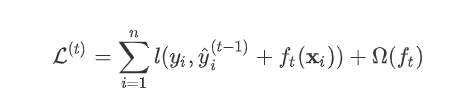
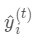 为新建的这棵树做出的预测,
为新建的这棵树做出的预测,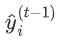 为之前所有的树预测值之和,
为之前所有的树预测值之和,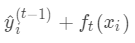 即是新建了当前这棵树后模型做出的预测值,求其与真实值
即是新建了当前这棵树后模型做出的预测值,求其与真实值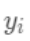 之间的损失(注意这里是损失不是残差,这里的
之间的损失(注意这里是损失不是残差,这里的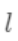 可以是log_loss, mse等)。
可以是log_loss, mse等)。
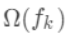 。gbdt对损失函数的优化是直接使用了损失函数的负梯度,沿着梯度下降的方向来减小损失,其是也就是一阶泰勒展开。而xgboost在这里使用了二阶泰勒展开,因为包含了损失函数的二阶信息,其优化的速度大大加快。
。gbdt对损失函数的优化是直接使用了损失函数的负梯度,沿着梯度下降的方向来减小损失,其是也就是一阶泰勒展开。而xgboost在这里使用了二阶泰勒展开,因为包含了损失函数的二阶信息,其优化的速度大大加快。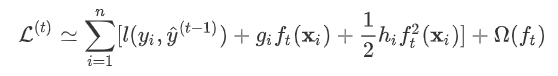
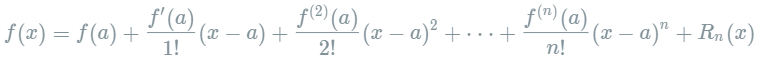 其中的多项式称为函数在a处的泰勒展开式,剩余的
其中的多项式称为函数在a处的泰勒展开式,剩余的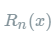 是泰勒公式的余项,是
是泰勒公式的余项,是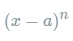 的高阶无穷小。
的高阶无穷小。 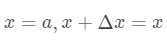 可以得到二阶展开式:
可以得到二阶展开式: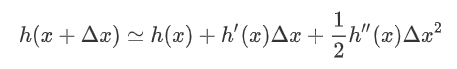
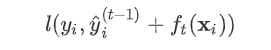
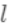 为预测值
为预测值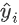 和真实值
和真实值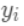 之间的损失,
之间的损失,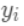 为常量,因此
为常量,因此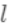 是以预测值
是以预测值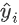 为自变量的函数,当建立新树给出新的预测
为自变量的函数,当建立新树给出新的预测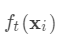 后,相当于在上一次的预测
后,相当于在上一次的预测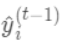 上增加了一个无穷小量
上增加了一个无穷小量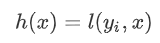
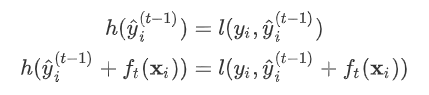
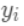 是常数,
是常数,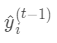 是上次迭代求出的值即这里的
是上次迭代求出的值即这里的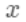 ,
,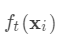 为无穷小量
为无穷小量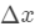 。有了这个对应之后。
。有了这个对应之后。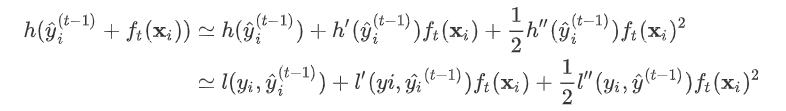
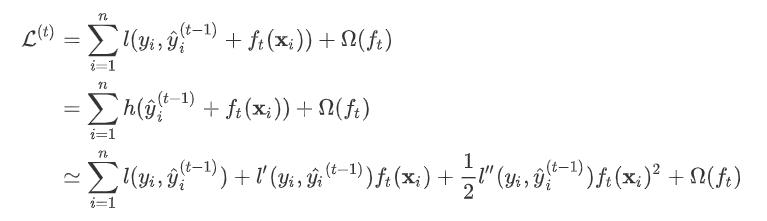
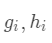 ,其中
,其中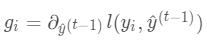 ,
,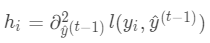
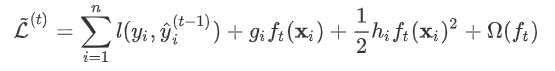
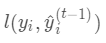 为常量,优化的是损失函数的最小值,因此常量值可以从损失函数中去掉。上式可简化为:
为常量,优化的是损失函数的最小值,因此常量值可以从损失函数中去掉。上式可简化为: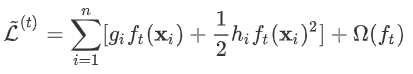
叶节点权重

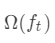 进行展开,得:
进行展开,得: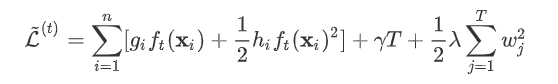
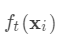 是新建的树的值,对于每个样本来说,就是对应的叶节点的权重
是新建的树的值,对于每个样本来说,就是对应的叶节点的权重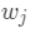 。定义
。定义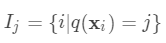 为分到叶节点
为分到叶节点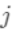 的样本(叶节点总数为T,样本总数为n)
的样本(叶节点总数为T,样本总数为n)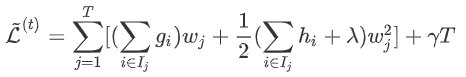
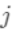 上的损失:
上的损失: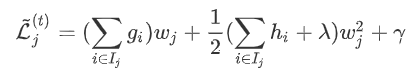
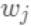 使
使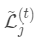 最小,显然这是个一元二次方程求最小值问题。
最小,显然这是个一元二次方程求最小值问题。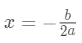
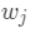 的最优值:
的最优值: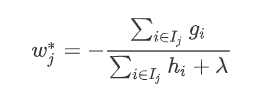
分裂准则

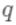 )在此权重下对应的的最小损失为每个叶节点上样本最小损失之和(将上式中的
)在此权重下对应的的最小损失为每个叶节点上样本最小损失之和(将上式中的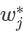 代入):
代入):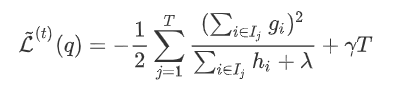
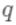 下产生的最优损失
下产生的最优损失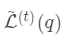 可以做为树结构的评价函数,也就是作为树分裂时候的评价指标。
可以做为树结构的评价函数,也就是作为树分裂时候的评价指标。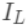 为每次分裂时分到左子树上的样本,
为每次分裂时分到左子树上的样本,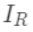 为每次分裂时分到右子树上的样本,有
为每次分裂时分到右子树上的样本,有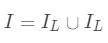 。则在该次分裂后损失的减小量为:
。则在该次分裂后损失的减小量为: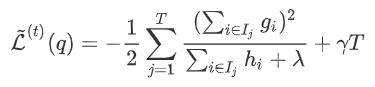
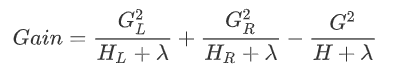
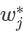 是使函数达到解析解的权重
是使函数达到解析解的权重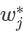 。
。
损失函数计算

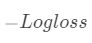 :
: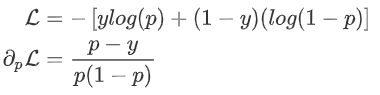
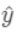 为预测值,则有:
为预测值,则有: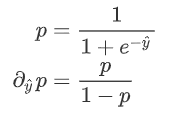
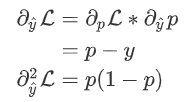
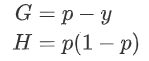

往期精彩回顾
获取本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/qFiUFMV
本站qq群704220115。
加入微信群请扫码:
评论
