【炼丹】深度学习多目标优化的多个loss应该如何权衡

看了那么多篇理论慢慢的paper，终于找到一篇比较有工程意义的paper了。

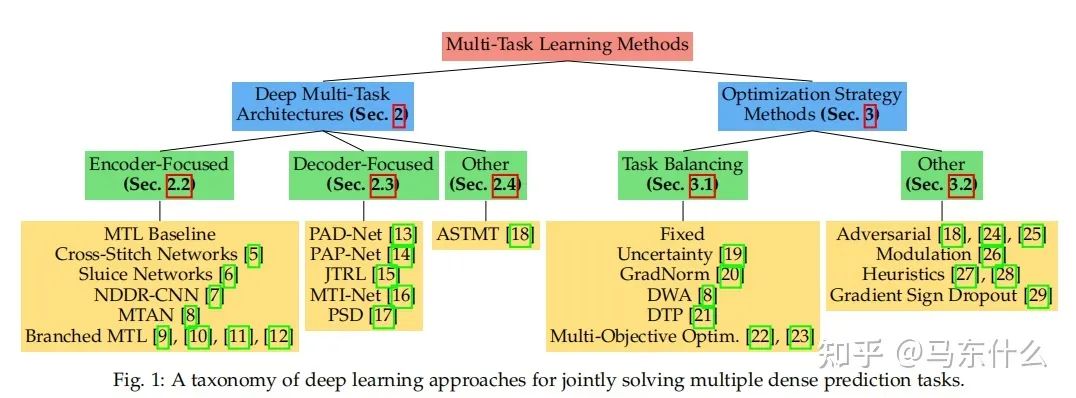
对于应用来说，这样比较简单直接的survey才是王道啊！感觉之前看的多任务的survey公式和定理太多，还是这样的文章比较能够帮助快速上手解决问题。

当然这里主要还是介绍optimization strategy部分。

这篇文章提到了多任务学习的两个主要研究方向：

1、多任务学习的网络结构的构造；

2、多任务学习对标的多目标优化的方法；

大体上分为两种：

1、task balancing；

2、others。。。。

MTL中的一个重大挑战源于优化过程本身。特别是，我们需要仔细平衡所有任务的联合训练过程，以避免一个或多个任务在网络权值中具有主导影响的情况。极端情况下，当某个任务的loss非常的大而其它任务的loss非常的小，此时多任务近似退化为单任务目标学习，网络的权重几乎完全按照大loss任务来进行更新，逐渐丧失了多任务学习的优势（具体优势可见：

马东什么：多任务学习之非深度看起来头大的部分

https://zhuanlan.zhihu.com/p/361464660

马东什么：多任务学习之深度学习部分

https://zhuanlan.zhihu.com/p/361915151

第一大类方法 Task Balancing Approaches

假设任务特定权重的优化目标wi和任务特定损失函数Li：

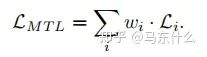
当使用随机梯度下降来尽量减少上图方程的总目标函数值（这是深度学习时代的标准方法），对共享层Wshare中的网络权值通过以下规则进行更新：

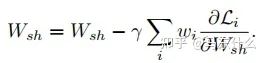
从上图的方程可以看出：

1、loss大则梯度更新量也大；

2、不同任务的loss差异大导致模型更新不平衡的本质原因在于梯度大小；

3、通过调整不同任务的loss权重wi可以改善这个问题；

4、直接对不同任务的梯度进行处理也可以改善这个问题；

所以，后续的方法大体分为两类：

1、在权重wi上做文章；

2、在梯度上做文章

在权重上做文章的方法：

1、Uncertainty Weighting

https://arxiv.org/pdf/1705.07115v3.pdf

人工定义多任务loss的权重是之前主要的使用方法，这种方法存在许多问题。模型性能对权重的选择非常敏感，如图所示。

横轴和纵轴分别是两个任务的权重，曲线上的点对应不同权重下多任务深度学习网络最终的训练结果。

这些权重作为超参数调整起来非常的费事费力，每次测试通常需要很多的时间。

在贝叶斯学习

https://book.douban.com/subject/26284941/

关于python概率编程非常推荐这本书，这本也有中文版：

贝叶斯方法：概率编程与贝叶斯推断

另外，tensorflow-probability在google上有关于这本书完整的代码demo，非常浅显易懂，上手快。

另外也有torch版的pyro

相关的代码可见：

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

https://github.com/tensorflow/probability

https://github.com/pyro-ppl/pyro

中，认为模型存在两种不确定性：

张子杨：【实验笔记】深度学习中的两种不确定性（上）

https://zhuanlan.zhihu.com/p/56986840

1.偶然不确定性
我们初高中学物理的时候，老师肯定提过偶然误差这个词。我们做小车下落测量重力加速度常数的时候，每次获得的值都会有一个上下起伏。这是我们因为气流扰动，测量精度不够等原因所造成的，是无法被避免的一类误差。在深度学习中，我们把这种误差叫做偶然不确定性。
从深度学习的角度来举例子，我们举一个大家应该很比较熟悉的人脸关键点回归问题[3]:

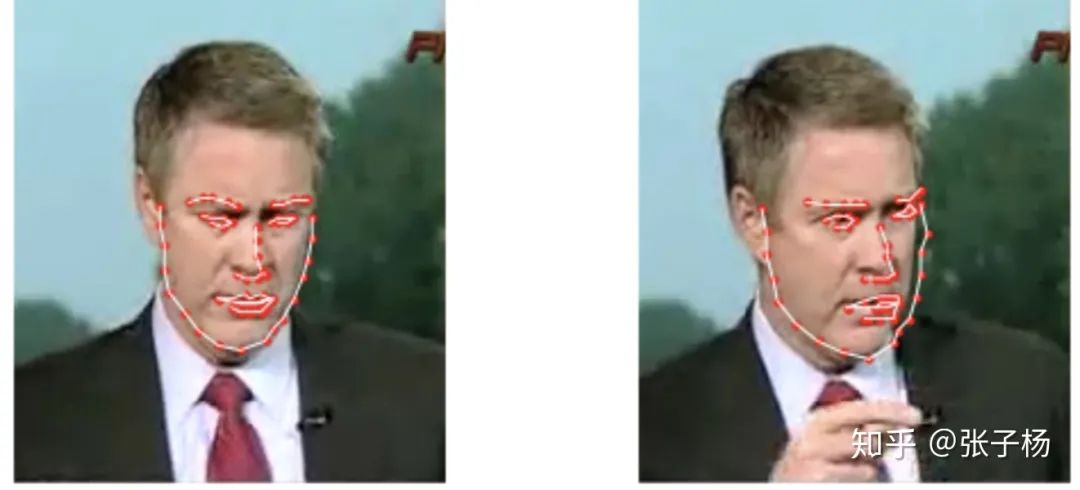
我们可以看到，对于很相似的一组数据，dataset的标注出现了比较大的误差（见右图的右侧边缘）。这样的误差并不是我们模型带入的，而是数据本来就存在误差。数据集里这样的bias越大，我们的偶然不确定性就应该越大。

2.认知不确定性
认知不确定性是我们模型中存在的不确定性。就拿我们文章一开始举的例子来说，假设我们训练一个分类人脸和猩猩脸的模型，训练中没有做任何的增强，也就是说没有做数据集的旋转，模糊等操作。如果我给模型一个正常的人脸，或者是正常猩猩的脸，我们的模型应该对他所产生的结果的置信度很高。但是如果我给他猫的照片，一个模糊处理过得人脸，或者旋转90°的猩猩脸，模型的置信度应该会特别低。换句话说，认知不确定性测量的，是我们的input data是否存在于已经见过的数据的分布之中。

认知不确定性可以通过增加更多的data来缓解，偶然不确定性则需要对数据进行统一标准的处理。

偶然不确定性又存在两种不确定性类别：

（补充：异方差和同方差，以经典的线性回归为例，我们常常假设线性回归的误差项满足同方差，即误差项的方差是相同的，如果不相同则为异方差，一个比较形象的例子：

什么是异方差？为什么异方差的出现通常与模型中某个解释变量的变化有关？

https://www.zhihu.com/question/354637231/answer/895286217

1 数据依赖性（异方差不确定性）依赖于输入数据，模型预测结果的残差的方差即随着数据的输入发生变化；

2、任务依赖性（同方差不确定性）是不依赖于输入数据的任意不确定性，它与模型输出无关，是一个在所有输入数据保持不变的情况下，在不同任务之间变化的量，因此，它可以被描述为与任务相关的不确定性，但是作者并没有详细解释在多任务深度学习中的同方差不确定性的严格定义，而是认为同方差不确定性是由于任务相关的权重引起的。

下面我们定义fW(x)为nn的预测值，也就是我们熟悉的y_pred，

对于回归型任务，我们定义下面的不确定性：

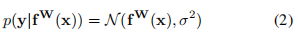
其中  在代码中的体现，是一个可学习的参数，我们用这个参数服从的公式2的高斯分布作为同方差不确定性的衡量方法，即以 y_pred为均值向量，**2 作为方差的多元高斯分布；

对于分类问题有：

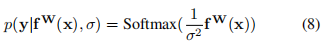
这被称作是Boltzmann分布，也叫做吉布斯分布.

则在多目标的前提下，我们认为总的同方差不确定性可以用不同任务的不确定性的乘积来表示：

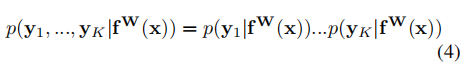
通过对公式（4）进行对数变换后可以得到：

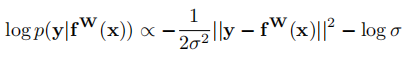
（这个正比的公式是怎么得到的。。。）

现在让我们假设我们的模型输出由两个向量y1和y2组成，每个向量都遵循一个高斯分布：

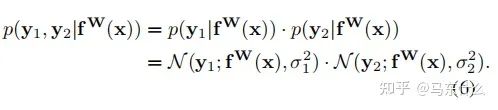
（这里作者没有说清楚，实际上这里作者是假设我们有两个回归型的目标任务，并且损失函数使用的是mse）

然后得到多输出模型的最小化目标函数 L(W、σ1、σ2)：

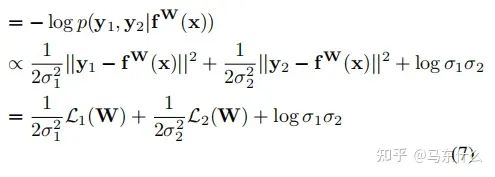
因此，对于公式（7），在新的回归型任务中，我们可以将L1(W)和L2(W)用其它的回归任务对应的损失函数来代替；

对于分类型任务，作者木有给出最终的化简公式，不过对照下面的一个分类型任务+一个回归型任务的化简公式：

这里补充一下公式10的推导部分，具体的近似在上图，将上图带入公式10即可。至于这个近似公式怎么来的，我也没看明白。。。有懂得大佬求指正一下

我们可以先推出单个回归型任务的不确定性度量公式，从而得到分类型任务的同方差不确定性的近似衡量公式为：

和

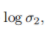
的和。

则也可以如法炮制，比较容易地写出两个分类型任务不确定性的化简公式了，简单来看就是分母少了2.（推导部分太头大了就不看了）

这种构造可以简单地扩展到任意离散和连续损失函数的组合，允许我们以一种有原则和有充分根据的方式学习每一个损失的相对权重。这种损失是平滑可微的，并且分布形状很好，使得任务权重不会收敛到零。相比之下，使用直接学习权值会导致快速收敛到零的权值。

总结一下，整体的思路就是用sigma来衡量同方差不确定性，同方差不确定性和任务有关，同方差不确定性越高的任务则意味着模任务相关的输出的噪声越多，任务越难以学习，因此在多任务模型训练的过程中，其对应的sigma会增大，削弱这类任务的权重使得整体的多任务模型的训练更加顺畅和有效。

在代码实现上有个小问题，也是比较常见的实现和论文存在区别的地方：

yaringal/multi-task-learning-example

https://github.com/yaringal/multi-task-learning-example/blob/master/multi-task-learning-example-pytorch.ipynb

这个是原论文作者的实现：基于两个回归型任务，损失函数mse为前提下得到的

def criterion(y_pred, y_true, log_vars):  loss = 0  for i in range(len(y_pred)):    precision = torch.exp(-log_vars[i])    diff = (y_pred[i]-y_true[i])**2. ## mse loss function    loss += torch.sum(precision * diff + log_vars[i], -1)  return torch.mean(loss)

原文提到了我们直接定义变量，这个变量是log(sigma的)(sigma表示的是方差，也就是下图里面的那个二次项)，这样可以避免loss公式中除0的问题：

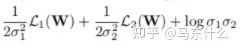
看了一下才发现这是万恶的梯度下降法灵活的变量定义导致的，无论是torch还是tf中，变量为2x还是x都没有区别，因为最终常数项都可以直接融合到变量的求解中，所以之前看的很多的paper的实现里，常数项都是直接包含在变量里省去不写。。真是屑，，，

首先我们定义 log(sigma)=a(a是一个可学习的变量),则 torch.exp(-a)=torch.exp(-log(sigma))=torch.exp(log(sigma**-1))=1/sigma（这里0.5可以省去也可以包含进来，因为我们定义1/2*变量x和直接定义变量x，在梯度下降法求解的过程中没有太大区别，然后是常数项的部分，作者在原文中提到，后面的常数项并不是很重要，放进来作为一种正则乘法太大的sigma（方差），这里后面的常数项，按照代码的意思，是直接用了sigma方差来代替了标准差，其实差别也不大）

所以根据上述的设定对下面的代码做了一些修改：

git上对应的代码：

https://github.com/Mikoto10032/AutomaticWeightedLoss/blob/master/AutomaticWeightedLoss.py

找了几个实现，发现代码都有问题，只有这个git是完全忠于原文的，并且封装的也比较舒服。

import torchimport torch.nn as nn
class AutomaticWeightedLoss(nn.Module):    """automatically weighted multi-task loss    Params：        num: int，the number of loss        x: multi-task loss    Examples：        loss1=1        loss2=2        awl = AutomaticWeightedLoss(2)        loss_sum = awl(loss1, loss2)    """    def __init__(self, num=2):        super(AutomaticWeightedLoss, self).__init__()        params = torch.ones(num, requires_grad=True)        self.params = torch.nn.Parameter(params) #parameters的封装使得变量可以容易访问到
    def forward(self, *x):        loss_sum = 0        for i, loss in enumerate(x):            loss_sum += 0.5 * torch.exp(-log_vars[i]) * loss + self.params[i]# +1避免了log 0的问题  log sigma部分对于整体loss的影响不大        return loss_sum

关于权重项部分

目前看过的三个git上都没有对分类或者是回归的loss区别对待，可以设置参数用于定义分类or回归loss，从而给权重项部分的分布分别赋予回归—2，分类—1。很多作者这部分没有严格按照论文公式来预测，不过上面的code稍微改动一下就可以，但是其实也不用改。。常数项在梯度下降的过程中都会被优化算法考虑进来的。

适配的话：

from torch import optimfrom AutomaticWeightedLoss import AutomaticWeightedLoss
model = Model()
awl = AutomaticWeightedLoss(2)  # we have 2 lossesloss_1 = ...loss_2 = ...
# learnable parametersoptimizer = optim.Adam([                {'params': model.parameters()},                {'params': awl.parameters(), 'weight_decay': 0}            ])
for i in range(epoch):    for data, label1, label2 in data_loader:        # forward        pred1, pred2 = Model(data)          # calculate losses        loss1 = loss_1(pred1, label1)        loss2 = loss_2(pred2, label2)        # weigh losses        loss_sum = awl(loss1, loss2)        # backward        optimizer.zero_grad()        loss_sum.backward()        optimizer.step()

这种方法的一个比较核心的问题也比较明显吧：

1、同方差不确定性衡量的定义方式是否合理；

2、如果在多任务学习中，我们主要是希望主任务的效果好，辅助任务的效果可能不是很care，那么如果恰好主任务是同方差不确定性最高的，则使用这种方法可能会削弱主任务的效果，这是最大的问题，因为这种处理的方式针对的是整个多任务模型的总体loss来设计的，无法满足对特定任务的不同程度的需求，因为作者原始的思路是不确定性越高的任务越应该削弱权重，但是反过来想，不确定性越高的任务越难，如果我们反而让模型重点去学习这个任务，是否可以提高模型的能力；

3、 这里没有考虑权重和为1的问题，不过我觉得作者本来也没打算这么做，影响不大，权重之和是否为1并不是问题其实，本来多任务也不一定需要权重为1的设定，另外权重简单做归一化就可以得到权重为1了。。

4、实际应用的一个问题，权重可能会变成负数，导致我们最终的loss变成负数了。。。也就是部分任务对于最终总loss的贡献是负贡献，我认为可能是这部分任务的不确定性太大使得模型训练困难，这个部分我们torch.relu进行截断就可以了

2、Grad Norm

梯度归一化的主要目的在于希望不同任务任务对应的梯度具有相似的大小，从而控制多任务网络的训练。通过这样做，我们鼓励网络以相同的速度学习所有的任务。grad norm本身不focus于不同任务之间的权重，而是将所有任务等同视之，只是希望所有任务的更新能够相对接近从而避免了某个任务收敛了，某个任务还在收敛的路上的问题，这样会导致：

1、模型训练的效率低，最终运行时间由最复杂的任务决定；

2、复杂任务收敛的过程中，简单任务的局部最优权重可能会变差；