高端的ICP点云配准只需要简单MATLAB代码
点击下方卡片,关注“新机器视觉”公众号
视觉/图像重磅干货,第一时间送达
各位大家好久不见,我还是小刘。我一直从事着C++视觉方面的工作,最近被C++/Cmake/PCL弄得不要不要的,配置环境。我又想起了我的老伙计-----Matlab。他应该可以做三维点云的基础工作吧。



 大白话来说就是:对同一个物体进行多次扫描后,会有多个点云数据,然后将两个数据中同一点的点云进行匹配,也就是将两幅点云中相同点的点云放在一起即点云配准。
大白话来说就是:对同一个物体进行多次扫描后,会有多个点云数据,然后将两个数据中同一点的点云进行匹配,也就是将两幅点云中相同点的点云放在一起即点云配准。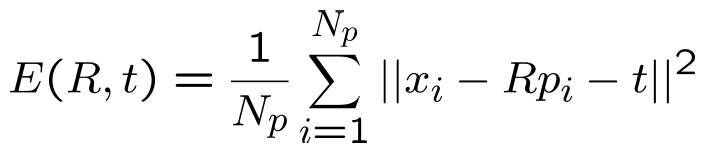
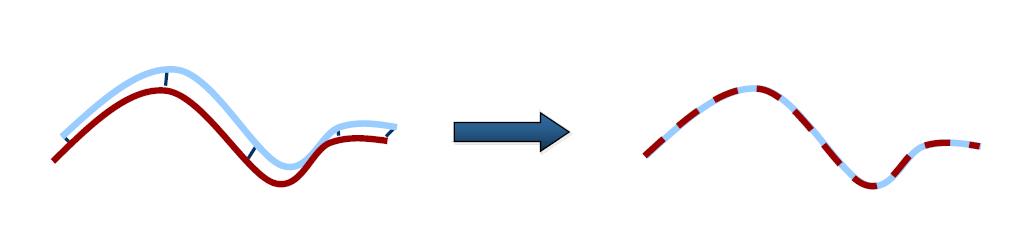
 然后效果就如下图一样,两个条为点云向量,他们属于同一个部位的不同点云集,为了让他们配准在一起,使用算法配准。
然后效果就如下图一样,两个条为点云向量,他们属于同一个部位的不同点云集,为了让他们配准在一起,使用算法配准。
 从一个动图来演示吧:初始是两个不同角度下的笑脸(深红色和绿色),下面是红色笑脸如何通过ICP过程和绿色笑脸重合的:
从一个动图来演示吧:初始是两个不同角度下的笑脸(深红色和绿色),下面是红色笑脸如何通过ICP过程和绿色笑脸重合的:

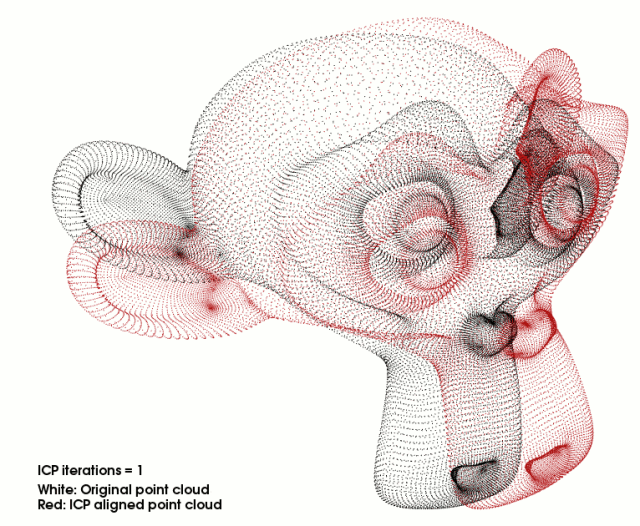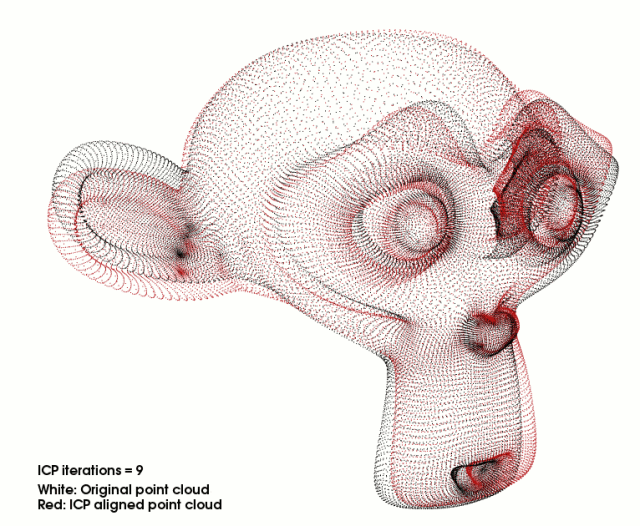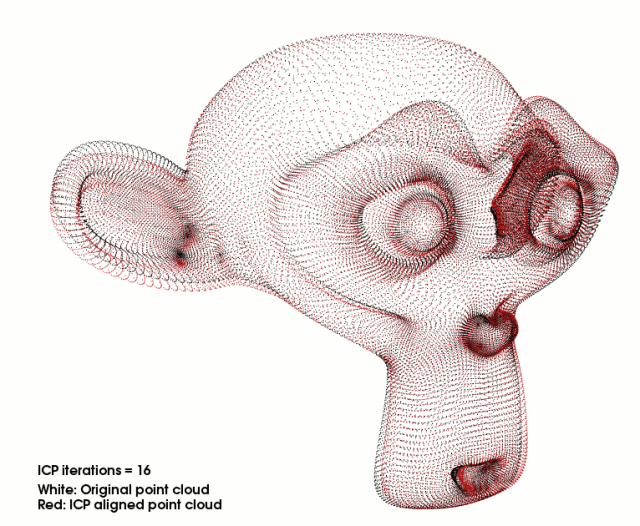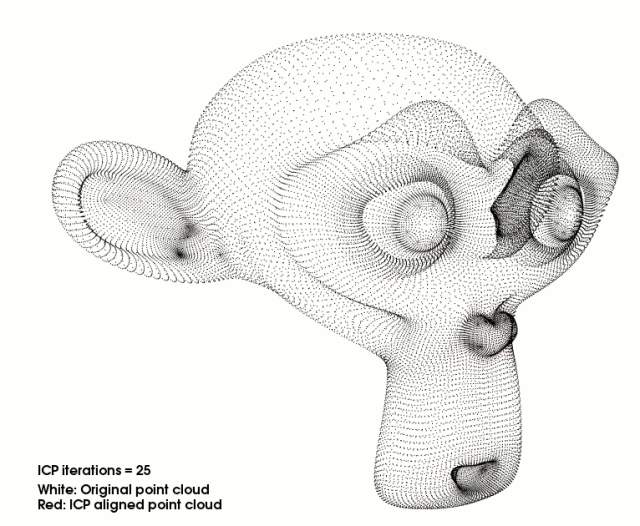
目前应用最广泛的点云精配准算法是迭代最近点算法(Iterative Closest Point, ICP)及各种变种 ICP 算法。
ICP算法流程:
首先对于一幅点云中的每个点,在另一幅点云中计算匹配点(最近点)
极小化匹配点间的匹配误差,计算位姿(旋转矩阵R和平移矩阵t)
然后将计算的位姿作用于点云
再重新计算匹配点
如此迭代,直到迭代次数达到阈值,或者极小化的能量函数变化量小于设定阈值
 1、首先创建两个待配准的点云
1、首先创建两个待配准的点云size1=size(PointCloud1);%点云1if size1(1)==3PointCloud1=transpose(PointCloud1);endsize2=size(PointCloud2);%点云2if size2(1)==3PointCloud2=transpose(PointCloud2);end
两个带配准的点云集
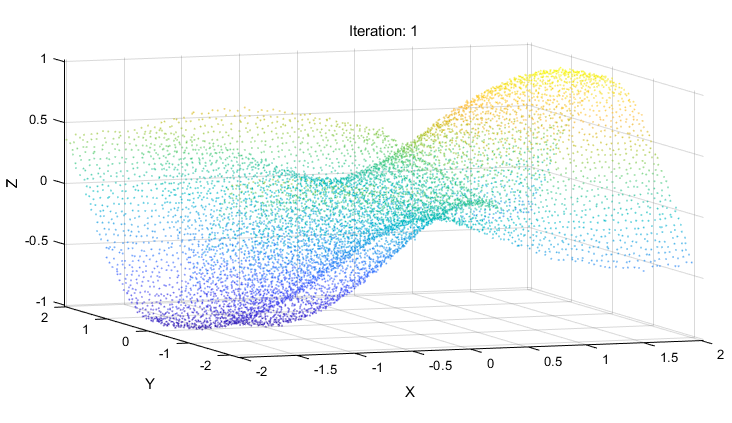
 2.计算距离
2.计算距离
for i=1:size_Psmallest=1e10;correspondence(1,i)=0;for j=1:size_Xdis=(P_iter(1,i)-X_ori(1,j))^2+(P_iter(2,i)-X_ori(2,j))^2+(P_iter(3,i)-X_ori(3,j))^2;if dissmallest=dis;correspondence(1,i)=j;endendendCorre=correspondence;
 3.求解旋转矩阵R和移动矩阵t
3.求解旋转矩阵R和移动矩阵tfunction [t]=GetTranslationVector(P_iter,Xiter_centerPos,R_iter)is 3X3200 Xiter_centerPos is 3X1 R_iter is 3X3Xsum=0;Ysum=0;Zsum=0;size1=size(P_iter);size1=size1(2);for i=1:size1Xsum=Xsum+P_iter(1,i);Ysum=Ysum+ P_iter(2,i);Zsum=Zsum+P_iter(3,i);end=Xsum/size1;=Ysum/size1;=Zsum/size1;t=Xiter_centerPos-R_iter*P_center;end
 4、将计算的位姿作用于点云
4、将计算的位姿作用于点云function [Xcenter]=GetXCenterPos(X_ori,Corre)size_Sum=size(Corre);size_Sum=size_Sum(2);xsum=0;ysum=0;zsum=0;for i=1:size_Sumxsum=xsum+X_ori(1,Corre(1,i));ysum=ysum+X_ori(2,Corre(1,i));zsum=zsum+X_ori(3,Corre(1,i));end=xsum/size_Sum;=ysum/size_Sum;=zsum/size_Sum;end
 5、写一个计算最小误差的函数
5、写一个计算最小误差的函数function [ErrorData]=ComputeErrorMap(corre,P_iter,X_ori)size_P=size(P_iter);size_P=size_P(2);for i=1:size_Px=X_ori(1,corre(i))-P_iter(1,i);y=X_ori(2,corre(i))-P_iter(2,i);z=X_ori(3,corre(i))-P_iter(3,i);err=x^2+y^2+z^2;err=sqrt(err);=err;endErrorData=P_iter;end
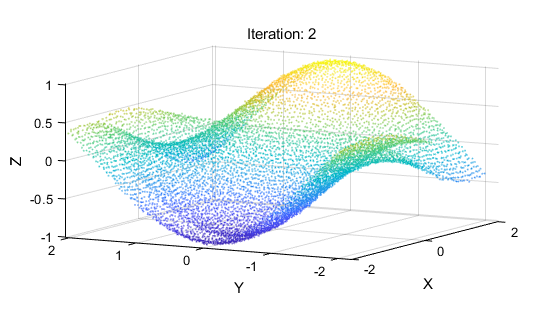
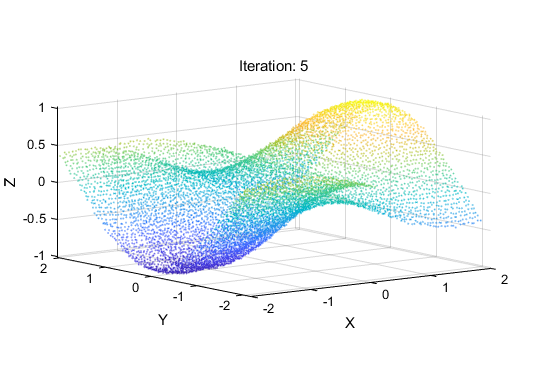
迭代第十次:
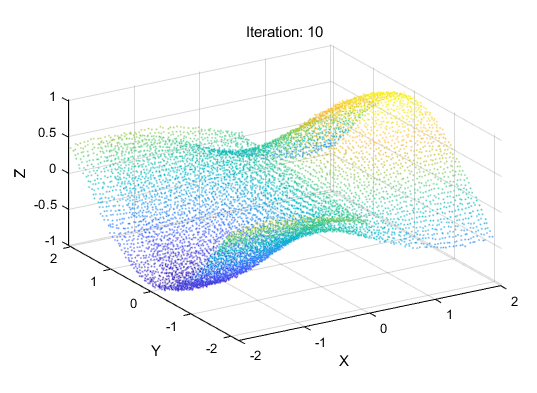
迭代第二十次:
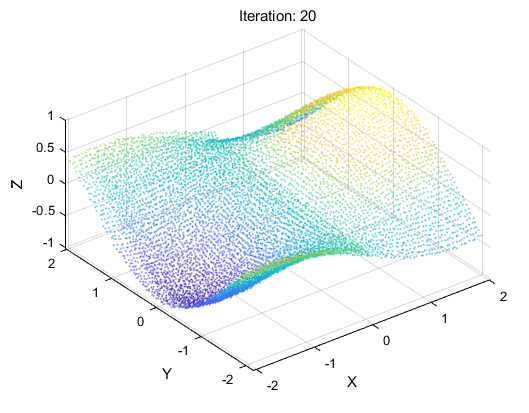
迭代第五十次:我们可以看出两个点云集合几乎重合在一起。
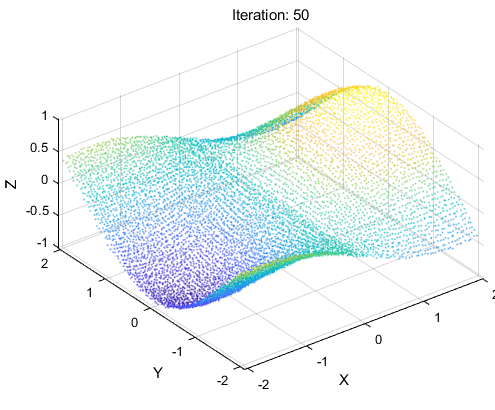
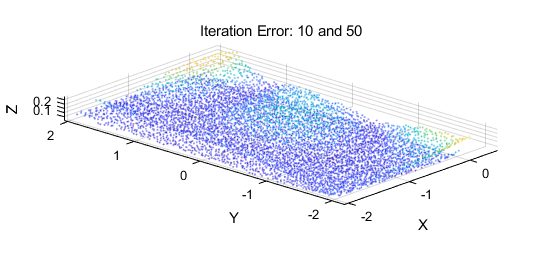
 我猜大家一时半会看不出迭代的差别,那我放一下第十次迭代和最后一次的迭代的误差放出来大家体会一下效果放在一起,看z轴是不是误差越来越小~~
我猜大家一时半会看不出迭代的差别,那我放一下第十次迭代和最后一次的迭代的误差放出来大家体会一下效果放在一起,看z轴是不是误差越来越小~~
 结束语:看来matlab做点云真的不错,不过小刘在写算法的时候,其实觉得matlab用来做算法验证真的不错,不过有一点就是,迭代次数越多,稠密点云的时候会十分的慢,可能这就是脚本语言的通病吧,不过我用了并行加速之后,提升了不少,万物的资本家~~关注我,带你关注更多matlab用法,我们下次再见~
结束语:看来matlab做点云真的不错,不过小刘在写算法的时候,其实觉得matlab用来做算法验证真的不错,不过有一点就是,迭代次数越多,稠密点云的时候会十分的慢,可能这就是脚本语言的通病吧,不过我用了并行加速之后,提升了不少,万物的资本家~~关注我,带你关注更多matlab用法,我们下次再见~
—版权声明—
仅用于学术分享,版权属于原作者。
若有侵权,请联系微信号:yiyang-sy 删除或修改!
