华为提出十大数学挑战！解出一个就是年薪百万！

↑↑↑点击上方蓝字，回复资料，10个G的惊喜

提到香农定理，通信领域的小伙伴应该是非常熟悉的了，可称得上是该领域的「金科玉律」。1948 年，香农博士在《通信的数学原理》一书中提出了这一著名的定理。此后，香农定理成为现代信息论的基础理论，在通信和数据存储领域得到了广泛应用，并为今天通信的发展打下了坚实的理论基础。

信息论之父克劳德 · 香农。

70 多年过去了，通信行业的发展依然离不开基础数学理论的支撑。各大科技公司也纷纷采取自己的方式积极推动数学的发展和吸引数学人才，比如阿里巴巴举办的年度全球数学竞赛等。

华为也不例外。在全球化战略发展中，华为也充分彰显出了其对数学的重视。华为先后在俄罗斯和法国设立了数学研究所，旨在加强基础研究，特别是数学算法方面的研究。这些举措为华为的技术发展提供持续不断的理论源泉。

同样，在国内，华为与众多的数学领军专家开展了深度合作。华为与张平文院士、徐宗本院士、李安民院士都建立了数学联合实验室，并且与高校和科研机构有大量合作课题。

据华为心声社区报道，不久前，在湖南长沙由中国工业与应用数学学会举办的「数学促进企业创新发展论坛」上，华为董事、战略研究院院长徐文伟做了主题为「后香农时代，数学决定未来发展的边界」的演讲，其中谈到了华为对数学的重视，并提出了后香农时代信息产业发展面临的了十大挑战数学问题。

智能社会、5G 与香农极限

徐文伟在演讲中说道，基于七十多年前的香农定理，信息产业才有了五十多年的高速发展，并发明了一代又一代的通信产品。在未来二三十年里，人类社会将进入万物感知、万物互联和万物智能的智能社会，并由此催生新的新的工作、生产和生活模式，这些都与七十年前香农时代发生了根本性的变化。

与此同时，随着社会进入 5G 时代，几乎达到了香农定理的极限。可以说，当前的创新主要是把几十年前的理论成果通过技术和工程来实现。

何谓香农极限？这是通信信道容量在理论上的一个极限值。我们可以先来看下香农第二定律，它表示信道中的极限信息传输率和信道能力，被奉为现代通信的「金科玉律」，公式表示如下：

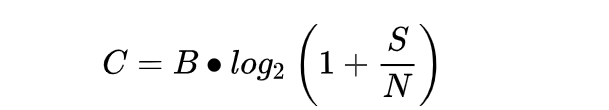
其中 B 表示信道带宽，S/N 表示信噪比，它们成为了决定网速上限的两个基本因素。

根据这一公式，在相同信噪比的情况下，增加信道带宽成为决定 5G 网速的主要因素。对于这种提升信道带宽的方式，有些业内专家称「5G 之后再无 G」，这意味着，未来通信的发展只剩下量的扩增，并无实质的技术进步。

此外，徐文伟还表示，随着智能社会的到来，通信场景由以往的人与人通信为主向人与机器、机器与机器通信为主转换，并相应地出现人与人通信主导的时代没有考虑到的场景和问题。

这些新场景、新问题和新挑战，我们可以称进入了后香农时代。在后香农时代，不仅需要理论的突破和工程技术的发明，更需要数学家们发挥核心作用。

所以，华为发布了后香农时代面向数学的十大挑战问题，包括利用更少的计算和存储资源获得更高的性能、需要暴力计算的场景以及采用数学算法和软件优化等减少资源消耗等等业界难题。

十大数学挑战问题

挑战问题 1：有损压缩的极限问题（语义信息论）。

挑战问题 2：突破信源编码理论，挑战无损信源压缩极限。

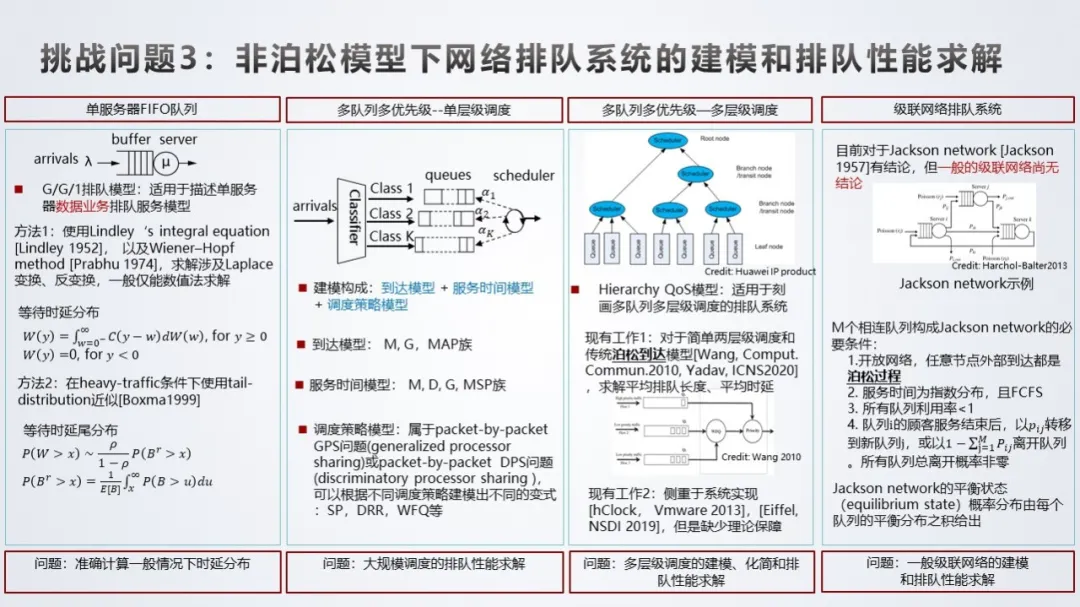
挑战问题 3：网络基本业务模型问题。

挑战问题 4：Massive MIMO 容量域。

挑战问题 5：非线性信道补偿问题。

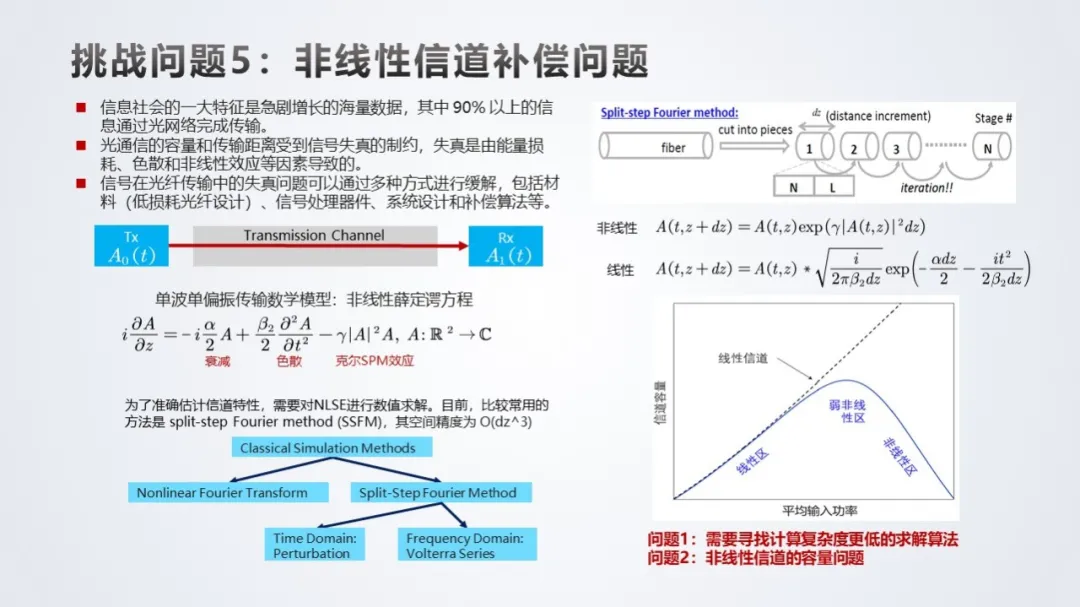
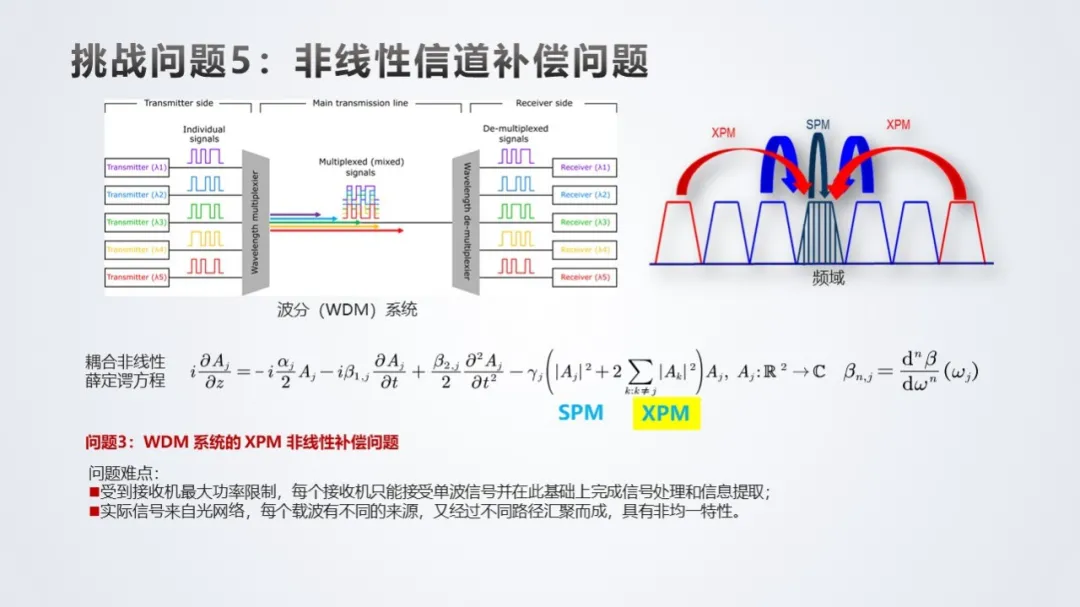
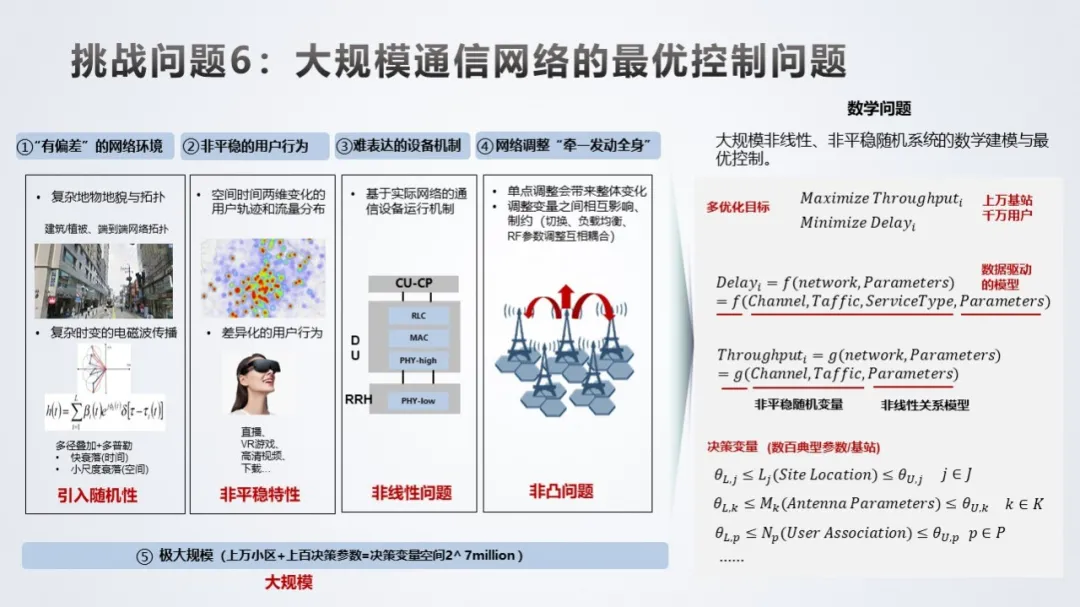
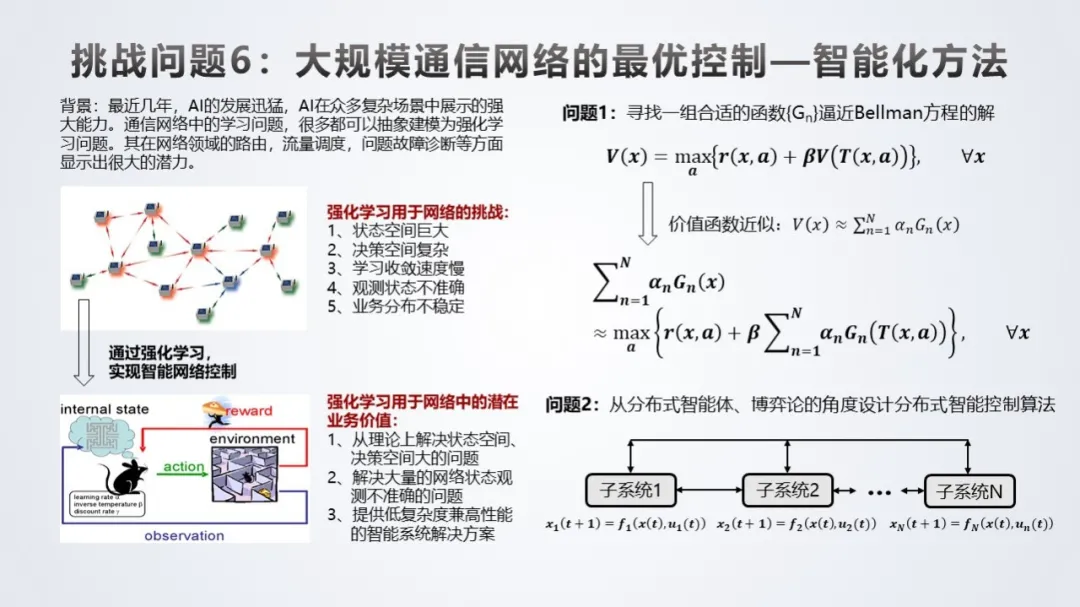
挑战问题 6：大规模通信网络的最优控制问题。

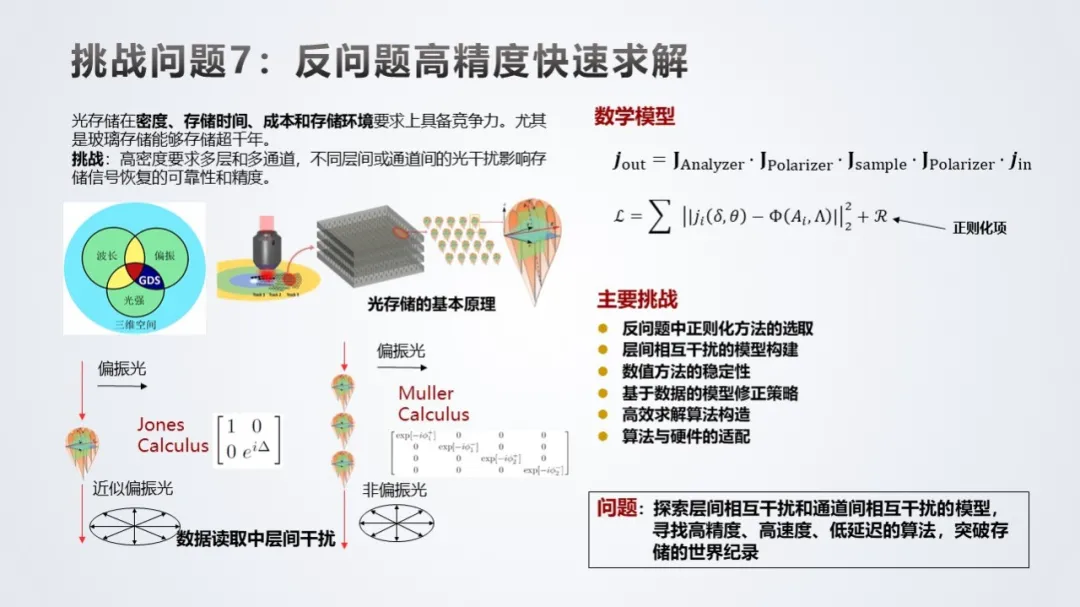
挑战问题 7：反问题高精度快速求解。

挑战问题 8：高性能的纠错码 - 代数几何（AG）码。

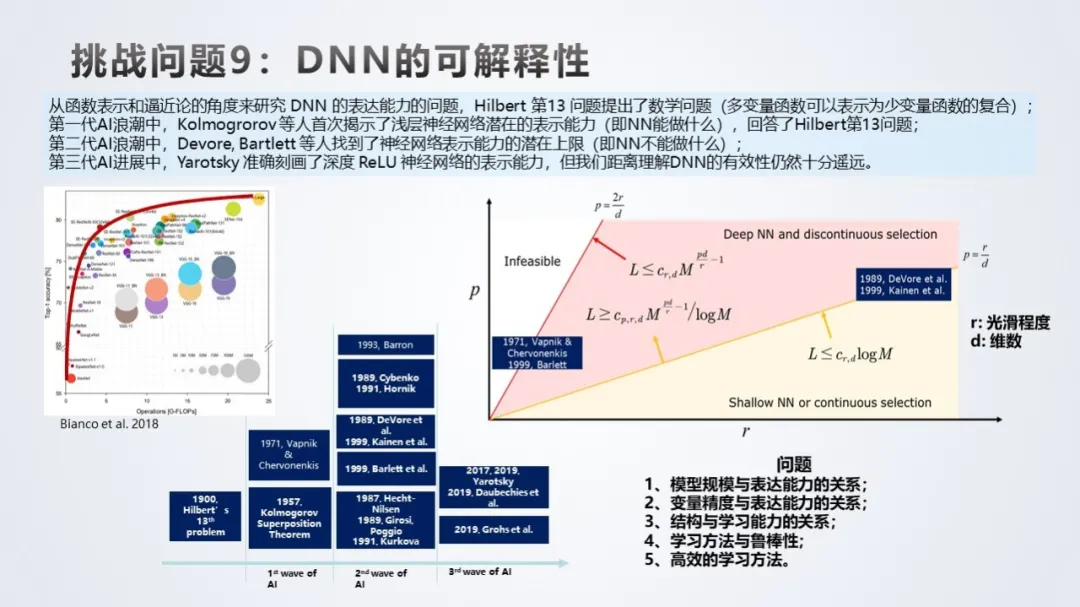
挑战问题 9：DNN 的可解释性。

挑战问题 10：网络级流量矩阵近似计算。

参考链接：

https://mp.weixin.qq.com/s/IfpE-Ynfui4KqO8WynLing

https://www.cnbeta.com/articles/tech/1026255.htm

http://hebei.news.163.com/20/0519/19/FD0UFS8D04159CDF.html

http://www.kepuchina.cn/tech/info/201906/t20190626_1071991.shtml

↓↓↓我的朋友圈更精彩↓

推荐阅读
（点击标题可跳转阅读）
贝叶斯：没有人比我更懂南京市长江大桥
Numpy核心语法和代码整理汇总！
数学系的概率论和我们的不太一样。。。
机器学习模型调参指南（附代码）
老铁，三连支持一下，好吗？↓↓↓