【统计学习方法】第2章感知机课后习题（三）-技术圈

点击上方“公众号”可订阅哦！

“这个公众号在我的新作品中帮助我毫不费力地使用了解决万有引力的问题。我现在有更多时间站在树下，被苹果击中。”

Isaac Newton

本篇文章是课后三个习题。

●

题目：

Minsky 与 Papert 指出：感知机因为是线性模型，所有不能表示复杂的函数，如异或（XOR）。验证感知机为什么不能表示异或。

解答：

首先，来看异或函数的运算，

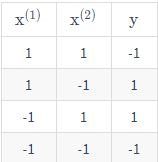
import matplotlib.pyplot as pltimport numpy as npimport pandas as pd%matplotlib inline
x1 = [1, 1, -1, -1]x2 = [1, -1, 1, -1]y = [-1, 1, 1, -1]x1 = np.array(x1)x2 = np.array(x2)y = np.array(y)# np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等。data = np.c_[x1, x2, y]data = pd.DataFrame(data, index=None, columns=['x1', 'x2', 'y'])data.head()
positive = data.loc[data['y'] == 1]negative = data.loc[data['y'] == -1]
plt.xlim(-2, 2)plt.ylim(-2, 2)plt.xticks([-2, -1, 0, 1, 2])plt.yticks([-2, -1, 0, 1, 2])plt.xlabel("x1")plt.ylabel("x2")plt.plot(positive['x1'], positive['x2'], "ro")plt.plot(negative['x1'], negative['x2'], "gx")plt.show()

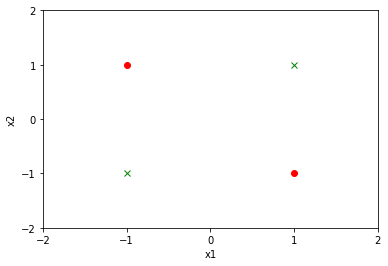
显然，线性不可分。

●

题目：

模仿例题2.1，构建从训练数据集求解感知机模型的例子。

解答：

from sklearn.linear_model import Perceptronimport numpy as np
X_train = np.array([[3, 3], [4, 3], [1, 1]])y = np.array([1, 1, -1])
perceptron_model = Perceptron()perceptron_model.fit(X_train, y)print("w:", perceptron_model.coef_, "\nb:", perceptron_model.intercept_, "\n")
result = perceptron_model.predict(X_train)print(result)

w: [[1. 0.]] b: [-2.] 
[ 1  1 -1]

●

题目：

证明以下定理：样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集所构成的凸壳互不相交。

解答：

略

END

深度学习入门笔记

微信号:sdxx_rmbj

日常更新学习笔记、论文简述

【统计学习方法】 第2章 感知机课后习题（三）

【统计学习方法】第2章感知机课后习题（三）