JZ054-链表中环的入口节点
共 1467字，需浏览 3分钟
·
2021-04-27 19:43
题目描述
题目：给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。
解析思路
链表是由一系列连接在一起的结点构成，其中的每个结点都是一个数据结构。
这道题属于链表题型中等题目，思路如下：
题目未明确给出链表包含环，也就是说我们首先需要判断链表中是否存在环，如果存在然后再计算出环的入口。看到这个题我们直接用快慢指针进行解题：
第一步：定义慢指针p1，快指针p2；
第二步：p1一次走一步，p2一次走两步。直到p1 p2相遇后p2返回链表头结点，然后p2也降为慢指针， p1 p2在同时走；
第三步：p1 p2再次相遇后，返回该Node结点为入环结点；
疑问？
为什么用快慢指针可以判断单链表是否有环。
答：一个指针一次走一步，另一个指针一次走两步。如果走得快的指针追上了走得慢的指针，那么链表就是环形链表；如果走得快的指针走到了链表的末尾（next指向 NULL）都没有追上第一个指针，那么链表就不是环形链表。
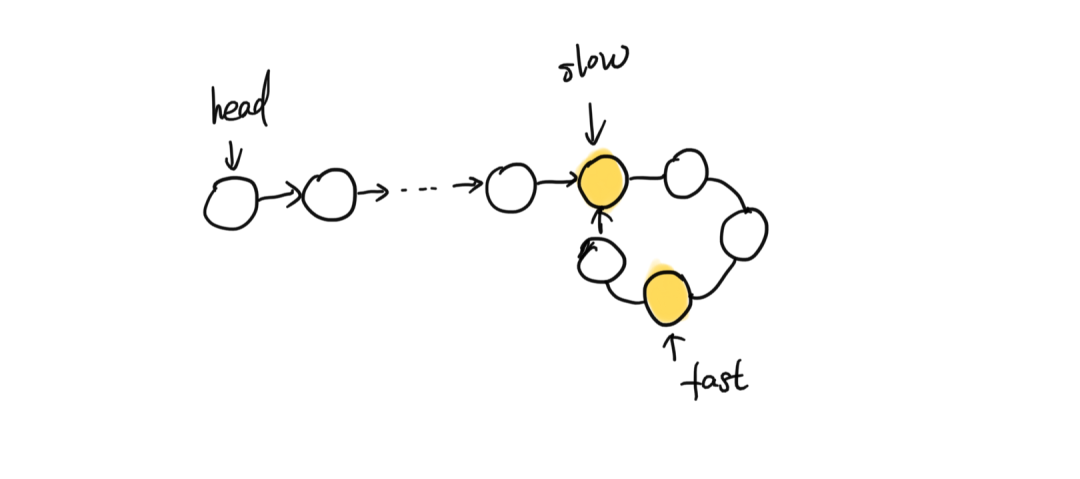
如何判断入口节点呢？
当快慢指针（slow、fast）相遇时，slow指针肯定没有遍历完链表，而fast指针已经在环内循环了n（n>=1）圈。假设slow指针走了s步，则fast指针走了2s步。同时，fast指针的步数还等于s加上在环上多转的n圈，设环长为r，则满足如下关系表达式：
2s = s + nr;
所以可知：s = nr;
假设链表的头节点到“环的尾节点“的长度为L（注意，L不一定是链表长度），环的入口节点与相遇点的距离为x，链表的头节点到环入口的距离为a，则满足如下关系表达式：
a + x = s = nr;
可得：a + x = (n - 1)r + r = (n - 1)r + (L - a)
进一步得：a = (n - 1)r + (L -a - x)
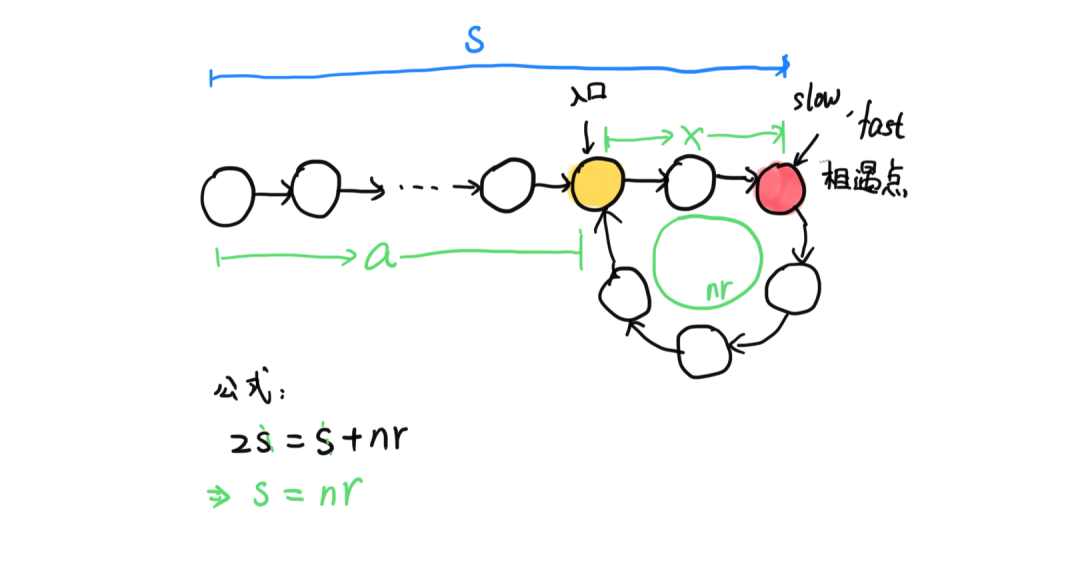
那么可以得出结论：
1. (L - a -x)为相遇点到环入口节点的距离，即从相遇点开始向前移动(L -a -x)步后，会再次到达环入口节点。
2. 从链表的头节点到环入口节点的距离 ＝ (n - 1) * 环内循环 ＋ 相遇点到环入口点的距离。
3. 于是从链表头与相遇点分别设一个指针，每次各走一步，两个指针必定相遇，且相遇第一点为环入口点。
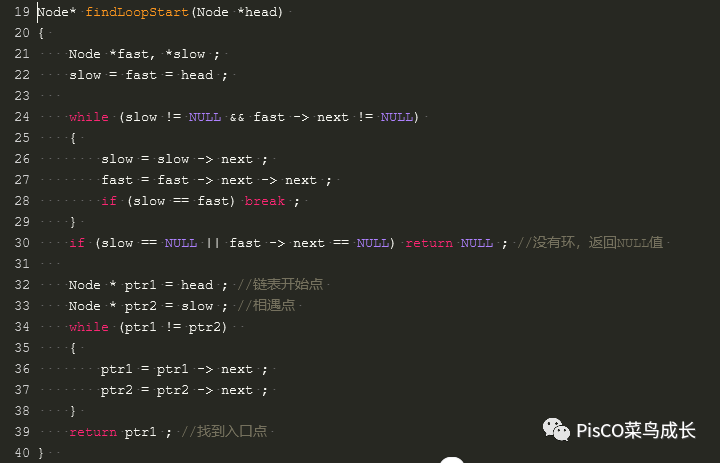
代码Code
判断是否存在环：
求出环的入口：
心得体会
思考为什么他可以写出这么好的代码，把每道题的思路理解后用笔记本记录下来，争取刷到融会贯通，即看见有个题能自动归类到某个方面，这样有一定好处。面试最重要的是让面试官日后能愿意与你以后一起工作，因此沟通交流非常重要。比如有时候面试需要交流，看着像是一道排序的题做不出来，就可以跟面试官交流：“我有几个不成熟的想法，一排序，二动态规划，三是直接搜索算法”，面试官可能就给个提示：“你先用排序试试吧“。
end
往期推荐
点个
在看
你最好看