leetcode必备算法:聊聊滑动窗口
前言
我们刷leetcode的时候,经常会遇到滑动窗口类型题目。滑动窗口问题非常经典,也很有技巧性,一般大厂也喜欢问。今天跟大家一起来学习滑动窗口的套路,文章如果有不正确的地方,欢迎大家指出哈,感谢感谢~
什么是滑动窗口? 一道算法题走进滑动窗口 滑动窗口可以用来解决哪些问题? 滑动窗口框架套路 leetcode案例分析
什么是滑动窗口
滑动窗口这个词,相信大家耳熟能详啦。因为说到TCP的时候,经常谈起滑动窗口协议(Sliding Window Protocol),它是TCP协议的一种应用,用于网络数据传输时的流量控制,以避免拥塞的发生。
TCP头部有个字段叫win,也即那个16位的窗口大小,它告诉对方本端的TCP接收缓冲区还能容纳多少字节的数据,这样对方就可以控制发送数据的速度,从而达到流量控制的目的。
TCP的滑动窗口在某一个时刻就是固定窗口大小的滑动窗口,随着网络流量等因素改变窗口大小也会随着改变。算法中的滑动窗口有点类似,就是维护一个窗口(队列/数组),不断滑动,然后更新答案。滑动窗口,指的是这样一类问题的求解方法,在数组上通过双指针同向移动而解决的一类问题。
一个例子走进滑动窗口算法
我们来看一道算法题吧:给定一个整数数组,计算长度为k的连续子数组的最大总和。
输入:arr [] = {100,200,300,400} k = 2
输出:700
解释:300 + 400 = 700
看到这个题目,我们马上想到暴力法去解决了,两个for搞定:
public int maxSum(int[] arry, int k) {
int size = arry.length;
int maxSum = 0;
for (int i = 0; i < size - k + 1; i++) {
int currentSum = 0;
for (int j = 0; j < k; j++) {
currentSum = currentSum + arry[i + j];
}
maxSum = Math.max(currentSum, maxSum);
}
return maxSum;
}
暴力法用了两个嵌套的for循环,时间复杂度不理想,为O(k*n); 而滑动窗口算法可以解决嵌套循环问题,有效降低时间复杂度。
因为滑动窗口就是维护一个窗口,不断滑动,然后更新答案。 我们用滑动窗口算法来走一波:
当k=2时,
我们可以维护一个长度为2的窗口,初始化第一个窗口值的总和,并保存起来 然后窗口不断向右滑动,滑动过程中,与保存的最大值比较,并更新答案。 窗口直到滑到最右边才结束。
当k=3时,类似的
我们可以维护一个长度为3的窗口,初始化第一个窗口值的总和,并保存起来 然后窗口不断向右滑动,滑动过程中,与保存的最大值比较,并更新答案。 窗口直到滑到最右边才结束。
于是,我们就可以写代码啦:
public int maxSum1(int[] arry, int k) {
int size = arry.length;
if (size < k) {
return -1;
}
//初始化第一个窗口值的总和
int maxSum = 0;
for (int i = 0; i < k; i++) {
maxSum = maxSum + arry[i];
}
int sum = maxSum;
for (int i = k; i < size; i++) {
sum = sum + arry[i] - arry[i - k];
maxSum = Math.max(maxSum,sum);
}
return maxSum;
}
使用了滑动窗口,时间复杂度,只需要O(n)就可以解决啦。
滑动窗口可以解决哪些问题
哪些leetcode的题目,我们可以用滑动窗口去解决呢?
一般情况,子串问题,如什么最小覆盖子串、长度最小的子数组等等,都可以考虑使用滑动窗口算法。比较经典的滑动窗口题目有这些:
无重复字符的最长子串 最小覆盖子串 串联所有单词的子串 至多包含两个不同字符的最长子串 长度最小的子数组 滑动窗口最大值 字符串的排列 最小窗口子序列
都是leetcode的原题,大家可以去leetcode官网找找手感哈。
滑动窗口框架套路
滑动窗口的大致逻辑框架,伪代码如下:
int left =0,right = 0;
while (right < s.size()){
//增大窗口
window.add(s[right]);
right++;
while (window needs shrink){
//缩小窗口
window.remove (s[left]);
left ++;
}
}
基本流程就是酱紫:
首先呢,就是获取原字符串的长度。 接着维护一个窗口(数组、哈希、队列) 窗口一步一步向右扩展 窗口在向右扩展滑动过程,需要判断左边是否需要缩减 最后比较更新答案
我们用这个框架,尝试去解一道leetcode的真题吧。
题目:给定一个字符串 s ,请你找出其中不含有重复字符的最长子串的长度。
实例1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
因为需要判断是否存在重复字符,所以,我们用一个哈希集合(HashSet)来作为窗口
int lengthOfLongestSubstring(String s){
//获取原字符串的长度
int len = s.length();
//维护一个哈希集合的窗口
Set windows = new HashSet<>();
int left=0,right =0;
int res =0;
while(right char c = s.charAt(right);
//窗口右移
right++;
//判断是否左边窗口需要缩减,如果已经包含,那就需要缩减
while(windows.contains(c)){
windows.remove(s.charAt(left));
left++;
}
windows.add(c);
//比较更新答案
res = Math.max(res,windows.size());
}
return res;
}
leetcode案例分析
我们再来看一道leetcode真题,加深一下印象哈。
题目:给你一个字符串S、一个字符串T。返回S中涵盖T所有字符的最小子串。如果S中不存在涵盖T所有字符的子串,则返回空字符串 "" 。
实例1:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
实例2:
输入:s = "a", t = "a"
输出:"a"
我们还是套用这个框架流程:
- 首先呢,就是获取原字符串的长度。
- 接着维护一个窗口(数组、哈希、队列)
- 窗口一步一步向右扩展
- 窗口在向右扩展滑动过程,需要判断左边是否需要缩减
- 最后比较更新答案
获取原字符串的长度。
这个比较简单,因为原题还是需要有左右指针去遍历字符串S的。
int len = S.length();
接着维护一个窗口(数组、哈希、队列)、右移、左边缩减
我们可以先定义一个最小的窗口,长度为0。定义窗口时,我们得想下:窗口什么时候右移,什么时候左边缩减,怎么比较更新答案。
最小的窗口什么时候可以右移呢?因为题目要求涵盖T的所有子串,所以,窗口一开始就可以右移,直到包含T的所有字母
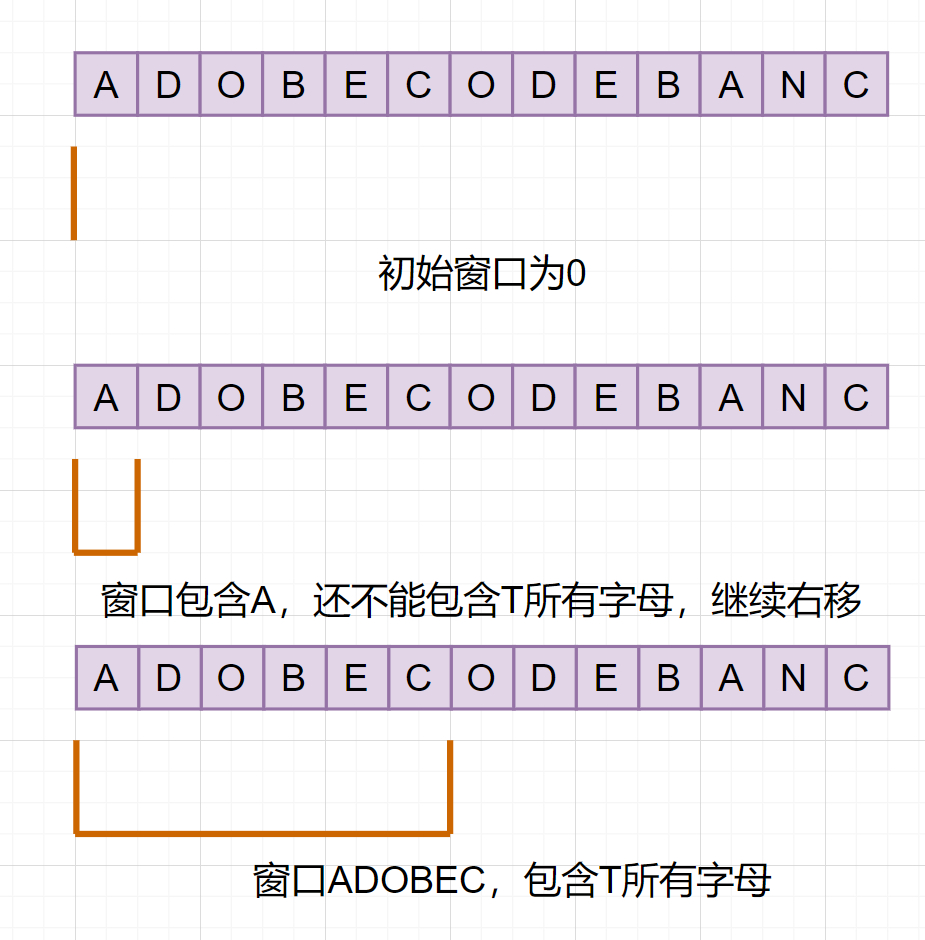
显然,窗口字符串ADOBEC,是S中涵盖T所有字符的第一个子串。但是呢,我们要找的是最小子串,ADOBEC还不一定是最小的。因为:
1.当前窗口可能包含一个满足题目条件的,更小的子窗口字符串。(可以左边缩减) 2.窗口还没滑到的地方,可能包含一个满足条件的,更小的字符串。(可以窗口继续右移)
找到第一个满足条件的窗口字符串ADOBEC后,为了寻找更小的子窗口字符串。我们可以:
1.左边缩减,如果缩小的窗口仍然满足包含T所有字母,那当前窗口就可能是最小子串。存储下来(就类似于滑动窗口框架的更新答案哈),然后继续从左缩减窗口。 2.如果缩小窗口不能满足包含T的所有字母,这时候就可以停止窗口的左边缩减,转而向右扩大窗口啦。
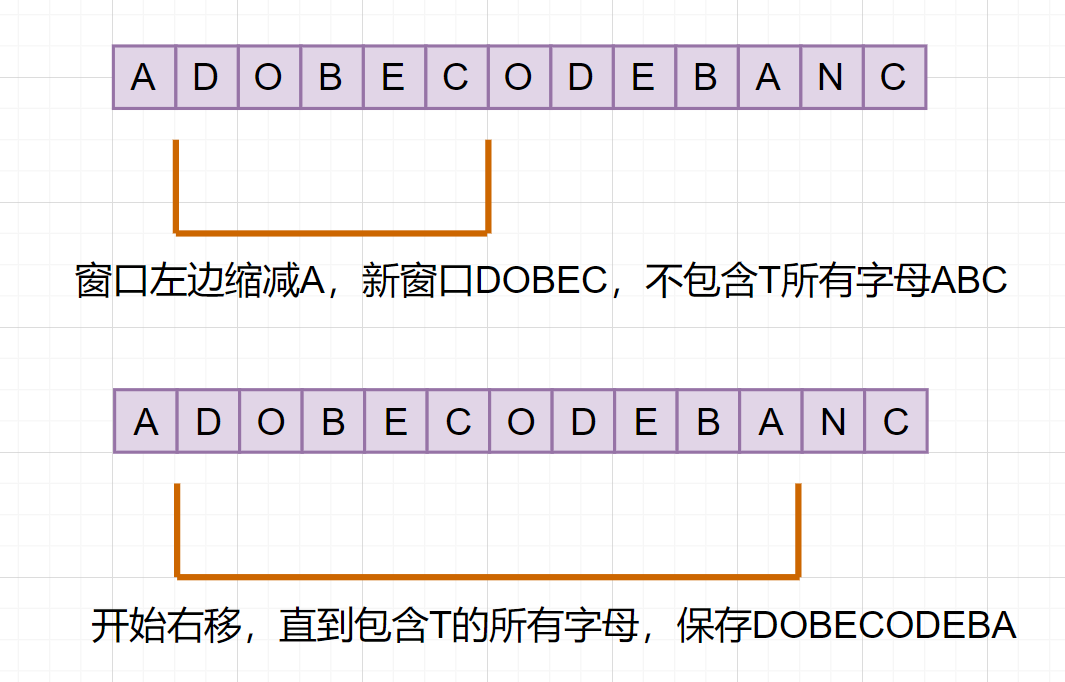
不断重复以上的步骤,把找到满足条件的窗口保存下来,比较得出最小的子串。示例满足条件的最小子串是BANC
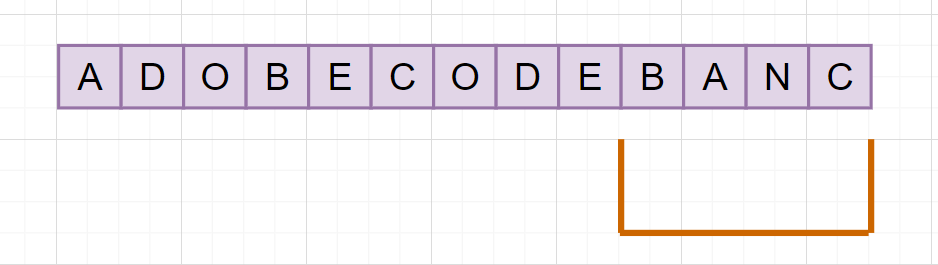
这道题的难点,其实是如何判断S的子串包含T,我们一起来看下代码吧:
class Solution {
public String minWindow(String s, String t) {
if (s.length() == 0 || s.length() < t.length()) {
return "";
}
int sLen = s.length();
Map lookup = new HashMap<>();
for (int i = 0; i < sLen; i++) {
lookup.put(s.charAt(i), 0);
}
for (int i = 0; i < t.length(); i++) {
Character c = t.charAt(i);
if (lookup.containsKey(c)) {
lookup.put(c, lookup.get(c) + 1);
} else {
return "";
}
}
int left = 0;
int right = 0;
int minLen = Integer.MAX_VALUE;
int tCount = t.length();
String result = "";
while (right < sLen) {
char c = s.charAt(right);
if (lookup.get(c) > 0) tCount--;
lookup.put(c, lookup.get(c) - 1);
//窗口右移
right++;
//已经包含T的所有字母
while (tCount == 0) {
//比较更新答案
if (minLen > right - left) {
minLen = right - left;
result = s.substring(left, right);
}
char c2 = s.charAt(left);
if (lookup.get(c2) == 0) tCount++;
lookup.put(c2, lookup.get(c2) + 1);
//窗口从左边缩减
left++;
}
}
return result;
}
}
leetcode提交结果如下:
这道题是字节一面真题,大家可以细看一下哈,也可以加我微信(tianluoboy1024),一起讨论一下。
推荐阅读:
欢迎关注微信公众号:互联网全栈架构,收取更多有价值的信息。
