从零开始写一个推荐系统第一篇，谁和你相似-技术圈

1. 谁和你相似

我们在电商网站上购买一件商品后，网站总是会提醒我们，购买这件商品的用户还购买了哪些商品，网站会猜出你可能会购买的商品。网易云音乐有一个每日推荐功能，会根据你的个人喜好为你推荐一批歌曲。这些推荐并不是随机的，而是经过一系列复杂的计算生成的。

网站背后的算法是非常复杂的，但可以总结为一个简单的目标：找到和你相似的人，把这个人喜欢的东西推荐给你。

那么谁和你相似呢？这又是一个复杂的问题，为了找到和你相似的人，必须将人的行为进行量化，所谓量化，就是用数学来描述人的行为。假设有4部电影，分别是霸王别姬，雷神，大话西游，战狼。你，小明，小红三个人对这4部电影的评分如下

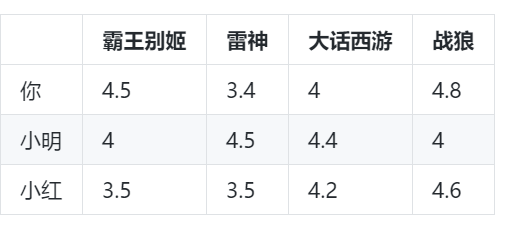
想要找到和你观影品味相似的人，需要对你们的行为进行量化，所得到的的是一份对电影评分的明细表，这里记录了你们三个人对这4部电影的评分。

接下来，我们需要一种方法，通过这些评分来计算出谁和你最相似。不要想当然的通过人为观察数据来判断，这样做是没有说服力的。

我们有两种算法可以拿来使用：

欧几里得距离
皮尔逊相关度

2. 欧几里得距离

我们从一个简单的例子出发来讲解欧几里得距离是怎么一回事。你，小明，小红三个人是同班同学，这次考试，你们的语文成绩分别是90， 95， 88分，谁和你最相似呢？

小明和的分数相差了5分，而小红和你的分数相差了2分，小红和你最相似。但考试不只考语文，还有数学，分数情况如下

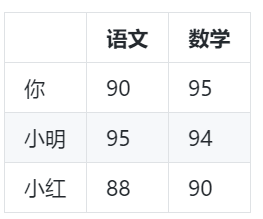
加上数学分数后，谁和你最相似呢？这里不能用总分来描述学习能力的相似，学习能力是由多个科目综合作用的结果，有可能你和某个人的总分是一样的，但是你数学0分，语文100，而他数学100，语文0分，尽管总分一样，但你们的学习能力明显相差巨大。我们可以在直角坐标系里把你们三个人的分数表示出来，语文做x轴，数学做y轴。我用plotly 在jupyter里做了一张图

import plotlyimport plotly.offline as pypy.init_notebook_mode(connected=False)import plotly.graph_objs as go
dataset = {        '语文': [90, 95, 88],        '数学': [95, 94, 90],    }
data_g = []
data = go.Scatter(        x=dataset['语文'],        y=dataset['数学'],        text = ['你(90, 95)', '小明(95, 94)', '小红(88, 90)'],        mode='markers+text',        textposition="top right",        name='考试成绩')
data_g.append(data)
layout = go.Layout(title="考试成绩",                       xaxis={'title': '语文'}, yaxis={'title': '数学'})fig = go.Figure(data=data_g, layout=layout)fig.show()

生成的成绩图如下

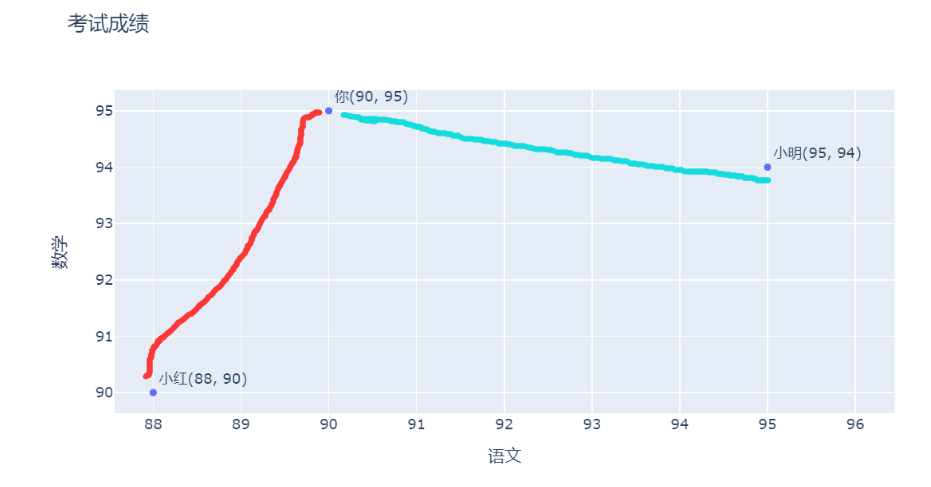
到底是红色线段更短还是青色的线段更短呢？距离越近，说明两个人学习能力越相似。这个问题已经被转换成计算平面内两个点的距离，公式如下

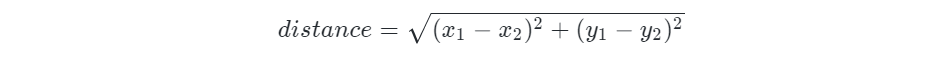
用python计算你和小红的距离

import math
distance = math.sqrt(pow(90 - 88, 2) + pow(95 - 90, 2))print(distance)     # 5.385164807134504

计算你和小明的距离

import math
distance = math.sqrt(pow(90 - 95, 2) + pow(95 - 94, 2))print(distance)     # 5.0990195135927845

显然，你和小明的距离小于小红，小明的学习能力和你更为相似。

除了语文，数学，还会有英语

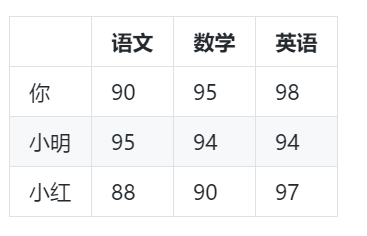
现在有3个科目，3个维度，已经不能在二维平面上把这3个人的数据画出来了，想要画出来，需要x,y,z三个轴，但再增加一个科目呢？不管有多少科目，多个维度，计算他们之间距离的方法是不变的

import math
# 你和小明的距离distance1 = math.sqrt(pow(90 - 95, 2) + pow(95 - 94, 2) + pow(98 - 94, 2))print(distance1)     # 6.48074069840786
# 你和小红的距离distance1 = math.sqrt(pow(90 - 88, 2) + pow(95 - 90, 2) + pow(98 - 97, 2))print(distance1)     # 5.477225575051661

加上英语，小红的学习能力与你更相似。我们在表示相似程度的时候，并不是直接使用欧几里得距离，而是将其与1进行比较，相似度在0和1之间，距离1越近，表示越相似，因此评价相似程度时，要使用公式：

1/(1+distance)

用代码来表示

def sim_distance(lst1, lst2):
    sum_value = 0
    for x1, x2 in zip(lst1, lst2):
        sum_value += pow(x1 - x2, 2)
    return 1/(1 + math.sqrt(sum_value))

3. 皮尔逊相关系数

皮尔逊相关系数，很难像欧几里得距离那样形象的解释，它的算法也更加复杂，涉及到了矩阵，哎，线性代数的内容啊，当年考试就不及格。。。。。。

既然难以解释，就不解释了，直接上数据

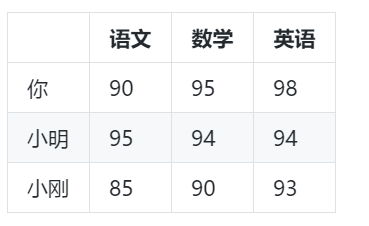
计算你和小明的欧几里得距离是6.48074069840786，和小刚的欧几里得距离是8.660254037844387，似乎小明的学习能力和你更为接近，但是，如果仔细观察数据就能发现，小刚的学习能力其实和你更接近，理由如下：

分数上看，你的英语分 > 数学分 > 语文分，小刚也呈现出相同的规律
小刚各科的分数都比你少5分，你们的数学都比语文多5分，英语都比数学多3分
反观小明，他语文成绩比你好，数学和英语分数相同，而你的英语比数学好，他的各科分数语文分 > 数学分 = 英语分

以上分析，反应出的是两组数据之间的相关性，你和小刚的成绩呈现出比较明显的正相关性，假设化学你考了96分，根据规律大体可以猜测小刚的化学分数是91分，还是差了5分。小刚的成绩与你的成绩就没有呈现出比较明显的正相关性，让你猜测小明的化学分数，你能像猜小刚的化学分数那样肯定么？

皮尔逊相关系数可以衡量两个数据集合是否在一条线上面，计算出来的结果在-1到1之间，负数表示负相关，正数表示正相关，0表示不相关，数值越大，相关性越强。

计算你们3个人之间的皮尔逊相关系数

import math
import numpy as np

lst1 = [90, 95, 98]
lst2 = [95, 94, 94]
lst3 = [85, 90, 93]

def cal_pccs(x, y):
    '''
    皮尔逊相关系数
    '''
    count = len(x)
    sum_xy = np.sum(np.sum(x*y))
    sum_x = np.sum(np.sum(x))
    sum_y = np.sum(np.sum(y))
    sum_x2 = np.sum(np.sum(x*x))
    sum_y2 = np.sum(np.sum(y*y))
    pcc = (count*sum_xy-sum_x*sum_y)/np.sqrt((count*sum_x2-sum_x*sum_x)*(count*sum_y2-sum_y*sum_y))
    return pcc


def sim_distance(lst1, lst2):
    sum_value = 0
    for x1, x2 in zip(lst1, lst2):
        sum_value += pow(x1 - x2, 2)
    return 1/(1 + math.sqrt(sum_value))

print(cal_pccs(np.array(lst1), np.array(lst3)))     # 1.0
print(sim_distance(lst1, lst3))     # 0.10351694645735657

print(cal_pccs(np.array(lst1), np.array(lst2)))     # -0.9285714285714286
print(sim_distance(lst1, lst2))     # 0.13367660240019172

以皮尔逊相关系数做为评价标准，你和小刚的学习能力更为接近。

现在，我们已经掌握了两种度量相似度的算法，下一篇文章，我们将使用一份电影评分数据进行实战训练，指定一个参与评分的用户小A，计算得出和他相似性最高的5个人，并根据这5个人对其他电影的评分为小A推荐几部电影。