几何和代数是怎么走到一起的？-技术圈

数学算法俱乐部

日期： 2021年04月12日

正文共：3140字

来源：《少年时》

当欧氏几何走到了头

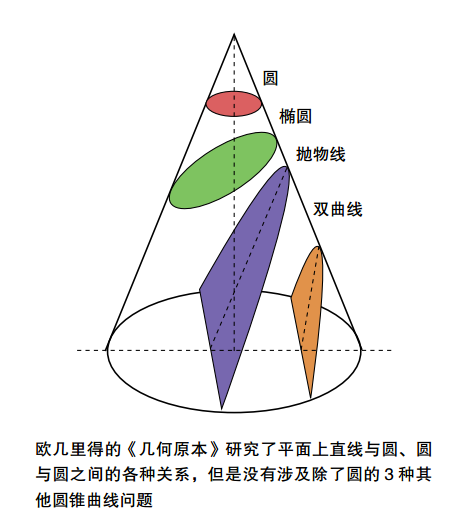
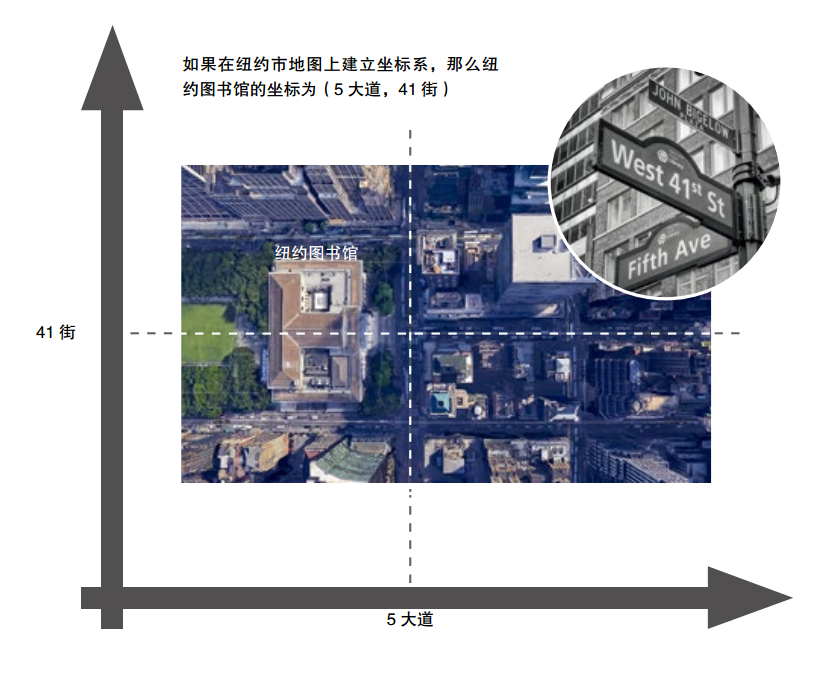
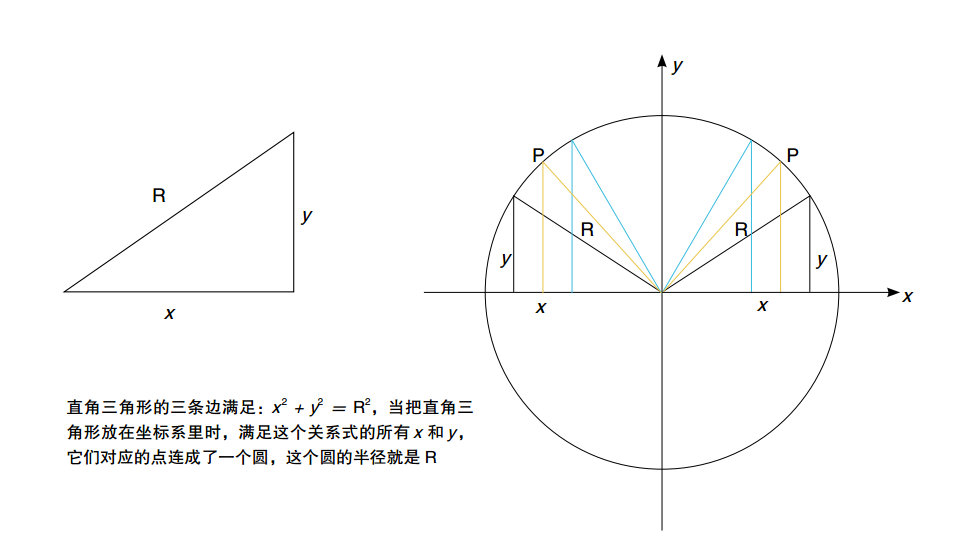
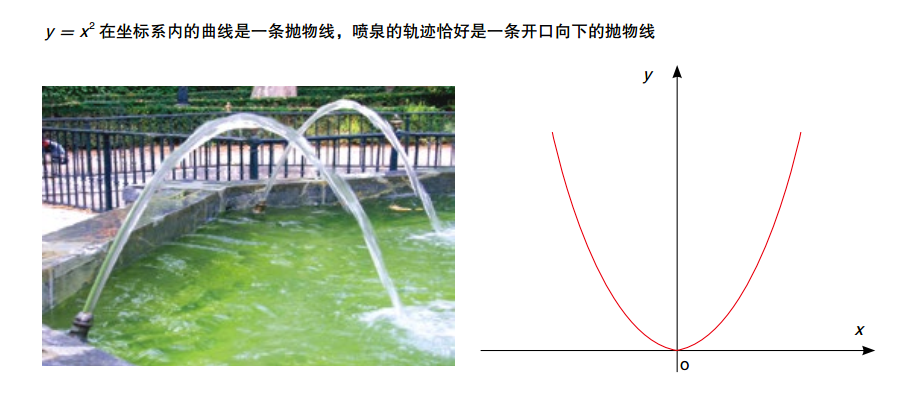
17 世纪早期，尽管科学在各个领域有了重大突破，但是数学还只有一个几何体系，就是根据古希腊数学家欧几里得所著的《几何原本》创立的经典平面几何体系。这个体系仅适用于由直线和圆组成的图形。这时候的代数，不过是几何的附属品。

然而，随着人们对科学的不断深入探索，许多新的奇形怪状的图形相继出现，这些都没有办法通过欧氏几何理论进行分析。比如，为了描述天体运行的轨道，天文学家绘制了椭圆、双曲线、抛物线，其中抛物线也很好地勾勒出炮弹出膛后的运动轨迹；在海上航行时人们常常借助月亮来判定方位，因此人们迫切需要了解月球的运行轨迹和规律；望远镜和显微镜的发明，使透镜走进了人们的视野，但是人们对透镜的性质和参数却完全没有概念，比如说透镜表面应该是做成什么样，才能有最好的光线会聚性能？

要解决这些问题，需要了解曲线的概念和定量分析方法。但是欧几里得没有提出任何有关曲线问题的解决方法，古希腊人在圆锥曲线（平面与圆锥体相交得到的曲线）方面留下的著述也非常少。没有可以参考的方法，这是当时的数学家所面临的困境，数学方法的落后甚至妨碍到了整个科学的发展。

这时，有一位法国数学家率先站了出来，明确地表示了对欧氏几何那套方法的强烈不满。欧几里得的《几何原本》里提到的每一个问题，证明过程都需要一个新颖、奇巧的方法，不但过于抽象，而且多依赖于图形，甚至需要解题者具有非凡的想象力。古希腊数学家虽然在研究数学问题上花费了大量的时间，却从不考虑它们的实际应用问题。他直接抨击欧氏几何“成了一门充满混乱和晦涩、有意用来阻碍思想的记忆，而不是一门有益于思想发展的艺术”。

这位数学家，就勒内• 笛卡尔（René Descartes）。

1637 年，他发表了著作《方法论》。在一篇叫作《几何学》的附录中，他提出了一种不依赖于图形也更为普遍的方法，这就是将代数应用于几何，把几何和代数中的精华部分结合起来，互相以长补短，我们称之为“解析几何”。

数学的“魔钥匙”

1596 年，笛卡尔出生于法国拉艾的一个中产阶级家庭。8 岁那年，他数学产生了兴趣，在接受了 10 年的正规学校教育之后，他决心通过直接的身体验来更好地了解世界。他到巴黎体会了浮华的生活，又回到了拉艾进行了一段时期的沉思。后来，他时而随军参战，时而四处旅行，时而在巴黎醉生梦死。最后，他决心安定下来。在接下的 20 年里，他大部分的时间和精力都用来著述。

在笛卡尔活跃的一生中，他其实一直在思考，“我们怎么理解事物，如何才能获得真理？”尽管真理不会自己产生，但是对笛卡尔来说似乎有些例外。至少他自己是这样说的，他的灵感来源于一个梦境。

1619 年 11 月 10 日，在庆祝圣马丁节的盛宴上狂饮之后，笛卡尔做了一个生动的梦。据笛卡尔所说，“在梦中他正用不带迷信的科学眼光，观察着凶猛的风暴，他发现一旦他看出风暴是怎么回事儿，它就不能伤害他了。”这个梦境仿佛向他展示了一把“魔钥匙”，这把钥匙能打开大自然的宝库，并使他掌握所有科学的真正基础。尽管，笛卡尔并没有明确说明这把神奇的钥匙是什么，不过人们通常认为这就是把代数应用于几何的方法，就是解析几何。

他认为，代数可以很好地弥补几何在抽象方面的不足，因为代数可以直接用抽象的符号和数字进行推理，而且代数还可以把推理过程变得程式化，从而让每一个人在面对数学问题时，不必因为想象力的限制而裹足不前。

于是，一种新的数学方法应运而生，这就是现在众所周知的解析几何，也是现代应用数学的基础。

人们把 1619 年 11 月 10 日当成解析几何诞生的日子，也是现代数学的诞生日。解析几何理论就像一道光一样，将蒙在数学家眼前的黑暗渐渐驱散，迎来了数学界的崭新的黎明。

公式和图形牵手

解析几何因为它的简单而格外引人注目。就像数学中所有真正伟大的东西一样，解析几何的基本概念简单到近乎一目了然的地步。这个基本概念就是坐标系。

几何中最简单的图形是直线，直线很容易理解，也很容易描述，笛卡尔就想办法用直线来表示曲线。在平面上放置两条相互垂直的直线，以相交的位置作为原点，指定这两条直线的方向，画上刻度，就建立起了笛卡尔平面直角坐标系。对于坐标系内的某一个点，我们可以用一对数字来表示（x，y），用正负号表示它具体位于原点的哪一侧，x 和y 分别表示它在两个方向上离开原点的距离。这对数字，我们称为“坐标”。

比如，一座城市的地图上，大道从南到北按数字分成 1 大道、2 大道、3道……街由东向西按数字分成 1 街、2街、3 街……我们可以把大道和街建成一个坐标系，任何建筑都可以按照靠近哪个大街—大道交口来定位。比如纽约图书馆的位置位于：5 大道和 41 街的交口。

通过构建坐标系，几何图形或者说曲线上的任何点，都可以用两个数来表达了。原本复杂的几何问题就转化成了能用公式和数字来表达的代数问题，接下来需要做的就是按照代数方法来计算。我们来看一个典型的例子。

勾股定理说直角三角形两直角边的平方和等于斜边的平方。如果我们把这个直角三角形放到坐标系里，让一个锐角顶点位于原点，锐角相邻的直角边与x 轴重合。

我们把三角形的斜边长设为R，两直角边分别为 x 和 y，那么对应于 R，我们可以画出不同的x、 y 组成的很多个三角形，它们都满足关系式：

x²+ y²＝ R²，

当我们把这些三角形的另一个锐角的顶点连起来时，就得到了一个圆，而这个圆的半径就是 R。

于是，我们就在代数方程和几何图形之间建立起了联系。这就是笛卡尔建立的解析几何体系，按照这种思想，任何几何曲线都可以通过建立坐标系用一个方程来表示。反过来，对于一个已有的方程，数学家也可以在坐标系内画出它的样子，一根曲线、一个曲面，或者是一个球面，从而进一步研究它的性质。比如：

y ＝ x²，

通过在坐标系里描点、连线，我们可以得到这个方程对应的曲线，这是一根抛物线。抛物线在科学、技术、工程等领域中广泛出现。

2 000 多年前，古希腊数学家在研究圆锥曲线时已经发现了抛物线，但只有到了解析几何，才能对抛物线进行有实用价值的定量研究。

更重要的是，笛卡尔的解析几何并不限于平面几何，而是同样适用于三维甚至多维空间。在三维空间内，我们可以在平面坐标轴的垂直方向上增加一条“z”轴，并用 3 组数（x，y，z）来代表空间内的每一个点。比如，我们在绘制三维城市地图时，只需在考虑建筑物位于大道和大街的位置之余，增加一个表示建筑物高度的参数。

在坐标系上建筑现代数学

为了构建一种更好的数学方法，笛卡尔把方程和曲线结合了起来，也把代数和几何合二为一，让代数不再附庸于几何。坐标系的应用不仅把几何上已有的曲线转化成了方程，也通过构建方程定义了一些复杂的曲线，大大简化了复杂曲线的分析过程。虽然曲线千变万化，构建方程的方法却始终如一。

在建立了坐标系后，平面上的一曲线可以通过两个变量的函数方程来表示，这不仅把代数和几何联系起来，而且还把变量、函数等重要概念密切联系了起来，由此也对牛顿的研究有了一定的启发。在牛顿发表的《流数法与无穷级数》中，采用了很多解析几何的方法，而牛顿的流数法正是我们现在所说的微积分。

尽管笛卡尔的解析几何主要解决的是圆锥曲线的问题，但在他的理论基础上，17、18 世纪的科学家还引入了一些其他的新坐标系，解决了一些更为复杂的曲线问题。在那个科技文明大发展的时代，解析几何的思想解决了天文学、力学和技术中的许多实际问题。笛卡尔的工作大大提高了数学在科学研究中的地位，也向全世界证明了数学在探索真理过程中发挥的作用和力量。解析几何的提出，是一个时代结束的标志，为日后微积分的出现奠定了坚实的基础，而后者又是现代数学的基石。

— THE END —