Sampling-Argmax：用重参数技巧优化Soft-Argmax

本文是ICCV2021 Oral论文RLE作者在NeurlPS2021上的文章，经知乎上一个小伙伴推荐给我，读后感觉大有收获，这篇文章我非常喜欢，并且可以预见地能广泛应用于目标检测、姿态估计等各种关键点定位的任务中，于是赶紧写了这篇笔记来跟大家分享一下~

论文地址：

https://jeffli.site/sampling-argmax/resources/neurips2021-sampling-argmax.pdf

开源地址：

https://github.com/Jeff-sjtu/sampling-argmax

另外，在实验了RLE+TokenPose+SimDR涨点显著后（实验结果见SimDR文章），我意识到本文的技巧可以替换到SimDR上，之后我也会做实验验证（挖坑待填），结果出来后会在本文下面更新。

由于考虑到没有相关前置知识的小伙伴，本文我写得尽量通俗易懂，可能显得有点啰嗦，希望水平较高的小伙伴见谅~

根据我起的文章标题，也许你会产生以下几个疑问：

1. Soft-Argmax是什么？
2. Soft-Argmax为什么效果好？
3. Soft-Argmax有什么问题？
4. 前人难道就没有意识到Soft-Argmax的问题吗？
5. 重参数技巧是什么？
6. 为什么要用重参数技巧？

请带着这些疑问进行本文的阅读。

0. 前言

在关键点定位任务上，天下苦Heatmap-based方法久矣，我也写了很多篇文章来列举Heatmap-based方法的弊端，以及近年来超越它的方法，在这里就不一一进行赘述了，感兴趣的小伙伴可以阅读我RLE的笔记文章前言部分，在那一篇中我对Regression-based方法和Heatmap-based方法进行了最详尽的介绍。

简单来说，关键点定位任务，从模型预测结果的角度来看可以分为两个流派：直接预测坐标值和预测关键点的概率分布图。

预测坐标值很好理解，模型输出的结果就是坐标数值；而预测关键点概率图的方法，每一个关键点对应了一张概率图，我们取图上概率最高的点作为模型的预测结果，而这里获取最大的那个item的index的操作，称为Argmax。

不难发现，Argmax操作是不可微的，因此在模型训练时，梯度无法传递过Argmax，因此在预测概率分布图的方法中，我们无法直接对坐标值进行监督。更糟糕的是，Argmax还会承受量化误差，因为它获取的是概率图上像素点的坐标，我们不得不要求概率图的尺寸越大越好，这又增加了许多计算量。

后来大家想出了Soft-Argmax操作，对于一维离散概率图 ，每一位的取值为 ，Soft-Argmax公式如下：

即对模型输出的概率图进行Softmax后，逐像素乘上坐标[0 1 2 3 ... n]，这样可以近似地获得跟Argmax近似的结果，且梯度可以回传，还使得输出特征图不再受到尺寸限制。在姿态估计领域，这就是DSNT和Integral Pose两篇文章的来源了。

对于DSNT的深度分析我推荐@深度眸大佬的这篇文章：https://zhuanlan.zhihu.com/p/53057942。

Soft-Argmax为什么效果好？

我们都知道在有监督训练中，人工标注了关键点位置，模型进行拟合。

这个过程的潜台词是：

人工标注的点都是正确的，我们只要用模型尽量逼近标注点就好了。

但是人就会犯错误，我们的标注是有误差的，人工标注的结果应该是围绕着真实位置，以某种概率进行分布的。而在自然界中，这种分布一般都可以看成是高斯分布，也就是我们熟悉的那个正态分布的形状。

Soft-Argmax其实相当于对人工标注进行了一次软化，让我们的人工标注不那么强硬和自信，从学习one-hot变成了学习一种概率分布，这种思想在分类任务中早有用到，也就是LabelSmoothing。

Soft-Argmax的问题

有了Soft-Argmax后，大家可以快乐地直接对坐标值进行监督了，模型还能预测概率图，性能强过单纯用全连接层回归坐标值，大家都很开心，但是大家很快发现，这种方法比起Heatmap-based方法依然有很大差距，尤其是在大尺寸输入的情况下，Heatmap-based方法摆脱了量化误差束缚，性能甩了坐标值监督方法几条街，Soft-Argmax只能在小尺寸、低算力设备上占占便宜。

要分析Soft-Argmax方法的问题所在，其实很容易发现，假如把输出看成离散概率分布的话，它计算的是概率分布的期望，当我们对坐标值直接进行监督时，关注的也只是期望值，而对概率分布的形状是无约束的，换句话说，一个期望值可以对应无数种可能的分布形状，这对网络学习显然是有害的。

在李翔老师的论文GFLv2中也对该问题进行过深度分析。在GFLv1他中提出了用一维概率分布来建模目标检测边界框的位置，用求期望的方式得到坐标值，这其实就是用的Soft-Argmax。

而在GFLv2中，通过统计的方法，他发现概率分布的形状与结果的质量是高度相关的：

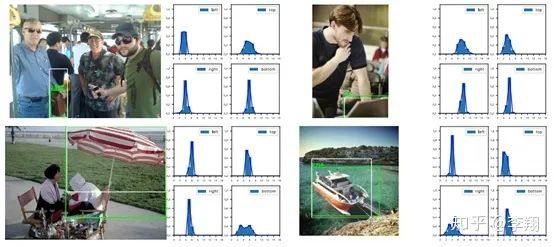
大家可以看到，基本上那些非常清晰明确的边界，它的分布都很尖锐；而模糊定义不清的边界（如背包的上沿和伞的下沿到底在哪里傻傻分不清）它们学习到的分布基本上会平下来，而且有的时候还经常出现双峰的情况。

一个“好”的概率分布形状，应当是“单峰且尖锐的”，换句话说，概率分布最高值点应当正好在GroundTruth附近。而“不好”的概率分布形状各异，根据这个形状我们就可以判断模型对于自己输出的“自信程度”，用专业术语来讲是不确定度（uncertainty）。如果目标的定位边界都不那么准确，你的分类结果是不是也不应该那么自信呢？GFLv2由此学习出一个自适应的权重来指导模型的分类表征，是非常高效且合理的。

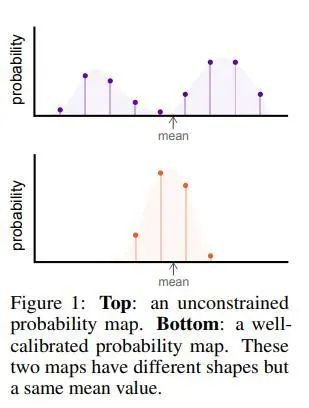
在明确了“好”的形状是什么样后，很自然地我们就会想，怎么样才能让模型去学习“好”的概率分布形状呢？即，如何对概率分布的形状进行约束？

至此，我们将正式进入本文的核心部分~

1. 方法

人工设计约束

概率分布形状的问题很早就被意识到了，大家也想到了要对其进行约束，早在DSNT工作中，作者就提出了加入正则项来约束形状，并想出了两种正则方式：方差正则和分布正则。

方差正则就是控制输出概率图的方差，要求它逼近目标的方差，可以写成：

分布正则就更简单直接了，既然你希望得到高斯热图，那我就求输出概率图毕竟目标高斯热图，这不就是Heatmap-based方法的精髓嘛。DSNT作者还通过实验对比了计算KL散度和JS散度哪个性能更好，最终选择了计算概率图与目标二元高斯分布的JS散度作为正则项：

但是，这种人工预设的概率分布，跟真实数据分布之间，是存在差异的，在有的情况下甚至可能产生副作用降低模型性能（本文后面有实验证明这一点）。那么，有没有可能让模型学习数据的真实分布呢？

初步尝试

如何对概率分布的形状进行约束呢？本文提出将优化的目标，从最小化“期望的误差”（the error of the expectation）变成最小化“误差的期望”（the expectation of the error）即可。

在过去的传统做法中，我们都是先对概率分布求期望，再计算期望与GroundTruth的距离损失，公式可以写成：

而误差的期望则是改变顺序，先计算误差，再对误差求期望：

这种近似方式，是将target位置看成一个离散分布，即每个像素点对应了一个概率

但这种方法是有问题的，由于真实的target分布是在连续空间上的，受限于概率图的分辨率，用离散分布来建模是有误差的。

用上面的目标函数在COCO Keypoint数据集上做实验，发现模型收敛非常慢，最终性能也很差，只能取得30.9mAP，而过去用Soft-Argmax方法训练的模型都能取得64.5mAP。

作者分析了这种离散近似方法下的损失函数梯度：

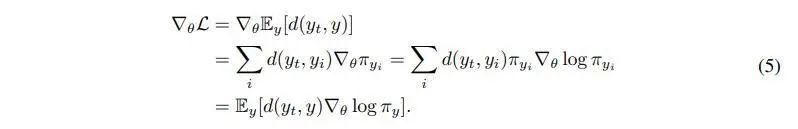
发现这个形式与SF估计（Score function Estimator）非常相似，而SF在VAE的原始论文“Auto-Encoding Variational Bayes”里已经指出其方差很大，这里我找了一下SF的梯度公式：

关于SF估计方差大的弊端，苏剑林大佬举过一个例子：

什么是方差很大？它有什么影响？举个简单的例子，假如α=avg([4,5,6])=avg([0,5,10])，也就是说，我们的目标α是三个数的平均值，这三个数要不就是4,5,6，要不就是0,5,10，在精确估计的情况下，两者是等价的，但是如果每一组只能随机选其中一个数呢？第一组可能选到4，这也没什么，跟准确值5只差一点；但是第二组可能选到0，这跟准确值5差得就有点大了。也就是说，随机选一个的情况下，第二组估计的波动（方差）太大了。类似地，SF估计出来的梯度方差也是如此，这导致了我们用梯度下降优化的时候相当不稳定，非常容易崩。

初步尝试陷入了困境，相信这种思路绝对不是第一次被人想到，但是大家都卡在了这里。

重参数技巧

直接使用“误差的期望”的离散近似形式，作为目标函数来训练的思路行不通，于是作者想到了重参数技巧（Reparameterization trick）。

关于重参技巧和Gumbel-Softmax相关的资料很多，在这里我推荐苏剑林大佬的《漫谈重参数：从正态分布到Gumbel Softmax：https://link.zhihu.com/?target=https%3A//spaces.ac.cn/archives/6705这篇文章，感兴趣的小伙伴可以去阅读一下。

下面我简单地进行一下介绍：

重参数是处理如下期望形式的目标函数的一种技巧：

其数学本质是一种积分变换，目前我们常用的一种重参技巧是Gumbel-SoftMax，能通过采样的方式来得到以上目标函数的有效估计。

这个技巧在VAE、文本GAN、强化学习中都有用到，根据z的连续性，又可以分为连续形式和离散形式。该技巧可以帮助我们最小化 的同时，还能更新参数 。

有没有发现，这正是我们“误差的期望”的公式。因此我们找到了另一条路，从 中采样，并且保留 的梯度，最关键的是，该方法的梯度形式不存在SF估计那样的严重问题。

连续混合分布

有了重参数技巧的前置知识后，一切瞬间豁然开朗了起来。

重参技巧是怎么做的呢？基于 进行采样，在优化目标函数的同时更新模型参数。因此我们可以用采样的方法来估计误差的期望。

要使用采样方法来估计期望，我们除了需要一个可微分的过程以外，还面临的一个更麻烦的问题：随着输入图片的变化，目标的概率密度函数是会改变的。

这个问题不难理解，由于图片内容不同，关键点的概率分布密度函数应当是不一样的，这也是为什么人工指定的概率分布约束存在局限性。

本文将目标概率分布视为连续空间上的混合分布，对问题进行了深入分析。

那么混合分布又是啥？

引用sola大佬对混合分布进行一下简单介绍：

混合分布是一个很有趣的概念。它被定义的出发点是为了解决这样一个问题：已知X1，X2这两个随机变量的概率分布，现有随机变量Y，Y有概率p具有和X1同样的分布，有概率1-p具有和X2同样的分布，那么对于这样的随机变量Y，其密度为X1，X2的密度的加权平均，权重为p和1-p，我们称Y为X1，X2以权重p，1-p生成的混合分布随机变量。

详细的介绍请看这篇文章：https://zhuanlan.zhihu.com/p/45954178，这里我们只需要知道混合分布具有以下性质：

密度函数

期望

即，混合分布的目标密度函数等于子密度函数的加权和：

而回到我们的实际场景中，我们可以把目标密度函数看成是把一块[0，W]的区间分割成了n块，如下图（a）所示：

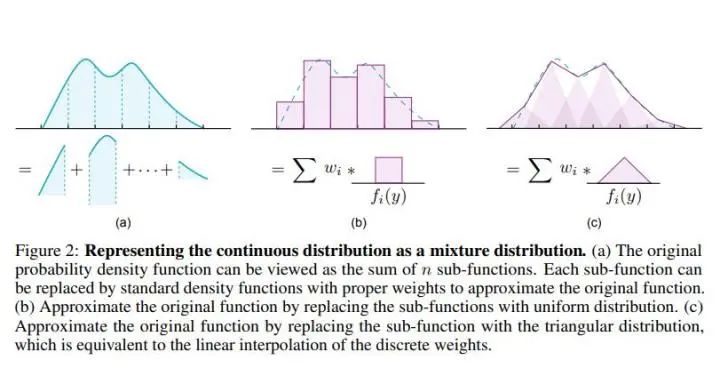
我们可以用不同形状的子密度函数来构成整个目标密度函数，常见的形状有矩形、三角形、高斯函数等。

因此，我们可以利用模型输出的概率图 中，每个位置上的概率值 来代表权重 ，这个权重的作用是对标准形状进行拉伸和压扁。

但是我们的目标概率分布是在连续空间上的，而我们的图片是离散的，根据香农采样定理，采样率必须要达到目标频率的两倍，目标函数才能被完美重建，这对于我们的情况来说是不现实的，我们只能退而求其次追求一个近似的结果。

本文根据常见形状，设计了三个标准密度函数：

均匀分布（矩形）：

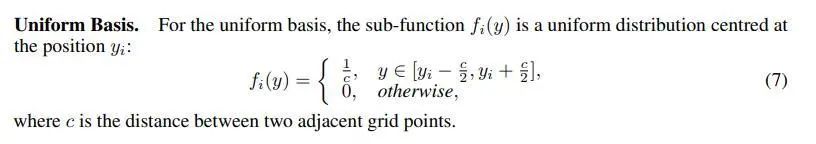
三角分布（三角形）：

高斯分布（我们熟悉那个形）：

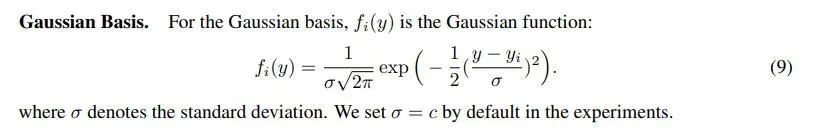
这一步告诉了我们如何生成标准形状，而我们的目标密度函数，所谓的加权和，可以看成是在不同位置上，根据权重把标准形状进行了拉伸或压扁，也就是图中的（b）和（c）了。

不可微分采样

说完了概率密度函数的问题，现在需要讲一下采样了。

要从一个混合分布中取样本，作者先从不可微分的采样过程入手进行分析。

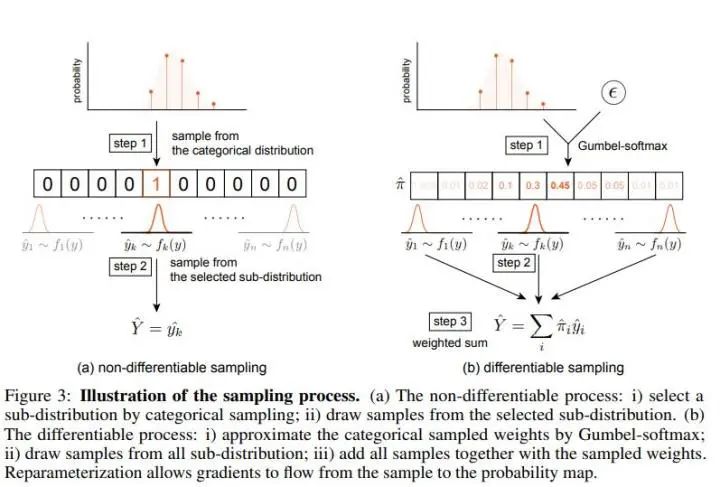
由于混合分布的定义我们知道，Y有p的概率跟X1同分布，因此不可微分的采样过程可以拆分为两个步骤：

1. 确定样本来自于哪个子分布
2. 从该子分布中取样

在第一步中，由于一个样本只会来自一个子分布，因此是one-hot的，这个确定的过程可以看成是从类别分布（Categorical Distribution）中随机取样，而取样概率为模型预测的概率图 。换句话说，就是用模型预测的概率图来生成one-hot向量，假如我们生成的向量数目足够多，这些向量相加取平均便能得到原始的概率图。

我画了一个图来说明这个过程：

在不可微分采样过程中，我们一般采用Gumbel-Max技巧来得到这样的类别分布。

第二步就很容易实现了，跟输出概率图无关，因此让本过程变得可微的核心在于，让第一步变得可微。

而如何从子分布中取样呢？根据上面三种标准密度函数的生成公式，我们可以生成在每一个像素位置上对应形状的分布向量，它们是固定的。在不可微过程中采样是one-hot的，因此只需要取对应的那一个标准形状的向量即可。

可微分采样

不可微分过程是我们设计可微分过程的基础，指导了我们前进的思路，可微分采样过程有三个步骤：

1. 用Gumbel-Softmax来获得类别权重
2. 从子分布取样
3. 取样多次，计算加权和

虽然比不可微过程多了一个步骤，但是实际上还是两步，第二三步实际上共同对应了不可微中的第二步。

由于Gumbel-Max技巧是不可微的，因此我们需要用到Gumbel-Softmax，顾名思义，是对Gumbel-Max的光滑化，使其可以微分。该技巧被广泛地应用于各种基于采样的训练中。

在第一步中，由于Gumbel-Softmax得到的不再是one-hot的类别分布了，由于进行了光滑化，所以只是形状近似于one-hot的概率分布（可以类比Max和Softmax的结果来理解），随着温度系数 的改变，系数越趋近于0时，得到的结果越逼近one-hot。因此我们说Gumbel-Softmax得到的是类别权重（Categorical weights），我们可以将其视为对不同子分布的采样权重。

以下是Gumbel-Softmax得到的采样结果公式， 对应了在每一个子分布 上的采样权重：

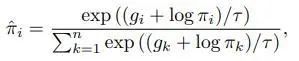
在第二步中，由于我们得到的不再是one-hot的，而是一条形似one-hot的权重概率。换句话说，one-hot相当于指定了从某一个子分布100%采样，而Gumble-Softmax的结果是按权重对每个子分布采样，最后合起来：

我也画了一张图来形象化说明这一过程：

至此，我们再一次得到了期望值，我们将这种采样计算误差期望的过程记作

这种方式的梯度为：

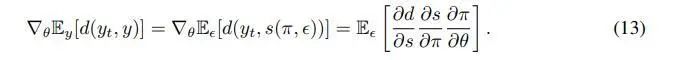
相对于一开始形似SF估计的梯度公式，这种方式的方差就小多了，具体原因也可以前往苏神的博文阅读。

到了第三步，由于Gumbel-Softmax的随机性，我们每次得到的类别权重实际上是会变化的，可以理解为对于同一组数据，Gumbel-Softmax输出的结果并不相同，这也是Gumbel-Softmax跟Softmax的不同之处。

因此，我们还需要多次采样取平均，以保证结果的准确性：

此处 代表了样本个数，或者说调用Gumbel-Softmax的次数。

在使用Gumbel-Softmax训练神经网络的时候还有一个问题需要注意，就是温度系数 的调节。当系数较大时，样本 并不服从原始的混合分布 ，而当系数很小趋近于0的时候，梯度的方差又会逐渐变大，所以训练过程中需要对系数进行调节。

在本文的实验中，我们从一个比较大的温度系数开始，随着训练的进行逐渐缩小温度系数。

由于本文的代码尚未开源，我试着写了一下代码，希望可以帮助大家理解：

# 以一维分布为例，可以直接用在SimDR中，当然也可以推广到二维
featuremap = net(x)

# prepare standard density function
# length等于featuremap的长度
# gen_triangular_basis即生成标准分布的公式
std_basis = [gen_triangular_basis(i) for i in length] 

def categorical_weights(featuremap):
    return F.gumbel_softmax(featuremap, tau=temperature)

loss = 0.
for k in range(N_s):
    cat_w = categorical_weights(featuremap)
    for i in range(length):
        Y_hat = std_basis[i] * cat_w 
        loss = loss + loss_func(Y_target, Y_hat)
loss = loss / N_s

2. 实验

由于Soft-Argmax方法应用应用广泛，本文分别在2D人体姿态估计、3D人体姿态估计、医学图像分割、点云关键点估计上与传统方法进行了对比，这里我主要关注人体姿态估计任务上的表现。

2D人体姿态估计

首先是2D人体姿态估计，本文对Soft-Argmax、加方差正则、加分布正则、以及本文设计的三种标准子密度函数分别进行了实验：

基于三角分布的Sampling-Argmax相较于纯Soft-Argmax有了5.8mAP的提升，另外两种密度函数也表现不错。而且值得注意的是，加正则项的两个实验反而导致了性能下降。

样本个数

由于涉及到多次取样后平均，本文也对样本个数进行了实验探索：

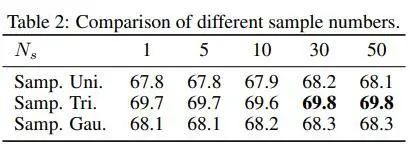
有意思的是，在2D任务上，每次只取一个样本就能得到非常不错的结果，增加样本虽然也能带来提升，但是非常有限。因此在2D任务上，采用较小的样本数是比较经济实惠的。

预测最大值点跟GroundTruth的相关性

在GFLv2中分析到，对于清晰的结果，概率分布的最大值点跟GT是非常相关的，于是本文也进行了验证：

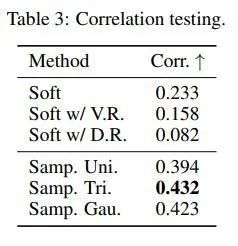
可以看到，相对于Soft-Argmax而言，本文提出的方法大大提升了相关性，其中三角分布带来的提升接近85%，这证明了该方法确实能对分布的性质进行约束，让模型学到更“好”的分布形状。

3D人体姿态估计

在3D人体姿态估计任务上我们可以看到，加方差正则能给模型带来收益，而分布正则导致了性能下降，而本文提出的三种分布则都可以带来更好的提升：

其他更多的实验结果有兴趣的小伙伴请自行参考原文啦。

3. 讨论

在文章的最后，作者发出了这样的感慨：

Although the variants of soft-argmax can bring improvements in some cases, they need laborious tuning of parameters.
In our experiment, we tune the loss weight ranging from 0.1 to 10 and the variance ranging from 1 to 5 for each task. After laborious tuning, the performances of these variants are still not consistent across different tasks and they are inferior to the performance of our method.

这一段辛酸的调参经历属实把我看笑了，字里行间可以看出他们当时在Soft-Argmax实验上应该是花了不少力气调参的，力求取得一个比较强的baseline，但一个实验上的最优参数在另一个任务上还不能通用，于是又是一番辛苦调参hhhh

至此就是本篇笔记的全部内容了，由于笔者数学功底不好，阅读过程中恶补了不少新知识，所写的内容也肯定存在不严谨的地方，欢迎大家批评指正和交流。

能读到这里，说明你是优质读者了，欢迎点一个赞给我鼓励和支持~

感谢相伴。

参考文章：

1. 漫谈重参数：从正态分布到Gumbel Softmax - 科学空间|Scientific Spaces
2. 概率论学习笔记（六） - 知乎 (zhihu.com)
3. 大白话 Generalized Focal Loss V2 - 知乎 (zhihu.com)
4. Numerical Coordinate Regression=高斯热图 VS 坐标回归 - 知乎 (zhihu.com)
5. 碎片化学习之数学（二）：Categorical Distribution - 知乎 (zhihu.com)
6. RLE重铸回归方法的荣光后，回归和热图的异同究竟在何方？| 姿态估计ICCV2021 读后实验 - 知乎 (zhihu.com)

公众号后台回复“数据集”获取30+深度学习数据集下载～