如果我是数学老师,有学生问出这个问题,我肯定非常激动!
日期:2020年08月12日
正文共:2722字2图
预计阅读时间:7分钟
作者:匡世珉
问题:能不能定义一个数I,与 0 的乘积等于 1?
回答分为两部分:第一部分是分析如果定义一个『与0的乘积等于1』的数会导致怎样的后果(实数毁灭);第二部分是解释虚数单位
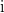 是怎么出现的(使用『模法』)。
是怎么出现的(使用『模法』)。第一部分开始了呦
首先,对于问题的回答是:你当然可以定义一个『与0的乘积等于1』的数,但是这样会使得所有的实数都等于零,于是我们什么有趣的事情都干不了啦。
我们先来想一个问题:大家都知道
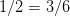 ,可是它们为什么相等呢?
,可是它们为什么相等呢?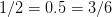 啊!
啊!这不是一个好答案,因为根据小数点的定义,
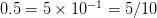 ,所以我们就需要进一步解释为什么
,所以我们就需要进一步解释为什么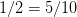 以及为什么
以及为什么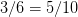 ,于是问题变得更复杂了。
,于是问题变得更复杂了。正确答案是:因为
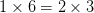 ,所以
,所以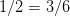 .
.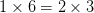 就意味着
就意味着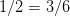 ?
?因为我们就是这么定义两个分数相等的。
不妨先想一想分数到底是怎么回事:
一开始我们只有整数,然后我们把所有非零的整数召集起来,对它们说:『你们也可以当分母哟!』于是,我们就有了诸如
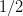 和
和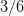 这样的分数。然而这个时候我们并没有对这些分数进行任何限制——没人说
这样的分数。然而这个时候我们并没有对这些分数进行任何限制——没人说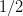 和
和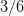 就一定相等。
就一定相等。但是光创造数没有用,我们想做运算呀。现在什么规定都没有,那
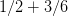 是啥??
是啥??于是人们规定,对于两个分数
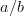 和
和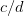 ,如果
,如果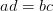 ,那么它们就相等。接着我们就可以定义分数的加法:分母相同的两个分数相加,分母不变,把分子加起来就好了!
,那么它们就相等。接着我们就可以定义分数的加法:分母相同的两个分数相加,分母不变,把分子加起来就好了!这样一来,我们就有了可以做运算的分数(有理数)。更重要的是,当我们把原来的每个整数
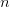 都当成
都当成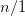 时,有理数的运算和整数的运算是一致的。
时,有理数的运算和整数的运算是一致的。这一点很重要。通常情况下,当我们说『整数集合包含1和2』时,不仅意味着1和2都是整数,而且这个『2』必须得是『1 1=2』的那个『2』。也就是说,我们平时使用的『整数』一词,不仅是指那些数字,而且还蕴含了数字之间的关系(即代数结构)。
所以,为了保证有理数包含整数,他们的运算必须一致,否则这个『整数』就不是我们通常说的那个『整数』了。
有了有理数之后,我们可以把它们扩充为实数。同样地,这里的『扩充』意味着有理数的代数结构不能改变。扩充为实数的方法我这里就不细说了。
现在再看之前的问题:如果定义了『与0的乘积等于1』的数会发生什么呢?
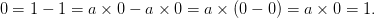

我们可以接着证明所有的实数都等于零,于是整数/有理数/实数的代数结构就被破坏了。所以,试图加入一个『与0的乘积等于1』的数,并不能扩充实数,反而会把实数整个毁掉……
(对学数学的同学多说一句:我们其实可以把环中任意一个对乘法封闭的子集作为分母集合,而对乘法封闭的子集显然是可以包含零的。但是只要包含了零,我们就只能得到一个等价类。具体可以看GTM73第三章第四节。)
第二部分开始了呦
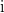 又是怎么出现的呢?
又是怎么出现的呢?回答这个问题之前,我们先来做一个小小的计算:
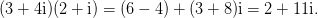
没问题吧?好,看来大家都知道虚数单位
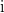 是什么……好的,从现在开始,我们要假装自己不知道虚数单位
是什么……好的,从现在开始,我们要假装自己不知道虚数单位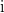 ,只知道实数。
,只知道实数。接下来我们回顾一点点初中的知识:多项式加法、减法、乘法和因式分解。
多项式加法就比如:
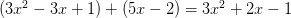 ,减法类似;
,减法类似;多项式乘法就比如:
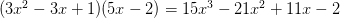 ;
;因式分解就比如:
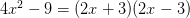 ,这些大家都还记得吧=w=
,这些大家都还记得吧=w=顺便提醒一下:多项式除以多项式不一定是多项式,比如
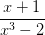 就不是多项式。
就不是多项式。所以,两个(实系数)多项式做加法、减法、乘法之后仍然是(实系数)多项式。
(于是我们说实系数多项式构成了一个环,记作
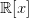 . )
. )(啊,不要被『环』这个奇怪的词吓到,简单说来『环』就是一个可以做加法、减法、乘法的集合。整数、有理数、实数等等都是环。)
好的,接下来我们来讨论因式分解=w=
再看一眼之前的例子,
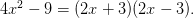
这里我们把一个二次多项式分解为两个一次多项式的乘积,而一次多项式显然不可能再继续被分解为两个多项式的乘积,除非其中一个是常数。于是,我们就说一次多项式是『不可约』的。
相对应地,
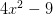 可以被分解为两个次数更低的多项式的乘积,我们就说它是『可约』的。
可以被分解为两个次数更低的多项式的乘积,我们就说它是『可约』的。那么二次多项式有不可约的吗?有,比如
 就不可约。(别忘了我们现在只知道实数!只知道实数!只知道实数!)
就不可约。(别忘了我们现在只知道实数!只知道实数!只知道实数!)没事,
 不可约,那我们就不要它了╭(╯^╰)╮
不可约,那我们就不要它了╭(╯^╰)╮
 』??
』??『不要
 』的意思就是:把所有的
』的意思就是:把所有的 都换成零。
都换成零。我们来看看这样会发生什么。举个例子,比如我们知道:
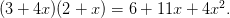
然后我们把所有高冷的
 都找出来:
都找出来: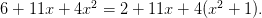
接着,我们把高冷的
 换成零:
换成零: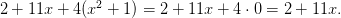
所以,当我们把
 换成零之后,运算结果就变成了:
换成零之后,运算结果就变成了: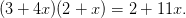
诶嘿,是不是有点眼熟?再看看一开始复数乘法的例子:
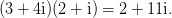
我们发现,把所有
 换成零之后,多项式的乘法就跟复数的乘法一样了!
换成零之后,多项式的乘法就跟复数的乘法一样了!这不是巧合。
不妨设想一下,假如有个人只知道实数而不知道复数,我们如何向他解释
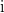 是什么呢?
是什么呢?我们会说:
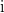 就是一个平方等于
就是一个平方等于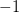 的数,也就是说,
的数,也就是说,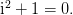
这不正是我们之前做的事情吗?
我们先在实数中加入了一个奇怪的『数』,记作
 ,接着把所有
,接着把所有 都换成零。
都换成零。所以,把实系数多项式环
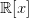 中所有
中所有 换成零,
换成零, 就变得跟
就变得跟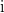 一样了,于是我们就可以得到复数(域)了。
一样了,于是我们就可以得到复数(域)了。复数域就是这么来的。(当然也可以直接定义,这里只讲代数方法。)
用数学语言来说,『把所有
 换成零』这个操作叫『模掉
换成零』这个操作叫『模掉 生成的理想』。
生成的理想』。所谓『
 生成的理想』,在这里就是指一切
生成的理想』,在这里就是指一切 的倍数,记作
的倍数,记作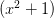 . 因为
. 因为 变为零,那么它的倍数肯定都变为零了嘛。所以
变为零,那么它的倍数肯定都变为零了嘛。所以 所有的倍数,即
所有的倍数,即 生成的理想,都被『模掉』啦。
生成的理想,都被『模掉』啦。写成数学语言就是:
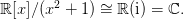
这个『模掉理想』的操作并不局限于
 . 实际上,我们把任何一个不可约多项式生成的理想模掉,都相当于是在原来的数域中加入了该多项式的根。
. 实际上,我们把任何一个不可约多项式生成的理想模掉,都相当于是在原来的数域中加入了该多项式的根。当然,我们一般用这个方法扩张有理数域
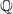 而不是实数域
而不是实数域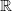 ,因为
,因为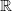 扩张一步之后得到复数域
扩张一步之后得到复数域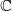 ,就没法再继续这样扩张了(因为
,就没法再继续这样扩张了(因为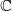 是代数闭域),而
是代数闭域),而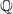 有很多有趣的扩张。
有很多有趣的扩张。举个例子,
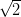 不在有理数域
不在有理数域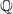 中,而它是
中,而它是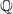 上的不可约多项式
上的不可约多项式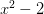 的根,所以我们如果想把
的根,所以我们如果想把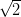 加进
加进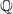 中,我们就把有理系数多项式环
中,我们就把有理系数多项式环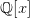 模掉
模掉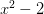 生成的理想,也就是:
生成的理想,也就是: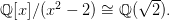
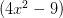 会怎么样?
会怎么样?额,那就会得到一个很奇怪的东西……想一想,由于
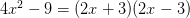 ,我们把
,我们把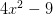 换成零,却没有把它的因子
换成零,却没有把它的因子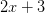 和
和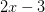 换成零。这就意味着,将会有两个不是零的数乘起来是零……这样的环性质就太差了(连整环都不是),并不是原来数域的扩张。
换成零。这就意味着,将会有两个不是零的数乘起来是零……这样的环性质就太差了(连整环都不是),并不是原来数域的扩张。爱过,不可约,理想已被模掉,不是巧合……
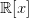 中模掉
中模掉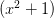 就相当于是在
就相当于是在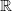 中加入了
中加入了 的根
的根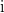 ,可是为什么不是加入
,可是为什么不是加入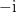 呢?
呢?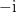 也是
也是 的根啊。
的根啊。啊,这是个好问题。简单一点的回答就是,你在
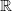 中加入
中加入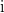 或
或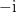 ,得到的都是复数域
,得到的都是复数域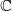 . 更深层次的原因是,不可约多项式的根在代数上是没有办法区分的,加入『不同』的根,得到的扩域在代数上没有区别(同构)——这是伽罗瓦理论告诉我们的。不过在这里我就不展开说了。
. 更深层次的原因是,不可约多项式的根在代数上是没有办法区分的,加入『不同』的根,得到的扩域在代数上没有区别(同构)——这是伽罗瓦理论告诉我们的。不过在这里我就不展开说了。就这样了!

— THE END —

评论
