LeetCode刷题实战37：解数独-技术圈

算法的重要性，我就不多说了吧，想去大厂，就必须要经过基础知识和业务逻辑面试+算法面试。所以，为了提高大家的算法能力，这个公众号后续每天带大家做一道算法题，题目就从LeetCode上面选！

今天和大家聊的问题叫做 解数独，我们先来看题面：

https://leetcode-cn.com/problems/valid-sudoku/

Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfy all of the following rules:
Each of the digits 1-9 must occur exactly once in each row.
Each of the digits 1-9 must occur exactly once in each column.
Each of the the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.
Empty cells are indicated by the character '.'.

题意

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。

数字 1-9 在每一列只能出现一次。

数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 '.' 表示。

题解

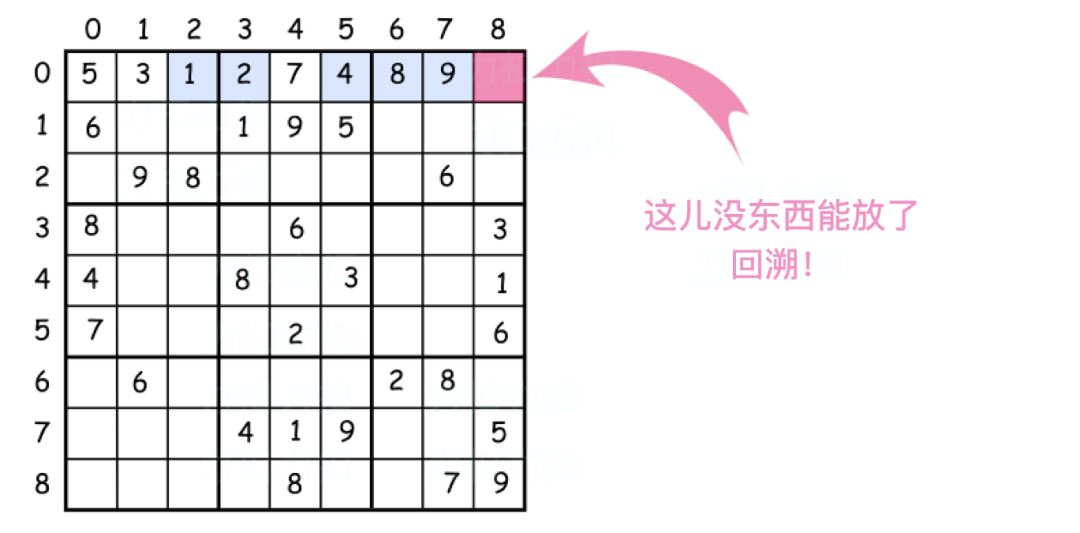
回溯法解数独

让我们想象一下已经成功放置了几个数字在数独上。

但是该组合不是最优的并且不能继续放置数字了。该怎么办？回溯。

意思是回退，来改变之前放置的数字并且继续尝试。如果还是不行，再次回溯。

数独首先行，列，还有 3*3 的方格内数字是 1~9 不能重复。

声明布尔数组，表明行列中某个数字是否被使用了，被用过视为 true，没用过为 false。

初始化布尔数组，表明哪些数字已经被使用过了。

尝试去填充数组，只要行，列，还有 3*3 的方格内出现已经被使用过的数字，我们就不填充，否则尝试填充。

如果填充失败，那么我们需要回溯。将原来尝试填充的地方改回来。

递归直到数独被填充完成。

class Solution {
    public void solveSudoku(char[][] board) {
        // 三个布尔数组 表明 行, 列, 还有 3*3 的方格的数字是否被使用过
        boolean[][] rowUsed = new boolean[9][10];
        boolean[][] colUsed = new boolean[9][10];
        boolean[][][] boxUsed = new boolean[3][3][10];
        // 初始化
        for(int row = 0; row < board.length; row++){
            for(int col = 0; col < board[0].length; col++) {
                int num = board[row][col] - '0';
                if(1 <= num && num <= 9){
                    rowUsed[row][num] = true;
                    colUsed[col][num] = true;
                    boxUsed[row/3][col/3][num] = true;
                }
            }
        }
        // 递归尝试填充数组
        recusiveSolveSudoku(board, rowUsed, colUsed, boxUsed, 0, 0);
    }
    
    private boolean recusiveSolveSudoku(char[][]board, boolean[][]rowUsed, boolean[][]colUsed, boolean[][][]boxUsed, int row, int col){
        // 边界校验, 如果已经填充完成, 返回true, 表示一切结束
        if(col == board[0].length){
            col = 0;
            row++;
            if(row == board.length){
                return true;
            }
        }
        // 是空则尝试填充, 否则跳过继续尝试填充下一个位置
        if(board[row][col] == '.') {
            // 尝试填充1~9
            for(int num = 1; num <= 9; num++){
                boolean canUsed = !(rowUsed[row][num] || colUsed[col][num] || boxUsed[row/3][col/3][num]);
                if(canUsed){
                    rowUsed[row][num] = true;
                    colUsed[col][num] = true;
                    boxUsed[row/3][col/3][num] = true;
                    
                    board[row][col] = (char)('0' + num);
                    if(recusiveSolveSudoku(board, rowUsed, colUsed, boxUsed, row, col + 1)){
                        return true;
                    }
                    board[row][col] = '.';
                    
                    rowUsed[row][num] = false;
                    colUsed[col][num] = false;
                    boxUsed[row/3][col/3][num] = false;
                }
            }
        } else {
            return recusiveSolveSudoku(board, rowUsed, colUsed, boxUsed, row, col + 1);
        }
        return false;
    }
}