八十、归并排序及其分而治之思想

「@Author：Runsen」

❝

编程的本质来源于算法，而算法的本质来源于数学，编程只不过将数学题进行代码化。「---- Runsen」

❞

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

分治算法

分治法是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题 直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。（百度百科）

利用分治策略求解时，所需时间取决于分解后子问题的个数、子问题的规模大小等因素，而二分法，由于其划分的简单和均匀的特点，是经常采用的一种有效的方法，例如二分法检索。

分治算法的基本思想：是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。

分治法所能解决的问题一般具有以下几个特征：

原问题于分解成的小问题具有相同的模式，原问题分解成的小问题可以独立求解，子问题之间没有相关性。

具有分解终止条件，当问题足够小时，可以之间求解，分解出的子问题的解可以合并为该问题的解

基本步骤

• 分解，将要解决的问题划分成若干规模较小的同类问题；
• 求解，当子问题划分得足够小时，用较简单的方法解决；
• 合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

具体伪代码如下：

if (问题不可分):
    返回解
else:
    从原问题中划出含一半运算对象的子问题1；
    递归调用分治法过程，求出解1；
    从原问题中划出含另一半运算对象的子问题2；   
    递归调用分治法过程，求出解2；
    将解1、解2组合成整个问题的解；  

归并排序

分治算法问题求解，一个是二分搜索，一个就是归并排序。

归并排序其实要做两件事：

「拆分」：核心问题是确定拆分位置即可，我们利用左右元素索引之和除2即可，也就是：mid = (left + right)/2，指导拆分到子序列仅仅存在一个元素的基本情形。

「合并」：merge 是归并排序的核心，将两个已排序子序列合并为一个排序序列的过程。当子序列中仅存在一个元素时，可视为子序列已经排序，因此我们的合并是从两个单一元素子序列开始的。

当子序列存在多个元素时，我们需要逐个得到当前最小元素，进而完成整体排序，过程中我们需要一个临时区来存储已排序的部分。

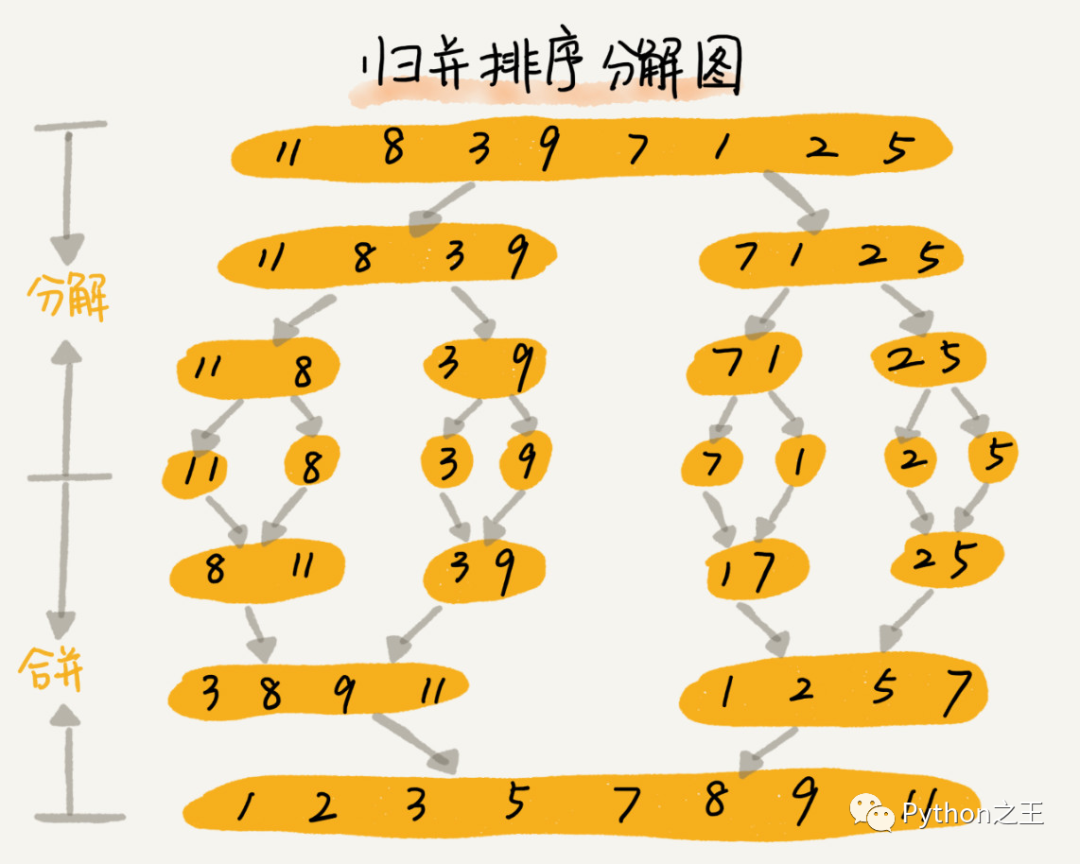
最后将两个区间合并为一个有序的区间，你会怎么思考呢？

这个非常简单，只要从比较二个数列的第一个数，谁小就先取谁，取了后就在对应数列中删除这个数。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可。

'''
@Author：Runsen
@WeChat：RunsenLiu
@微信公众号：Python之王
@CSDN：https://blog.csdn.net/weixin_44510615
@Github：https://github.com/MaoliRUNsen
@Date：2020/12/21
'''
def merge(left, right):  # 合并两个有序数组
    l, r = 0, 0
    result = []
    while l < len(left) and r < len(right):
        if left[l] <= right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]
    result += right[r:]
    return result


def merge_sort(nums):
    if len(nums) <= 1:
        return nums
    num = len(nums) >> 1  #位运算取中间
    left = merge_sort(nums[:num])
    right = merge_sort(nums[num:])
    return merge(left, right)
    
    
if __name__ == '__main__':
    nums = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print(merge_sort(nums))    

[17, 20, 26, 31, 44, 54, 55, 77, 93]

归并排序的运行时间最差、最好和平均都是 O(NlogN)，但是归并排序并没有像快排那样，应用广泛，这是为什么呢？因为它有一个致命的“弱点”，那就是归并排序不是原地排序算法。它需要额外的存储空间，空间复杂度为 O(N)。

「这世上没有天才，你若对得起时间，时间便对得起你。关注我们，每天进步一点点，利用碎片化时间学习。」

❝

本文已收录 GitHub，传送门~^[1] ，里面更有大厂面试完整考点，欢迎 Star。

❞

Reference