数组排序算组之归并排序
归并排序(Merge Sort)是数组排序算法中一种常见的算法,其主要思想为经典的“分治思想”。本文将介绍数组排序算法中的归并排序,并介绍其相关应用。
本文的文章结构分布如下:
从合并两个有序数组讲起
数组归并排序
合并K个有序数组
归并排序的应用
首先,我们从合并两个有序数组开始,这是归并排序的基础。
从合并两个有序数组讲起
假设我们有两个已经排好序(不妨假设为升序)的数组nums1和nums2,如何将这两个数组合并起来呢?其实想法是比较简单的,就是用双指针法。用两个指针分别指向这两个数组,然后分别从头到尾遍历,需要注意比较两个指针指向的数字大小,具体算法如下:
假设合并后的数字为
sorted,初始化为空数组;如果指向数组
nums1的指针已经达到数组nums1的末尾,则将数组nums2中的剩余元素依次添加至sorted中;如果指向数组
nums2的指针已经达到数组nums2的末尾,则将数组nums1中的剩余元素依次添加至sorted中;如果两个指针都没有达到数组的结尾,则比较该指针指向的数字,数字小的添加至
sorted中,同时该指针向后移动一位。
我们以数组[1,2, 3]和[2,5,6]为例,其合并过程如下图: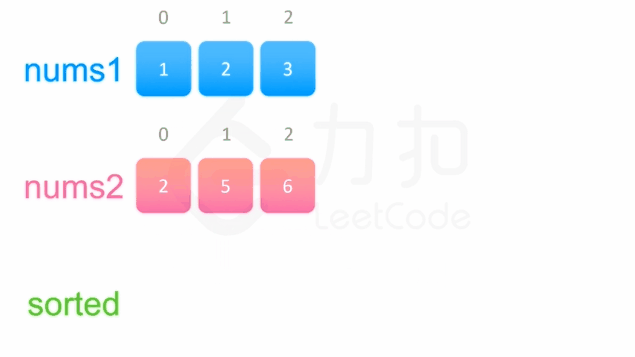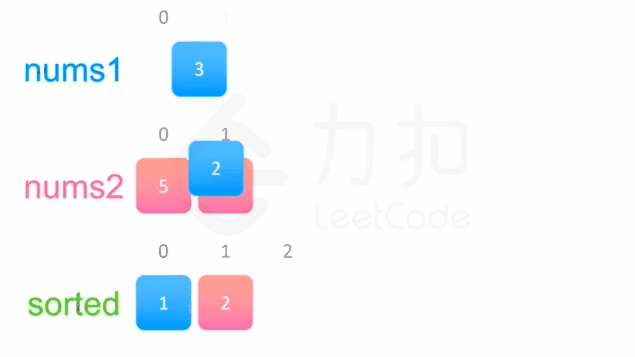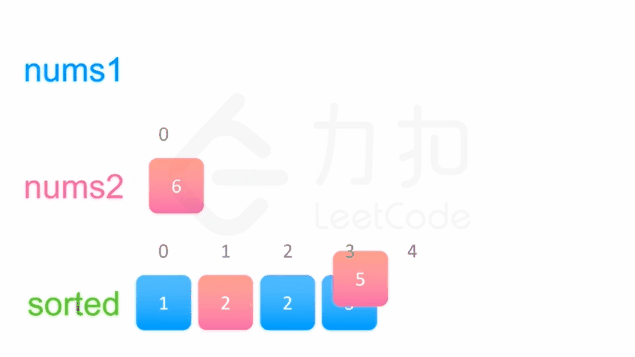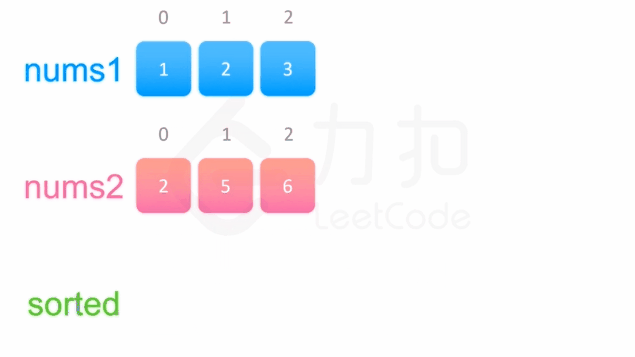
两个有序数组的合并 该算法的Python程序如下:
def merge(nums1, nums2):
result = []
m, n = len(nums1), len(nums2)
p1, p2 = 0, 0
while p1 < m or p2 < n:
if p1 == m:
result.append(nums2[p2])
p2 += 1
elif p2 == n:
result.append(nums1[p1])
p1 += 1
elif nums1[p1] < nums2[p2]:
result.append(nums1[p1])
p1 += 1
else:
result.append(nums2[p2])
p2 += 1
return result
if __name__ == '__main__':
a = [1, 2, 3]
b = [2, 5, 6]
sol = merge(a, b)
print('arrays: {} and {}, merge: {}'.format(a, b, sol))
a = [1, 2]
b = [2, 5, 6]
sol = merge(a, b)
print('arrays: {} and {}, merge: {}'.format(a, b, sol))
a = [1, 2, 3, 4]
b = [2, 5, 6]
sol = merge(a, b)
print('arrays: {} and {}, merge: {}'.format(a, b, sol))
运行结果如下:
arrays: [1, 2, 3] and [2, 5, 6], merge: [1, 2, 2, 3, 5, 6]
arrays: [1, 2] and [2, 5, 6], merge: [1, 2, 2, 5, 6]
arrays: [1, 2, 3, 4] and [2, 5, 6], merge: [1, 2, 2, 3, 4, 5, 6]
数组归并排序
经过上述介绍,我们已经知晓如何合并两个有序数组了。接下来,我们讨论如何对数组进行排序。利用“分而治之”的想法,我们将原始数组result分为两部分left和right,两部分长度尽可能接近。如果left和right已经排好序了,那么将这两个排序数组合并即可。问题就变为如何将left和right排序?但此时,我们发现left和right的长度大约为原始元素result的一半,因此我们可以不停地left和right拆分,直到它们的长度为0或者1,那么此时这两个数组已经排好序了,最后我们再将分拆后的数组自下而上地进行合并结果即可。
我们以数组[6,5,12,10,9,1]为例,具体演示该过程:
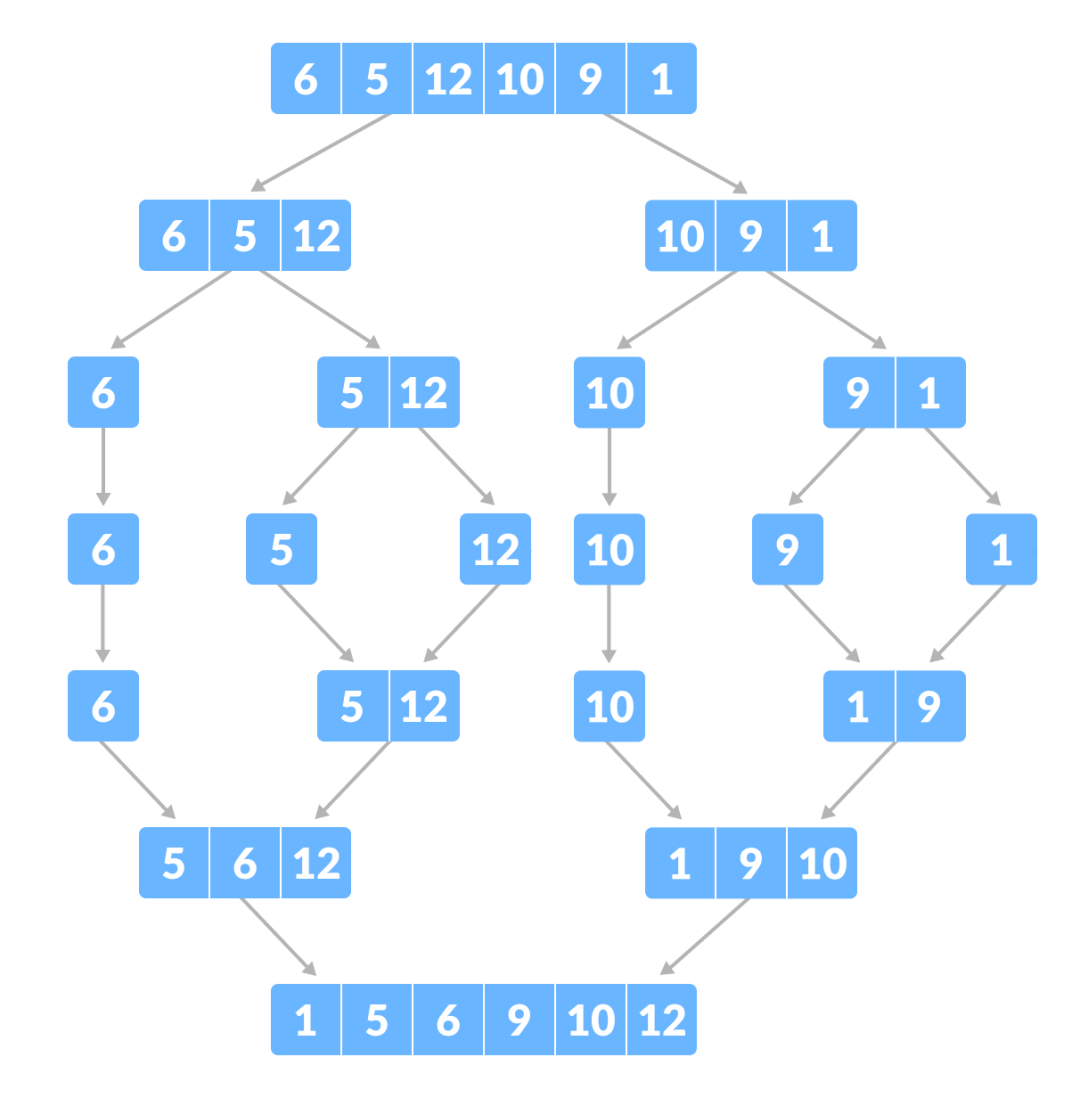
归并排序的Python实现代码如下(merge函数参考前面代码):
def merge_sort(lst):
if len(lst) <= 1:
return lst # 从递归中返回长度为1的序列
middle = len(lst) // 2
left = merge_sort(lst[:middle]) # 通过不断递归,将原始序列拆分成n个小序列
right = merge_sort(lst[middle:])
return merge(left, right)
if __name__ == '__main__':
a = [6, 5, 12, 10, 9, 1]
result = merge_sort(a)
print('array: {}, after merge sort: {}'.format(a, result))
a = [6, 5, 12, 10]
result = merge_sort(a)
print('array: {}, after merge sort: {}'.format(a, result))
a = [1, 2, 3, 2, 5, 6]
result = merge_sort(a)
print('array: {}, after merge sort: {}'.format(a, result))
运行结果如下:
array: [6, 5, 12, 10, 9, 1], after merge sort: [1, 5, 6, 9, 10, 12]
array: [6, 5, 12, 10], after merge sort: [5, 6, 10, 12]
array: [1, 2, 3, 2, 5, 6], after merge sort: [1, 2, 2, 3, 5, 6]
数组的归并排序算法的时间复杂度为O(n*log n), 空间复杂度为O(n),其中n代表数组的长度,并且归并排序算法是稳定的。
合并K个有序数组
假如我们将合并两个有序数组扩展成K个有序数组(不妨假设都是升序排列)的情形呢?其实,我们也可以借鉴数组的归并排序的思想。
我们将长度为K的有序数组列表,按中间数组分成长度大致相同的两个数组列表,利用分拆、合并的办法可以将这两个数组列表合并(此时问题的数组列表规模大致为原先的一半),再合并生成的这两个列表即可。
具体实现的Python代码如下:
def merge_k_sort(lists):
n = len(lists)
if n == 0:
return []
elif n == 1:
return lists[0]
else:
middle = n // 2
left = merge_k_sort(lists[:middle])
right = merge_k_sort(lists[middle:])
return merge(left, right)
if __name__ == '__main__':
lists = [[1, 2], [3, 5], [7, 9]]
result = merge_k_sort(lists)
print('lists: {}, after merge: {}'.format(lists, result))
lists = [[1, 2], [3, 5], [7, 9], [4, 10]]
result = merge_k_sort(lists)
print('lists: {}, after merge: {}'.format(lists, result))
lists = [[1, 2], [3, 5], [7, 9], [4, 10], [6, 8, 12]]
result = merge_k_sort(lists)
print('lists: {}, after merge: {}'.format(lists, result))
运行结果如下:
lists: [[1, 2], [3, 5], [7, 9]], after merge: [1, 2, 3, 5, 7, 9]
lists: [[1, 2], [3, 5], [7, 9], [4, 10]], after merge: [1, 2, 3, 4, 5, 7, 9, 10]
lists: [[1, 2], [3, 5], [7, 9], [4, 10], [6, 8, 12]], after merge: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12]
其实,我们可以将数组的排序转化为合并K个数组问题。我们只需要将数组的每个元素单独组成一个列表,长度为1,则合并这些长度为1的列表即可,因为它们已经排好序了!
if __name__ == '__main__':
nums = [6, 5, 12, 10, 9, 1]
lists = [[x] for x in nums]
result = merge_k_sort(lists)
print('array: {}, result: {}'.format(nums, result))
归并排序的应用
该部分将介绍归并排序的应用,主要介绍数组的逆序对问题。归并排序的应用主要如下:
链表排序
数组的逆序对数量问题
外部排序(External Sorting)
其中链表排序也可以用归并排序思想实现,其大致思路差不多,主要是链表本身与数组的数据结构上的差异,其基础仍然是合并两个有序链表。
重点介绍数组的逆序对数量问题。所谓数组的逆序对,指的是对于数组a的两个下标位置i和j,满足i
数组[8,4,2,1],其逆序对数量为6;
数组[1, 20, 6, 4, 5],其逆序对数量为5;
我们也用归并排序思想也解决数组的逆序对数量问题。我们考虑以下情况:

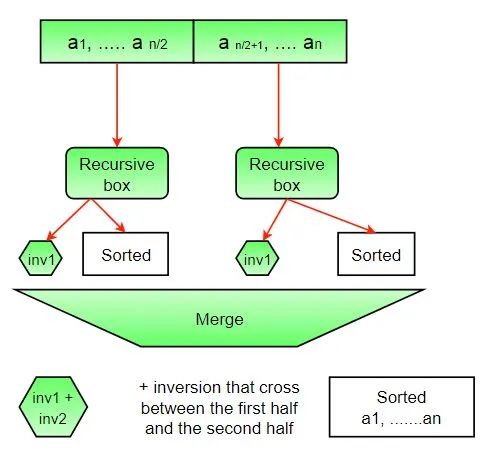
对于数组a,将其拆分成inv1和inv2,那么数组a的逆序对数量,应该是inv1的逆序对数量加上inv2的逆序对数量以及inv1和inv2按升序排列后合并时产生的逆序对数量。
将inv1和inv2升序排列,可以用归并排序思想。那么为什么要对inv1和inv2按升序排列呢?这是因为,如果将inv1和inv2升序排序后,如果inv1中的位置i和inv2中的位置j满足inv1[i]>inv2[j],那么inv1在i后面的元素都大于inv2[j],这样就方便计算了。
数组的逆序对数量问题的Python实现代码如下:
# Function to Use Inversion Count
def mergeSort(arr, n):
temp_arr = [0] * n
return _mergeSort(arr, temp_arr, 0, n - 1)
# This Function will use MergeSort to count inversions
def _mergeSort(arr, temp_arr, left, right):
inv_count = 0
if left < right:
mid = (left + right) // 2
inv_count += _mergeSort(arr, temp_arr, left, mid)
inv_count += _mergeSort(arr, temp_arr, mid + 1, right)
inv_count += merge(arr, temp_arr, left, mid, right)
return inv_count
# This function will merge two subarrays in a single sorted subarray
def merge(arr, temp_arr, left, mid, right):
i = left # Starting index of left subarray
j = mid + 1 # Starting index of right subarray
k = left # Starting index of to be sorted subarray
inv_count = 0
while i <= mid and j <= right:
if arr[i] <= arr[j]:
temp_arr[k] = arr[i]
k += 1
i += 1
else:
temp_arr[k] = arr[j]
inv_count += (mid - i + 1)
k += 1
j += 1
# Copy the remaining elements of left subarray into temporary array
while i <= mid:
temp_arr[k] = arr[i]
k += 1
i += 1
# Copy the remaining elements of right subarray into temporary array
while j <= right:
temp_arr[k] = arr[j]
k += 1
j += 1
# Copy the sorted subarray into Original array
for loop_var in range(left, right + 1):
arr[loop_var] = temp_arr[loop_var]
return inv_count
if __name__ == '__main__':
arr = [1, 20, 6, 4, 5]
# arr = [8, 4, 2, 1]
n = len(arr)
result = mergeSort(arr, n)
print("Number of inversions are", result)
总结
本文主要介绍了数组排序中的归并排序思想及其在数组逆序对中的应用。
欢迎大家访问我的CSDN博客:https://blog.csdn.net/jclian91,后续我的文章将全部在上面展示,个人的微信公众号将另作他用,届时将不会在该公众号上发布技术文章。
参考网址:
合并两个有序数组: https://leetcode.cn/problems/merge-sorted-array/description/
剑指 Offer 51. 数组中的逆序对: https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/
Merge Sort Algorithm: https://www.geeksforgeeks.org/merge-sort/
Inversion count in Array using Merge Sort: https://www.geeksforgeeks.org/inversion-count-in-array-using-merge-sort/
Merge Sort Algorithm: https://www.programiz.com/dsa/merge-sort
