AVL树的C++实现
首先,AVL 树是二叉查找树,即任意一个节点的左子结点小于当前结点,右子结点大于当前结点。
然后,AVL 树是平衡树,任意一个结点的左子树和右子树高度差的绝对值小于等于 1。
定义
template <typename T>
class AVLTreeNode {
public:
T key;
int height = 1; //树高
AVLTreeNode* l;
AVLTreeNode* r;
AVLTreeNode(T _key, AVLTreeNode* _l, AVLTreeNode* _r) : key(_key), l(_l), r(_r) {}
};
template <typename T>
class AVLTree {
public:
AVLTreeNode<T>* root;
AVLTree() { this->root = nullptr; }
~AVLTree();
int height(AVLTreeNode<T>* tree);
int height();
void insert(T key);
void remove(T key);
AVLTreeNode<T>* find(T key);
void print();
private:
AVLTreeNode<T>* LLRotation(AVLTreeNode<T>* k2);
AVLTreeNode<T>* LRRotation(AVLTreeNode<T>* k2);
AVLTreeNode<T>* RRRotation(AVLTreeNode<T>* k2);
AVLTreeNode<T>* RLRotation(AVLTreeNode<T>* k2);
AVLTreeNode<T>* insert(T key, AVLTreeNode<T>* root);
AVLTreeNode<T>* remove(AVLTreeNode<T>* del, AVLTreeNode<T>* root);
AVLTreeNode<T>* find(T key, AVLTreeNode<T>* root);
AVLTreeNode<T>* findmax(AVLTreeNode<T>* root);
AVLTreeNode<T>* findmin(AVLTreeNode<T>* root);
};
旋转
AVL 树的旋转有 4 种,LL,RR,LR,RL。
LL
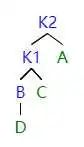
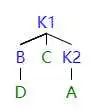
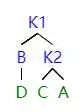
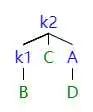
如图所示,当左子树的左子树影响平衡的时候,我们需要进行 LL 旋转。
首先,我们把 k1 提起来 (就像提绳子一样),这时候 k1 是根结点。但是这时候会发现 k1 有三个子节点,不符合二叉树的定义。同时又因为 k2 刚好被转过去,没有左子结点。所以我们就把 k1 原先的右子树给 k2 当左子树。
因为 k2 之前是根节点,所以 k2>k1 的右子结点 > k1,如上操作之后,符合 AVL 树的定义。
每次旋转之后都重新计算树高。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::LLRotation(AVLTreeNode<T>* k2) {
AVLTreeNode<T>* k1;
k1 = k2->l;
k2->l = k1->r;
k1->r = k2;
k2->height = max(height(k2->l), height(k2->r)) + 1;
k1->height = max(height(k1->l), k2->height) + 1;
return k1;
}
RR
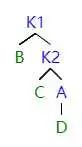
理解 LL 之后,RR 就很好理解。
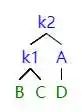
当右子树的右子树影响平衡之后,我们首先把 k2 提起来,现在 k1 缺少右子结点,我们就把 k2 之前的左子树给过去。
因为 k2>k2 的左子结点 > k1,操作之后符合 AVL 树的定义。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::RRRotation(AVLTreeNode<T>* k1) {
AVLTreeNode<T>* k2;
k2 = k1->r;
k1->r = k2->l;
k2->l = k1;
k1->height = max(height(k1->l), height(k1->r)) + 1;
k2->height = max(height(k2->r), k1->height) + 1;
return k2;
}
LR
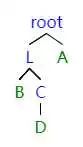
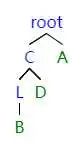
当左子树的右子树影响平衡的时候,我们对右子树进行一次 RR 旋转,之后就转化为 LL 旋转。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::LRRotation(AVLTreeNode<T>* root) {
root->l = RRRotation(root->l);
return LLRotation(root);
}
RL
理解以上几个之后,RL 也就很好理解了,此处不再赘述,请读者自行思考。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::RLRotation(AVLTreeNode<T>* root) {
root->r = LLRotation(root->r);
return RRRotation(root);
}
插入
我们递归查找插入的位置,回溯的过程中发现不平衡就去进行旋转。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::insert(T key, AVLTreeNode<T>* root) {
if (root == nullptr) {
root = new AVLTreeNode<T>(key, nullptr, nullptr);
}
else if (key < root->key) {//插入到左子树
root->l = insert(key, root->l);
if (height(root->l) - height(root->r) == 2) {
if (key < root->l->key) {
root = LLRotation(root);
}
else {
root = LRRotation(root);
}
}
}
else if (key > root->key) {//插入到右子树
root->r = insert(key, root->r);
if (height(root->r) - height(root->l) == 2) {
if (key > root->r->key) {
root = RRRotation(root);
}
else {
root = RLRotation(root);
}
}
}
root->height = max(height(root->l), height(root->r)) + 1;
return root;
}
template <typename T>
void AVLTree<T>::insert(T key) {
root = insert(key, root);
}
查找和删除
template <typename T>
AVLTreeNode<T>* AVLTree<T>::find(T key) {
return find(key, root);
}
template <typename T>
AVLTreeNode<T>* AVLTree<T>::find(T key, AVLTreeNode<T>* root) {
if (root == nullptr)
return root;
if (key > root->key) {
return find(key, root->r);
}
else if (key < root->key) {
return find(key, root->l);
}
else
return root;
}
template <typename T>
AVLTreeNode<T>* AVLTree<T>::findmax(AVLTreeNode<T>* root) {
if (root->r == nullptr)
return root;
return findmax(root->r);
}
template <typename T>
AVLTreeNode<T>* AVLTree<T>::findmin(AVLTreeNode<T>* root) {
if (root->l == nullptr)
return root;
return findmin(root->l);
}
template <typename T>
AVLTreeNode<T>* AVLTree<T>::remove(AVLTreeNode<T>* del, AVLTreeNode<T>* root) {
//没找到直接返回
if (root == nullptr || del == nullptr)
return root;
if (del->key < root->key) {//需要删除的结点在左子树中
root->l = remove(del, root->l);
if (height(root->r) - height(root->l) == 2) {
if (height(root->r->l) > height(root->r->r)) {
root = RLRotation(root);
}
else {
root = RRRotation(root);
}
}
}
else if (del->key > root->key) {//需要删除的结点在右子树中
root->r = remove(del, root->r);
if (height(root->l) - height(root->r) == 2) {
if (height(root->l->r) > height(root->l->l)) {
root = LRRotation(root);
}
else {
root = LLRotation(root);
}
}
}
else {
//左右子树都不为空,删除后,我们可以用左子树的最大结点或右子树的最小结点来替换这个结点
if (root->l != nullptr && root->r != nullptr) {
if (height(root->l) > height(root->r)) {
//用左子树的最大结点,好处是删除后还是平衡的,无需旋转
AVLTreeNode<T>* mx = findmax(root->l);
root->key = mx->key;
root->l = remove(mx, root->l);
}
else {
//用右子树的最大结点,好处同上
AVLTreeNode<T>* mn = findmin(root->r);
root->key = mn->key;
root->r = remove(mn, root->r);
}
}
else {
AVLTreeNode<T>* tmp = root;
root = (root->l == nullptr) ? root->r : root->l;
delete tmp;
}
}
return root;
}
template <typename T>
void AVLTree<T>::remove(T key) {
root = remove(find(key), root);
}
总结
至于析构,遍历等等的代码和此处不再给出,请参照正常的二叉树操作自行思考。
AVL 树的实现实际上不难,由于各种教材上冗长的介绍,使得我们有一种认为它难的错觉。
评论
