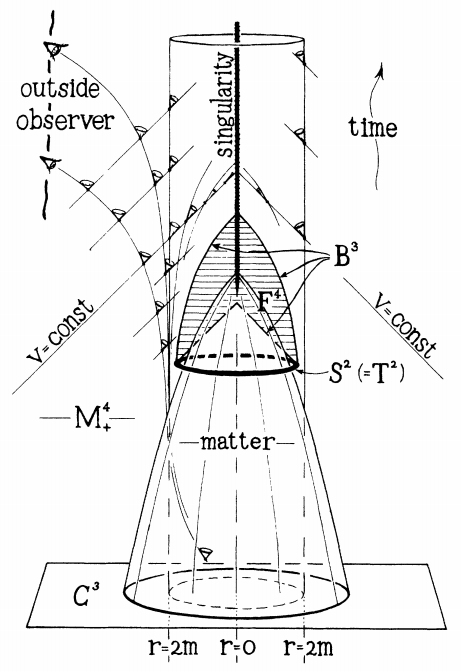
数学家为啥能研究黑洞，还能拿诺贝尔物理学奖？-技术圈

不想看公式就直接看留言。说黑洞，不得不说爱因斯坦提出的广义相对论中的场方程。

R_{\mu \nu}-\frac{1}{2} R g_{\mu \nu}+\Lambda g_{\mu \nu} =\frac{8 \pi G}{c^{4}} T_{\mu \nu}

左侧

右侧

曲率张量听上去是不是很高大上，其实这里指的是 2 阶张量，可以直接用一个矩阵表示。只是它们都是物理量，不受坐标系选择的影响。

爱因斯坦场方程是描述了时空中每一点处能量动量的数量关系，但是每一点的上面那些张量可以不同。用到的背景工具是黎曼几何以及张量分析。

我们可以简单地想象成一张嵌在 3 维空间中的 2 维曲面，然后你在这些面上生活，只是它那里是 4 维的。

上面那个场方程中的张量在时空中每一点可以不同，相当于在每一点配上了好几个矩阵，每点的标量 R 其实也类似，这里省略。可以设想宇宙中每点都有好几把尺子，它们还可以处处不同。

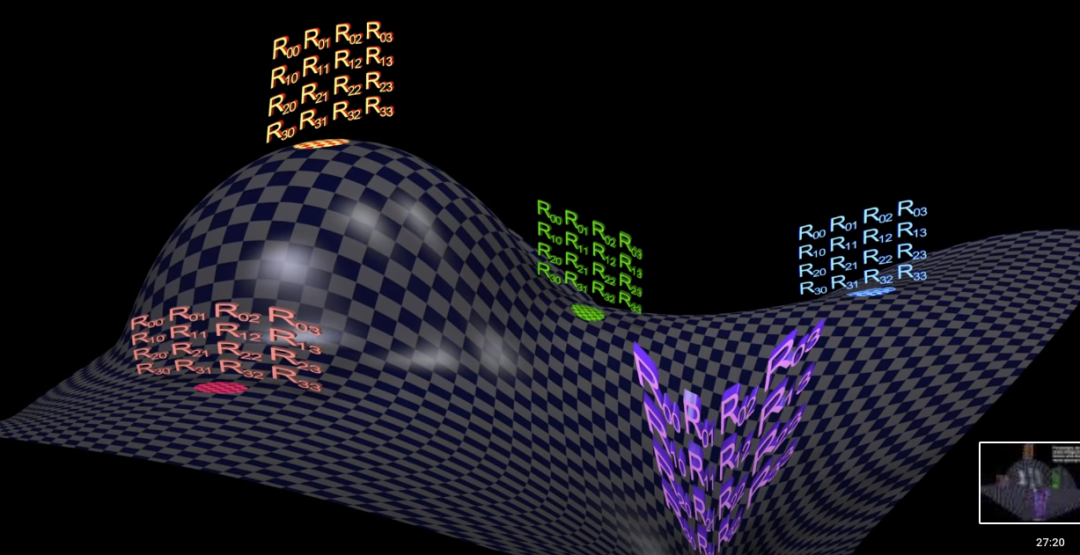
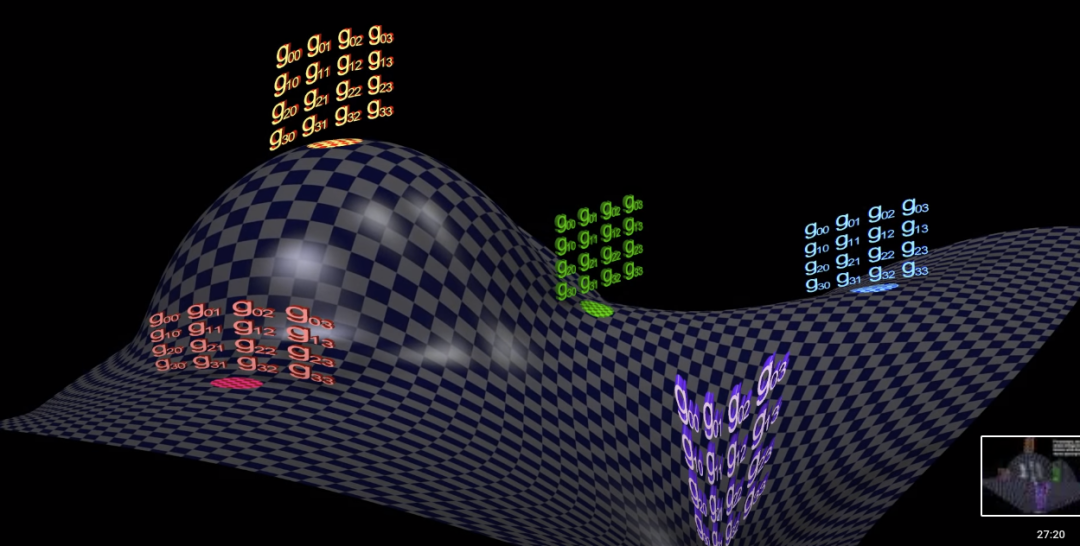
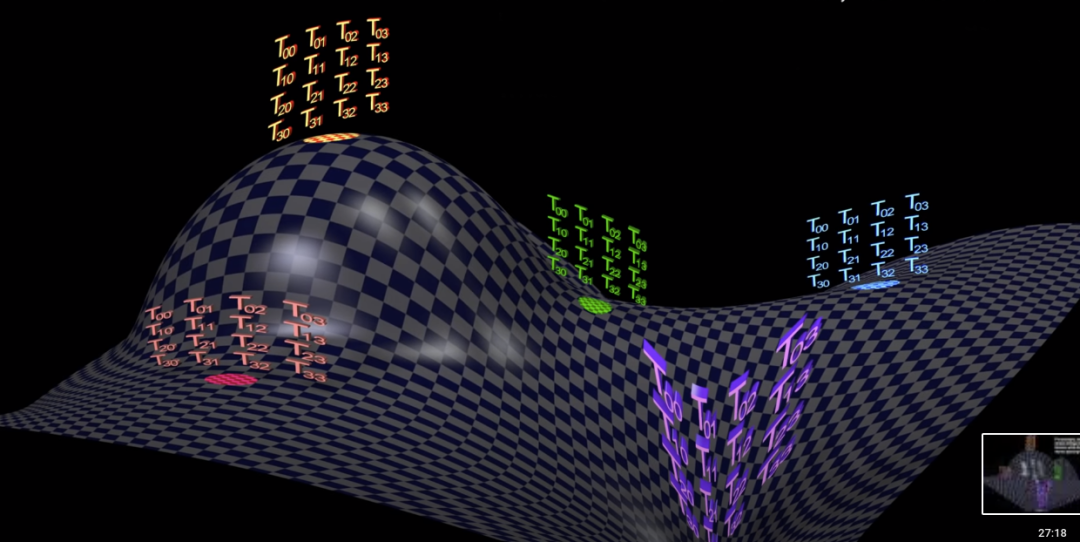
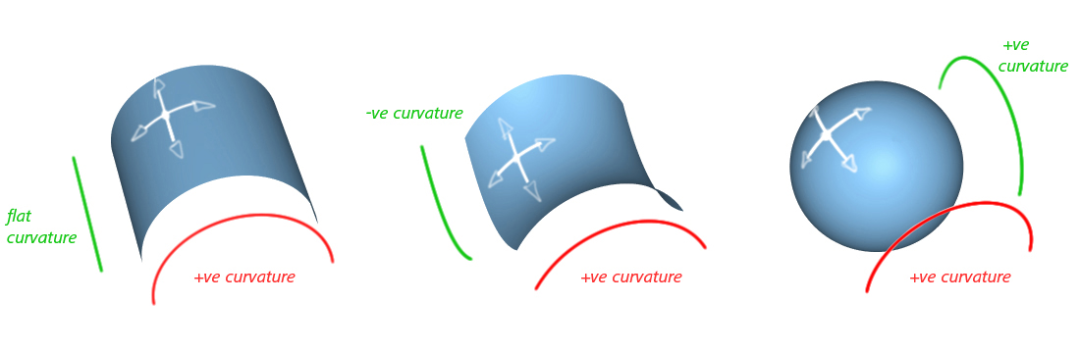
爱因斯坦认为，引力场或者物质的存在导致了时空的弯曲，而时空的弯曲恰恰体现了引力本身。上面的场方程就是把爱因斯坦的这个思想给数量化了。

可是，这个跟黑洞有神马关系？爱因斯坦在场方程中早就想到黑洞这回事了？

这个方程的左边对应时空弯曲，而右边对应物质及其运动。爱因斯坦拍脑袋（上帝给了他灵感吧），再加上一些数学家的帮助，他终于搞定了这个方程。

但是，这相当于只是给时空中每一点下了一些规矩，具体时空是怎么样的，需要求解这个场方程才知道。解方程也意味着构造时空，换句话说，不同的解对应着一个不同的宇宙。那么我们所处的宇宙到底是怎么样的呢？

第一个从数学上求解这个方程的是德国天文物理学家卡尔·施瓦西，他得出，

g = -\left(1-\frac{r_{\mathrm{s}}}{r}\right) c^{2} d t^{2}+\left(1-\frac{r_{\mathrm{s}}}{r}\right)^{-1} d r^{2}+r^{2} g_{\Omega}

其中，，以及。别的咱们不管，就看里面的这一项，

(1-\frac{2 G M}{rc^{2}})^{-1} = \frac{1}{1-\displaystyle\frac{2 G M}{rc^{2}}}

注意它的分母，，万一等于 0 怎么办？别瞎想，小学老师教我们的时候说了呀，分母不能为 0 啊。那怎么办？万一有些情况下这几个数凑一起算出来刚好等于 0，万一碰到一个爱问十万个为什么的小朋友，可咋办办呢？

数学家、物理学家有办法，给它取个名字特殊化就可以了，对，就叫它奇点。史瓦西认为，奇点附近将具有极大的引力，边上任何物质，连光都得被吸进去了。后来美国物理学家惠勒将它命名为黑洞。

那么它存在吗？仔细看，其中的和都是常数，质量也好说，就差了。那么假设我们所在系统中的最大天体，就是说太阳，如果把它压缩到很小很小，例如像新冠病毒那么小，是不是可以达到这个条件呢。这就是所谓的史瓦西半径。

简单计算下其实不需要那么小，大约把太阳压缩到 3 公里就可以了。

爱因斯于 1915 年发布广义相对论，史瓦西在年底就求出了它的第一个真空解。在当时，这也超出了爱因斯坦本人的预期。要知道求解这组非线性偏微分方程是件不容易的事情，而此时的史瓦西还在一战的前线，可惜没多久就英年早逝了。

史瓦西的解最让人振奋的一面是，它从数学上预言了黑洞。注意，是数学上。那么我们实际的宇宙到底有没有黑洞呢？拍脑袋是定不下来的，要么就问上帝，要么根据实际观测来推断。

这次数学家彭罗斯得了诺贝尔奖，是因为他从纯数学的角度研究黑洞，并提出了所谓的奇点定理，从而从理论上去除了对解的对称性要求。

像上面史瓦西等人提出的一些解的存在是严重依赖对称性的，而真实宇宙环境中的对称性会不会有那么完美呢？那么依赖这种解的黑洞是不是不存在呢？天体坍缩是否能满足这个对称性从而形成黑洞呢？

在彭罗斯之前，天文界的主流观点认为黑洞多半是意淫出来的，在我们所处的宇宙中估计是不存在。

而彭罗斯在上世纪六十年代，从纯数学的角度来研究天体物理。他在 1965 年的论文（Gravitational Collapse and Space-Time Singularities）中指出，即使偏离球面对称仍然会出现时空奇点。

也就是说，不管对称不对称之类的要求，最终都会出现一个数学上的奇点，这个奇点就能形成黑洞。从而重新燃起了天文学界对黑洞的热情，促使人们继续去寻找黑洞。