这应该是网上最简单的元学习入门教程了
作者：凉爽的安迪
知乎：https://www.zhihu.com/people/wang-wj-38
「写在前面：迄今为止，本文应该是网上介绍【元学习（Meta-Learning）】」 最通俗易懂的文章了（ 保命），主要目的是想对自己对于元学习的内容和问题进行总结，同时为想要学习Meta-Learning的同学提供一下简单的入门。笔者挑选了经典的paper详读，看了李宏毅老师深度学习课程元学习部分，并附了MAML的代码。为了通俗易懂，我将数学推导和工程实践分开两篇文章进行介绍。~
「如果大家觉得有帮助，可以帮忙点个赞或者收藏一下，这将是我继续分享的动力~」
以下是本文的主要框架：
Introduction Meta Learning 实施——以 MAML 为例 Reptile What's more
1. Introduction
通常在机器学习里，我们会使用某个场景的大量数据来训练模型；然而当场景发生改变，模型就需要重新训练。但是对于人类而言，一个小朋友成长过程中会见过许多物体的照片，某一天，当 Ta（第一次）仅仅看了几张狗的照片，就可以很好地对狗和其他物体进行区分。
元学习 Meta Learning，含义为学会学习，即 learn to learn，就是带着这种对人类这种“学习能力”的期望诞生的。Meta Learning 希望使得模型获取一种“学会学习”的能力，使其可以在获取已有“知识”的基础上快速学习新的任务，如：
让 Alphago 迅速学会下象棋 让一个猫咪图片分类器，迅速具有分类其他物体的能力
「需要注意的是，虽然同样有“预训练”的意思在里面，但是元学习的内核区别于迁移学习（Transfer Learning）」，关于他们的区别，我会在下文进行阐述。
接下来，我们通过对比机器学习和元学习这两个概念的要素来加深对元学习这个概念的理解。
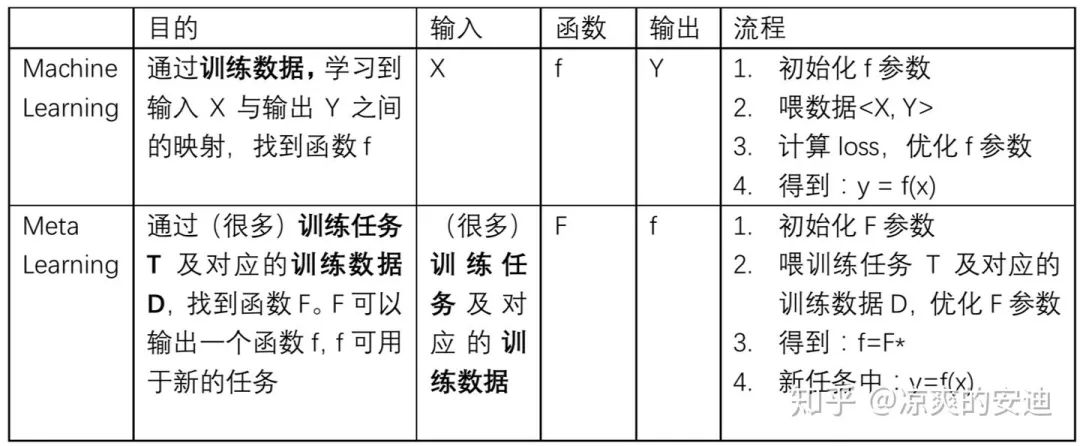
在机器学习中，「训练单位是一条数据」，通过数据来对模型进行优化；数据可以分为训练集、测试集和验证集。在元学习中，训练单位分层级了，「第一层训练单位是任务，也就是说，元学习中要准备许多任务来进行学习，第二层训练单位才是每个任务对应的数据」。
二者的目的都是找一个 Function，只是两个 Function 的功能不同，要做的事情不一样。机器学习中的 Function 直接作用于特征和标签，去寻找特征与标签之间的关联；而元学习中的 Function 是用于寻找新的 f，新的 f 才会应用于具体的任务。「有种不同阶导数的感觉」。又有种**老千层饼的感觉，**你看到我在第二层，你把我想象成第一层，而其实我在第五层。。。
2. Meta Learning 实施——以 MAML 为例
我们先对比机器学习的过程来进一步理解元学习。如下图所示，机器学习的一般过程如下：
设计网络网络结构，如 CNN、RNN 等； 选定某个分布来初始化参数；（以上其实决定了初始的f的长相，选择不同的网络结构或参数相当于定义了不同的f）； 喂训练数据，根据选定的 Loss Function 计算 Loss； 梯度下降，逐步更新 ； 得到最终的 f
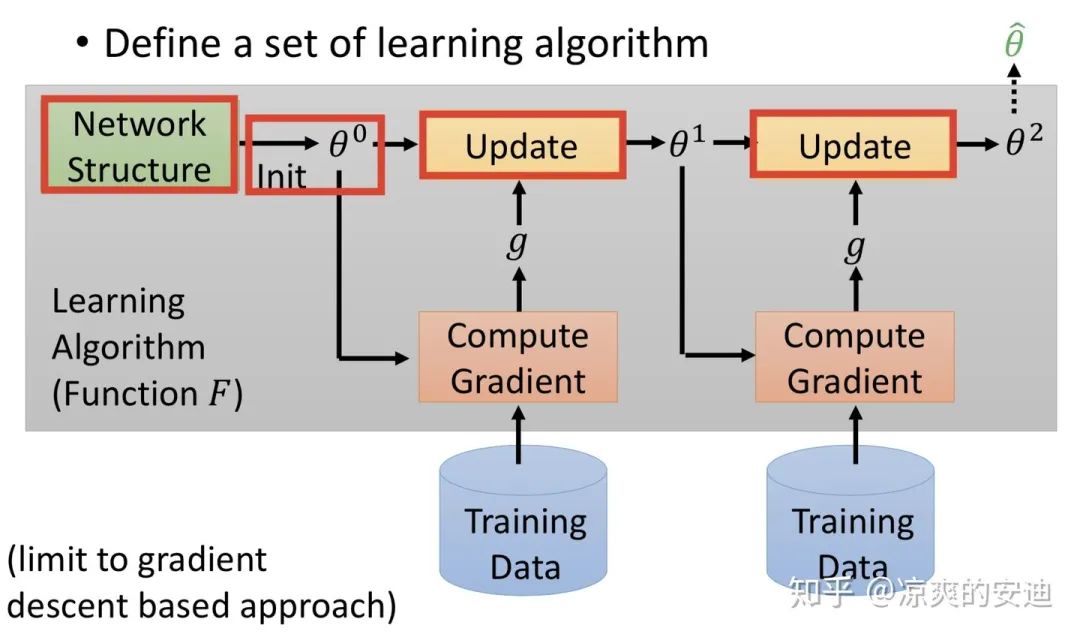
机器学习过程，引自李宏毅《深度学习》
其中，红色方框里的“配置”都是由人为设计的，我们又叫做“超参数“。Meta Learning 中希望把这些配置，如网络结构，参数初始化，优化器等由机器自行设计（注：此处区别于 AutoML，迁移学习（Transfer Learning）和终身学习（Life Long Learning） ），使网络有更强的学习能力和表现。
上文已经提到，「【元学习中要准备许多任务来进行学习，而每个任务又有各自的训练集和测试集】」。我们结合一个具体的任务，来介绍元学习和MAML的实施过程。
有一个图像数据集叫 Omniglot：https://github.com/brendenlake/omniglot。Omniglot 包含 1623 个不同的火星文字符，每个字符包含 20 个手写的 case。这个任务是判断每个手写的 case 属于哪一个火星文字符。
如果我们要进行 N-ways，K-shot（数据中包含 N 个字符类别，每个字符有 K 张图像）的一个图像分类任务。比如 20-ways，1-shot 分类的意思是说，要做一个 20 分类，但是每个分类下只有 1 张图像的任务。我们可以依据 Omniglot 构建很多 N-ways，K-shot 任务，这些任务将作为元学习的任务来源。构建的任务分为训练任务（Train Task），测试任务（Test Task）。特别地，每个任务包含自己的「训练数据、测试数据」，在元学习里，分别称为 「Support Set 和 Query Set」。
「MAML 的目的是获取一组更好的模型初始化参数（即让模型自己学会初始化）」。我们通过（许多）N-ways，K-shot 的任务（训练任务）进行元学习的训练，使得模型学习到“先验知识”（初始化的参数）。这个“先验知识”在新的 N-ways，K-shot 任务上可以表现的更好。
接下来介绍 MAML 的算法流程：
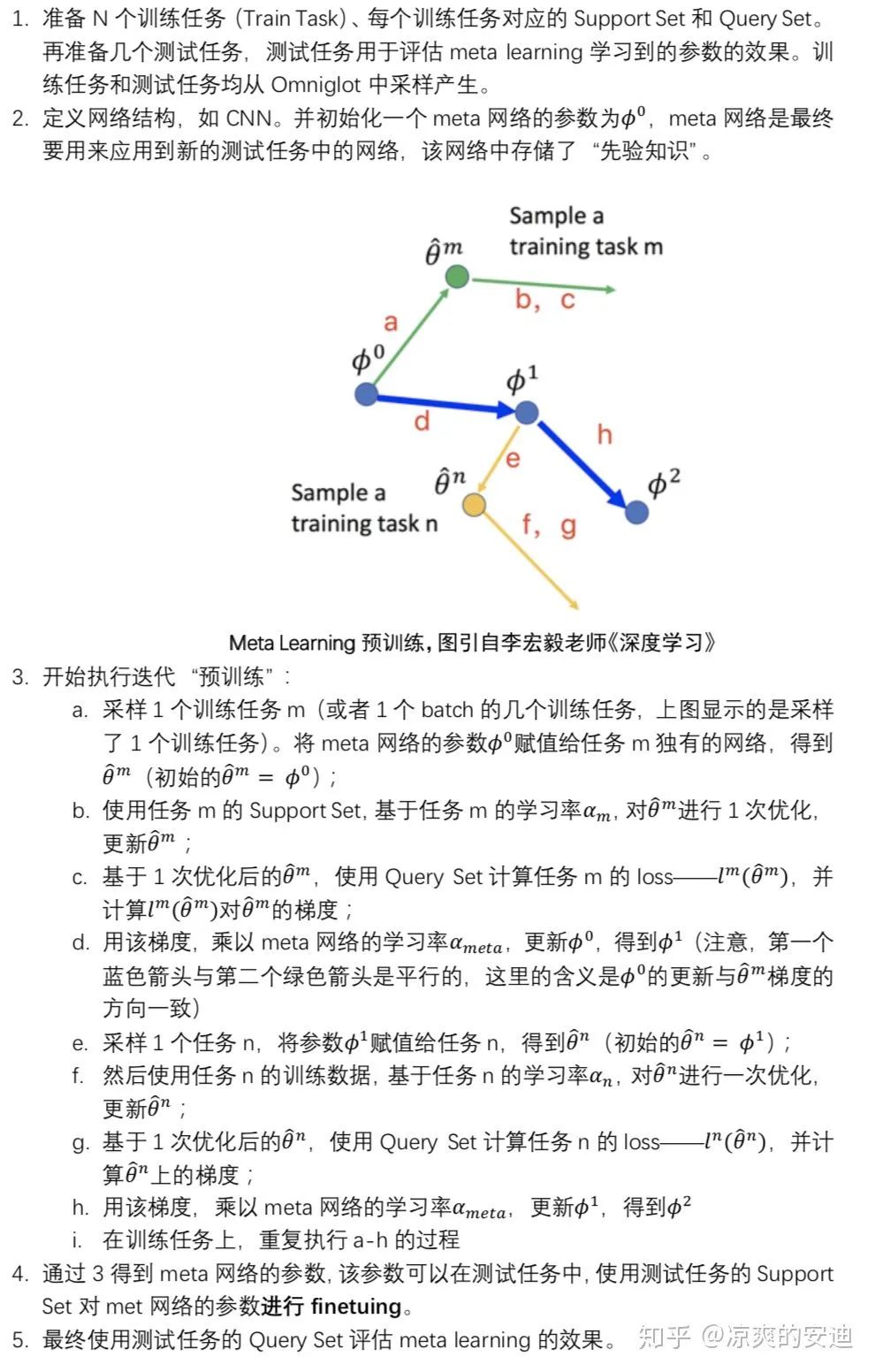
❝「当然，在“预训练”阶段，也可以sample出1个batch的几个任务，那么在更新meta网络时，要使用sample出所有任务的梯度之和。」**注意：**在MAML中，「meta网络与子任务的网络结构必须完全相同」。
❞
这里面有几个小问题：
MAML的执行过程与model pretraining & transfer learning的区别是什么？ 为何在meta网络赋值给具体训练任务（如任务m）后，要先更训练任务的参数，再计算梯度，更新meta网络？ 在更新训练任务的网络时，只走了一步，然后更新meta网络。为什么是一步，可以是多步吗？
这三个问题是MAML中很核心的问题，大家可以先思考一下，我们将在后文进行解答。我们先看一下MAML的实现代码。
## 网络构建部分: refer: https://github.com/dragen1860/MAML-TensorFlow
#################################################
# 任务描述：5-ways，1-shot图像分类任务，图像统一处理成 84 * 84 * 3 = 21168的尺寸。
# support set：5 * 1
# query set：5 * 15
# 训练取1个batch的任务：batch size：4
# 对训练任务进行训练时，更新5次：K = 5
#################################################
print(support_x) # (4, 5, 21168)
print(query_x) # (4, 75, 21168)
print(support_y) # (4, 5, 5)
print(query_y) # (4, 75, 5)
print(meta_batchsz) # 4
print(K) # 5
model = MAML()
model.build(support_x, support_y, query_x, query_y, K, meta_batchsz, mode='train')
class MAML:
def __init__(self):
pass
def build(self, support_xb, support_yb, query_xb, query_yb, K, meta_batchsz, mode='train'):
"""
:param support_xb: [4, 5, 84*84*3]
:param support_yb: [4, 5, n-way]
:param query_xb: [4, 75, 84*84*3]
:param query_yb: [4, 75, n-way]
:param K: 训练任务的网络更新步数
:param meta_batchsz: 任务数，4
"""
self.weights = self.conv_weights() # 创建或者复用网络参数；训练任务对应的网络复用meta网络的参数
training = True if mode is 'train' else False
def meta_task(input):
"""
:param support_x: [setsz, 84*84*3] (5, 21168)
:param support_y: [setsz, n-way] (5, 5)
:param query_x: [querysz, 84*84*3] (75, 21168)
:param query_y: [querysz, n-way] (75, 5)
:param training: training or not, for batch_norm
:return:
"""
support_x, support_y, query_x, query_y = input
query_preds, query_losses, query_accs = [], [], [] # 子网络更新K次，记录每一次queryset的结果
## 第0次对网络进行更新
support_pred = self.forward(support_x, self.weights, training) # 前向计算support set
support_loss = tf.nn.softmax_cross_entropy_with_logits(logits=support_pred, labels=support_y) # support set loss
support_acc = tf.contrib.metrics.accuracy(tf.argmax(tf.nn.softmax(support_pred, dim=1), axis=1),
tf.argmax(support_y, axis=1))
grads = tf.gradients(support_loss, list(self.weights.values())) # 计算support set的梯度
gvs = dict(zip(self.weights.keys(), grads))
# 使用support set的梯度计算的梯度更新参数，theta_pi = theta - alpha * grads
fast_weights = dict(zip(self.weights.keys(), \
[self.weights[key] - self.train_lr * gvs[key] for key in self.weights.keys()]))
# 使用梯度更新后的参数对quert set进行前向计算
query_pred = self.forward(query_x, fast_weights, training)
query_loss = tf.nn.softmax_cross_entropy_with_logits(logits=query_pred, labels=query_y)
query_preds.append(query_pred)
query_losses.append(query_loss)
# 第1到 K-1次对网络进行更新
for _ in range(1, K):
loss = tf.nn.softmax_cross_entropy_with_logits(logits=self.forward(support_x, fast_weights, training),
labels=support_y)
grads = tf.gradients(loss, list(fast_weights.values()))
gvs = dict(zip(fast_weights.keys(), grads))
fast_weights = dict(zip(fast_weights.keys(), [fast_weights[key] - self.train_lr * gvs[key]
for key in fast_weights.keys()]))
query_pred = self.forward(query_x, fast_weights, training)
query_loss = tf.nn.softmax_cross_entropy_with_logits(logits=query_pred, labels=query_y)
# 子网络更新K次，记录每一次queryset的结果
query_preds.append(query_pred)
query_losses.append(query_loss)
for i in range(K):
query_accs.append(tf.contrib.metrics.accuracy(tf.argmax(tf.nn.softmax(query_preds[i], dim=1), axis=1),
tf.argmax(query_y, axis=1)))
result = [support_pred, support_loss, support_acc, query_preds, query_losses, query_accs]
return result
# return: [support_pred, support_loss, support_acc, query_preds, query_losses, query_accs]
out_dtype = [tf.float32, tf.float32, tf.float32, [tf.float32] * K, [tf.float32] * K, [tf.float32] * K]
result = tf.map_fn(meta_task, elems=(support_xb, support_yb, query_xb, query_yb),
dtype=out_dtype, parallel_iterations=meta_batchsz, name='map_fn')
support_pred_tasks, support_loss_tasks, support_acc_tasks, \
query_preds_tasks, query_losses_tasks, query_accs_tasks = result
if mode is 'train':
self.support_loss = support_loss = tf.reduce_sum(support_loss_tasks) / meta_batchsz
self.query_losses = query_losses = [tf.reduce_sum(query_losses_tasks[j]) / meta_batchsz
for j in range(K)]
self.support_acc = support_acc = tf.reduce_sum(support_acc_tasks) / meta_batchsz
self.query_accs = query_accs = [tf.reduce_sum(query_accs_tasks[j]) / meta_batchsz
for j in range(K)]
# 更新meta网络，只使用了第 K步的query loss。这里应该是个超参，更新几步可以调调
optimizer = tf.train.AdamOptimizer(self.meta_lr, name='meta_optim')
gvs = optimizer.compute_gradients(self.query_losses[-1])
# def ********
接下来回答一下上面的三个问题：
「问题1：MAML的执行过程与model pretraining & transfer learning的区别是什么？」
我们将meta learning与model pretraining的loss函数写出来。
meta learning与model pretraining的loss函数
注意这两个loss函数的区别：
meta learning的L来「源于训练任务上网络的参数更新过一次后」（该网络更新过一次以后，网络的参数与meta网络的参数已经有一些区别）「，然后使用Query Set」计算的loss； model pretraining的L来源于「同一个model的参数」（只有一个），使用训练数据计算的loss和梯度对model进行更新；如果有多个训练任务，我们可以将这个参数在很多任务上进行预训练，训练的所有梯度都会直接更新到model的参数上。
看一下二者的更新过程简图：
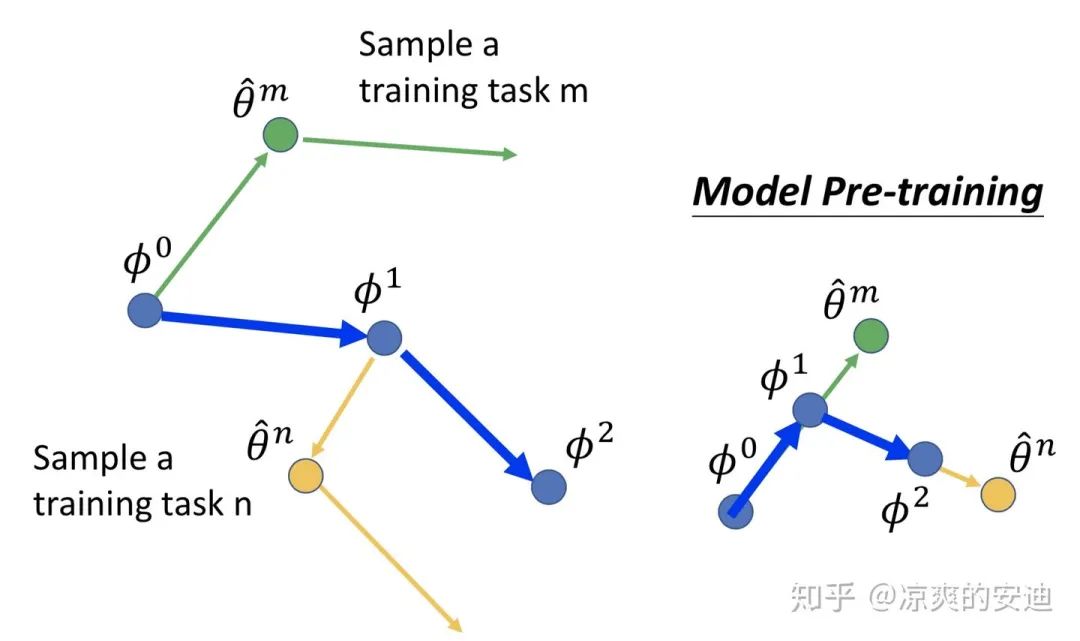meta learning与model pretraining训练过程，引自李宏毅《深度学习》
MAML是使用子任务的参数，「第二次更新」的gradient的方向来更新参数（所以左图，第一个蓝色箭头的方向与第二个绿色箭头的方向平行；左图第二个蓝色箭头的方向与第二个橘色箭头的方向平行） 而model pretraining是使用子任务第一步更新的gradient的方向来更新参数(子任务的梯度往哪个方向走，model的参数就往哪个方向走)。
从sense上直观理解：
model pretraining最小化当前的model（只有一个）在所有任务上的loss，所以model pretraining希望找到一个在所有任务（实际情况往往是大多数任务）上都表现较好的一个初始化参数，这个参数要在多数任务上「当前表现较好」。 meta learning最小化每一个子任务训练一步之后，第二次计算出的loss，用第二步的gradient更新meta网络，这代表了什么呢？子任务从【状态0】，到【状态1】，我们希望状态1的loss小，说明meta learning更care的是「初始化参数未来的潜力」。
「一个关注当下，一个关注潜力。」
如下图所示，model pretraining找到的参数 ，在两个任务上当前的表现比较好（「当下好」，但训练之后不保证好）； 而MAML的参数 在两个子任务当前的表现可能都不是很好，但是如果在两个子任务上继续训练下去，可能会达到各自任务的局部最优（「潜力好」）。
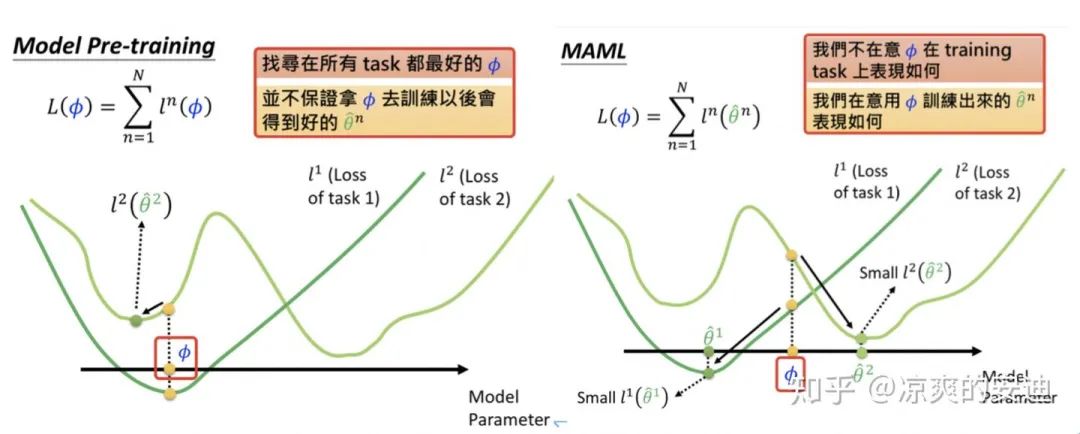
引自李宏毅《深度学习》
这里有一个toy example可以表现MAML的执行过程与model pretraining & transfer learning的区别。
训练任务：给定N个函数，y = asinx + b（通过给a和b不同的取值可以得到很多sin函数），从每个函数中sample出K个点，用sample出的K个点来预估最初的函数，即求解a和b的值。
训练过程：用这N个训练任务sample出的数据点分别通过MAML与model pretraining训练网络，得到预训练的参数。
如下图，用橘黄色的sin函数作为测试任务，三角形的点是测试任务中sample出的样本点，在测试任务中，我们希望用sample出的样本点还原橘黄色的线。
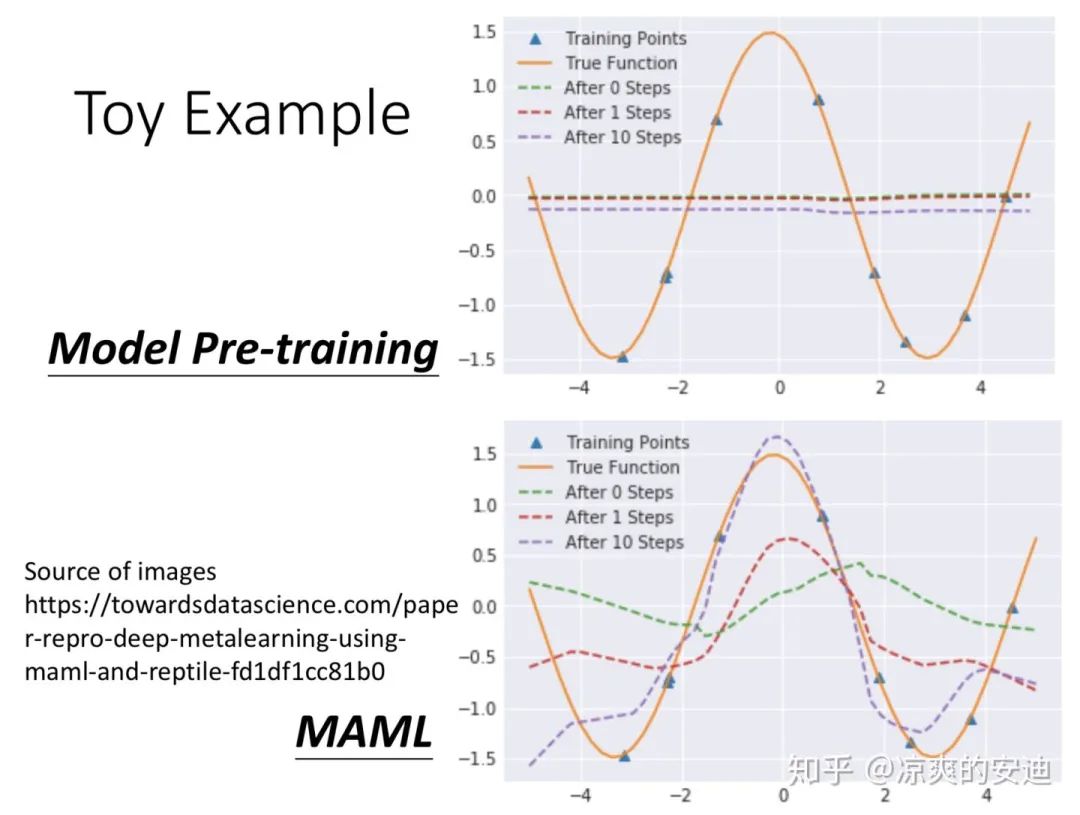
Toy example，引自李宏毅《深度学习》
model pretraining的结果，在测试任务上，在finetuning之前，绿色线是一条水平线，finetuning之后还原的线基本还是一条水平线。因为在预训练的时候，有很多sin函数，model pretraining希望找到一个在所有任务上都效果较好的初始化结果，但是许多sin函数波峰和波谷重叠起来，基本就是一条水平线。用这个初始化的结果取finetuning，得到的结果仍然是水平线。 MAML的初始化结果是绿色的线，和橘黄色的线有差异。但是随着finetuning的进行，结果与橘黄色的线更加接近。
「问题2：为何在meta网络赋值给具体训练任务（如任务m）后，要先更训练任务的参数，再计算梯度，更新meta网络？」
这个问题其实在问题1中已经进行了回答，更新一步之后，避免了meta learning陷入了和model pretraining一样的训练模式，更重要的是，可以使得meta模型更关注参数的**“潜力”**。
「问题3：在更新训练任务的网络时，只走了一步，然后更新meta网络。为什么是一步，可以是多步吗？」
李宏毅老师的课程中提到：
只更新一次，速度比较快；因为meta learning中，子任务有很多，都更新很多次，训练时间比较久。 MAML希望得到的初始化参数在新的任务中finetuning的时候效果好。如果只更新一次，就可以在新任务上获取很好的表现。把这件事情当成目标，可以使得meta网络参数训练是很好（目标与需求一致）。 当初始化参数应用到具体的任务中时，也可以finetuning很多次。 Few-shot learning往往数据较少。
那么MAML中的训练任务的网络可以更新多次后，再更新meta网络吗？
我觉得可以。直观上感觉，更新次数决定了子任务对于meta网络的影响程度，我觉得这个步数可以作为一个参数来调。
另外，即将介绍的下一个网络——Reptile，也是对训练任务网络进行多次更新的。
「3. Reptile」
Reptile与MAML有点像，我们先看一下Reptile的训练简图：
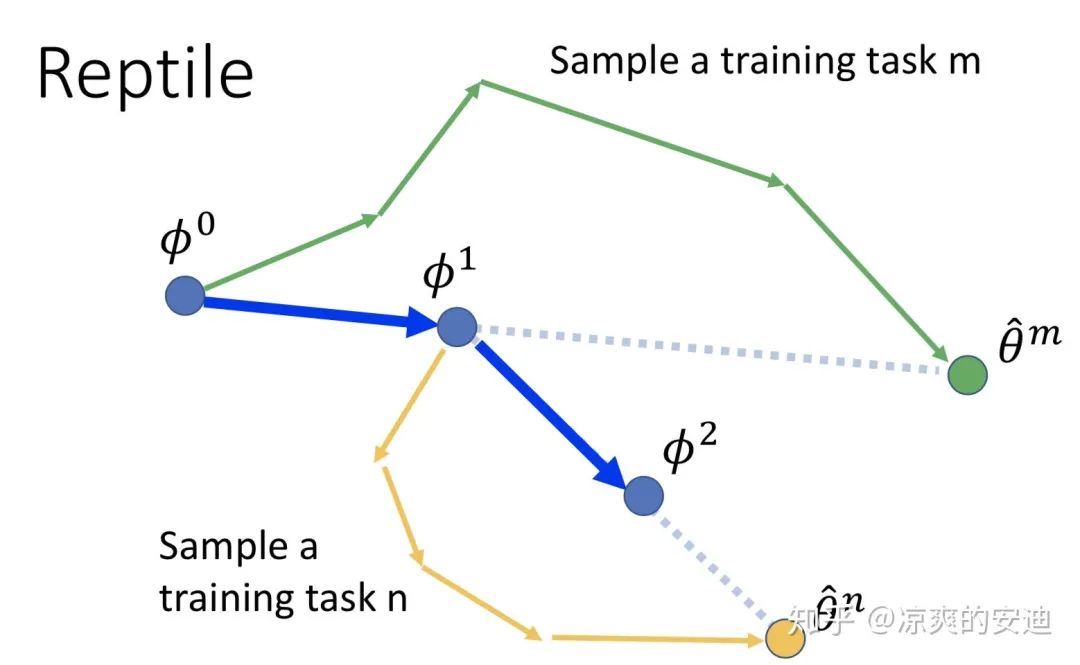Reptile训练过程，引自李宏毅《深度学习》
Reptile的训练过程如下：
Reptile，每次sample出1个训练任务
Reptile，每次sample出1个batch训练任务
在Reptile中：
训练任务的网络可以更新多次 reptile不再像MAML一样计算梯度（因此带来了工程性能的提升），而是直接用一个参数 乘以meta网络与训练任务的网络参数的差来更新meta网络参数 从效果上来看，Reptile效果与MAML基本持平
「4. What's more」
元学习入门部分的文章基本就分享到这里了~
从出发点上来看，元学习和model pretraining有点像，即，都是让网络具有一些先验知识。 从训练过程的设计来看，元学习更关注模型的潜力，而model pretraining更注重模型当下在多数情况下的表现，效果孰好孰坏很难直接判定。这大概也就是仰望天空和脚踏实地的区别hahaha 元学习除了可以初始化参数以外，还有一些设计可以帮助确定网络结构，如何更新参数等等这里有李宏毅老师的一个课程大家可以关注一下https://www.youtube.com/watch?v=c10nxBcSH14 。
分享一个关于元学习的搞笑的图。。。
老千层饼，你永远都不知道你咬下去的这一口有多少层。。
接下来可能会分享一篇MAML的数学推导，以及想把当前工作里的model pretraining模型切到meta learning看一下效果。
「最后的最后，求赞求收藏求关注~」
「参考文献」
Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks[C]//Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017: 1126-1135. Nichol A, Schulman J. Reptile: a scalable metalearning algorithm[J]. arXiv preprint arXiv:1803.02999, 2018, 2: 2. https://github.com/dragen1860/MAML-TensorFlow https://www.youtube.com/watch?v=c10nxBcSH14 [https://www.bilibili.com/video/BV1J](