鱼眼相机模型
点击下方卡片,关注“新机器视觉”公众号
视觉/图像重磅干货,第一时间送达

鱼眼镜头
之前的文章我们介绍了针孔相机模型,相机镜头是一个凸透镜,而本文介绍的鱼眼相机镜头是由十几个不同的透镜组合而成,在成像的过程中,入射光线经过不同程度的折射,投影到尺寸有限的成像平面上,使得鱼眼镜头拥有更大的视野范围。下图为鱼眼相机的组成结构:
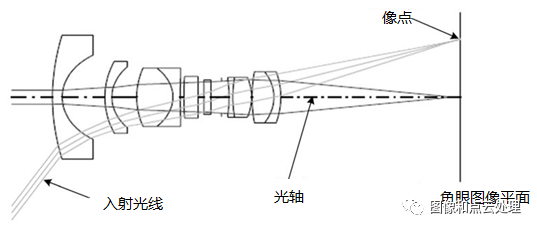
与针孔相机原理不同,鱼眼镜头采用非相似成像,在成像过程中引入畸变,通过对直径空间的压缩,突破成像视角的局限,从而达到广角成像。
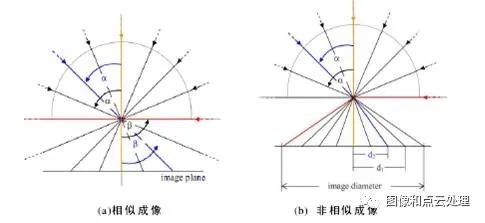
所以鱼眼镜头是一种极端的广角镜头,通常焦距小于等于16mm并且视角接近或等于180°(在工程上视角超过140°的镜头即统称为鱼眼镜头)。
相机畸变
鱼眼镜头无论如何它的边缘线条都是要弯曲的,即使90度的鱼眼也是这样,这种畸变我们在很多广角镜头上都可以看到,而这就是明显的桶形畸变。同样的120度的鱼眼看起来弯曲的更加厉害一些了,而且被容纳进范围的景物更多;150度同样如此,而180度的鱼眼则可以把镜头周围180度范围内的所有物体都拍摄进去。众所周知,焦距越短,视角越大,因光学原理产生的变形也就越强烈。为了达到180度的超大视角,鱼眼镜头不得不允许这种变形(桶形畸变)的合理存在。
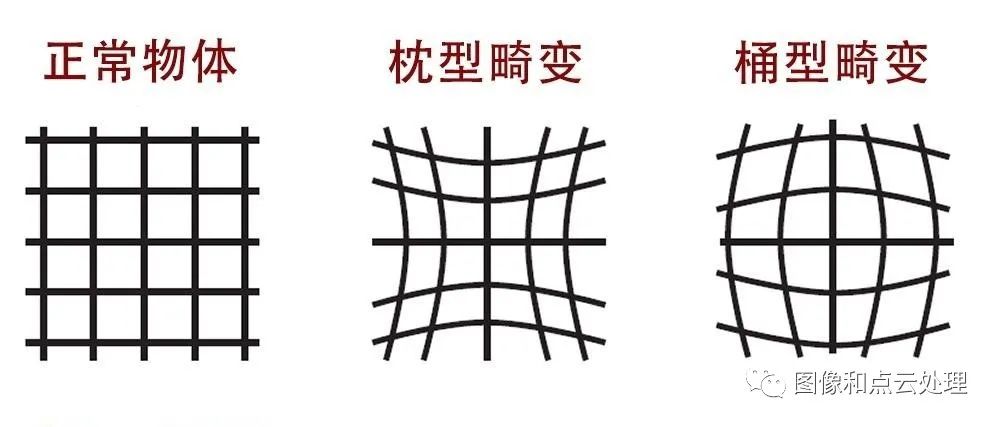
针对原始图像进行畸变校正后,带有冗余边界,需要做进一步截取。如下图:

投影模型
通常的光学系统均基于高斯光学,遵循相似成像准则,而鱼眼镜头为了将尽可能大的场景投影到有限的图像平面内采用非相似成像,故需要选择其他的成像公式来替换高斯光学成像公式,每一个成像公式对应一种镜头设计模型。常用的鱼眼镜头模型一共有四个,分别是等距投影、正交投影、等立体角投影、体视投影。
f为鱼眼相机的焦距,即成像平面的半径,θ是入射光线与鱼眼相机光轴的夹角,即入射角,rd为鱼眼图像的点到畸变中心的距离。rd随着设计模型的变化而发生变化,四种模型投射距离的大小关系如下(反映空间中的一点P投影到球面再到图像平面的成像过程):
等距投影的成像点的位置rd与入射角θ成正比。这种模型可以解决在小孔成像下入射角为 90°时图像无限拉伸的问题,在二维图像中,成像为随着入射角不断变化的同心圆,最大视场角可达到 360°,这种鱼眼模型是最简单的一种模型。
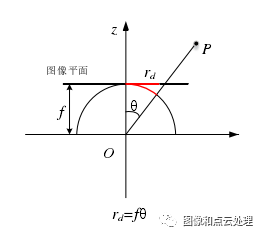
正交投影的成像结果,不会产生出透射映射的近大远小结果。在二维图像中,从 0 到 90 度,等差的视场角成像越来越密。180度视场角以内的场景都可以进行投影。
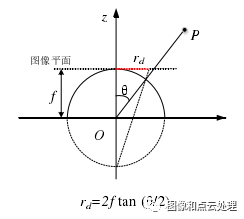
等立体角投影是鱼眼镜头中比较常用的一种模型。
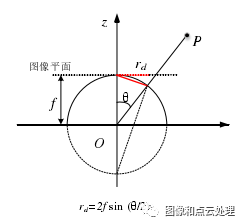
体视投影是一种将圆球投影至平面的映射,在几何学里也称共型映射,是一种保角映射。此时相机的光心移至南极的位置,光轴朝北极。体视投影可以将 360度的场景都投影到图像上。

成像模型
相比针孔相机模型可以将三维点直接投影到归一化平面,鱼眼相机则多了一个中间过程:先将三维点投影到单位球面,再将单位球面上的点投影到归一化平面上。
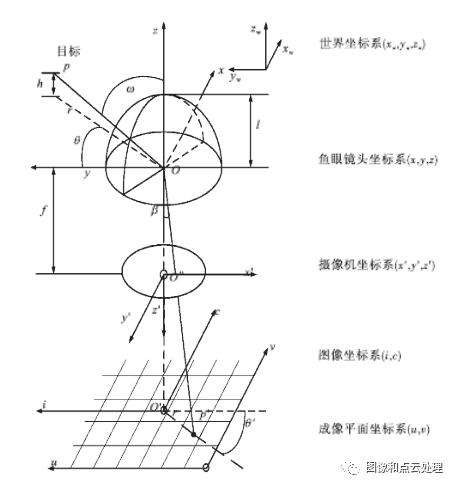
对于三维世界中的一点𝑃,其坐标向量为𝑋,𝑃在相机坐标系中的坐标Xc = RX + T。其中R、T分别为世界坐标系到相机坐标系的旋转与平移矩阵,对于针孔投影到相平面上的坐标(𝑎, 𝑏),满足如下等式:

其中:
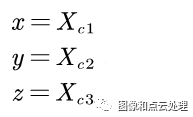
加入鱼眼相机畸变:
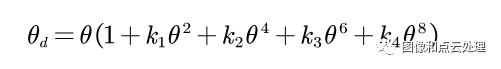
畸变后坐标(𝑥′, 𝑦′),满足:
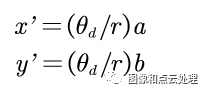
最后调整到像素坐标系(𝑢, 𝑣):
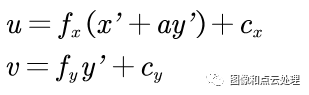
其中𝑓𝑥= f/d𝑥, 𝑓𝑦= f/d𝑦分别为两个方向上的归一化焦距,d𝑥, d𝑦代表了一个像素点对应的图像平面中的长度。
本文来自杨旭童鞋的整理,在此感谢!
