逻辑面试题：1+1=2最复杂的打开方式
苦逼的码农
共 6707字，需浏览 14分钟
·
2021-06-17 20:38
教授在每个人脑门上贴了一张纸条
每个人的纸条上都写了一个正整数，且某两个数的和等于第三个数
每个人可以看见另两个数，但看不见自己的
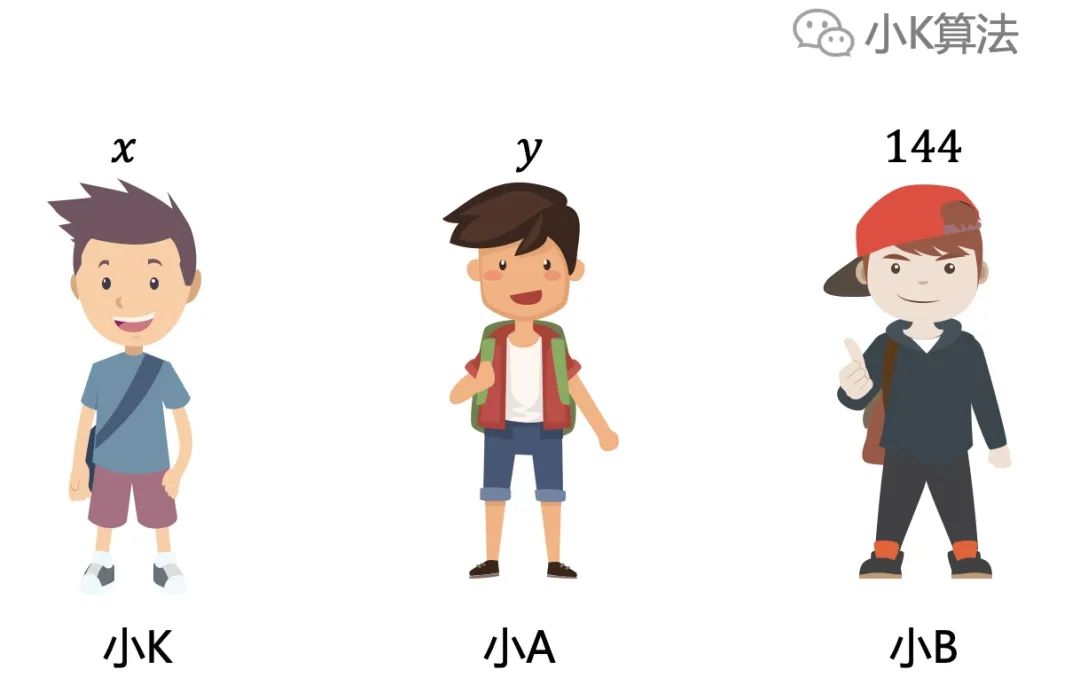
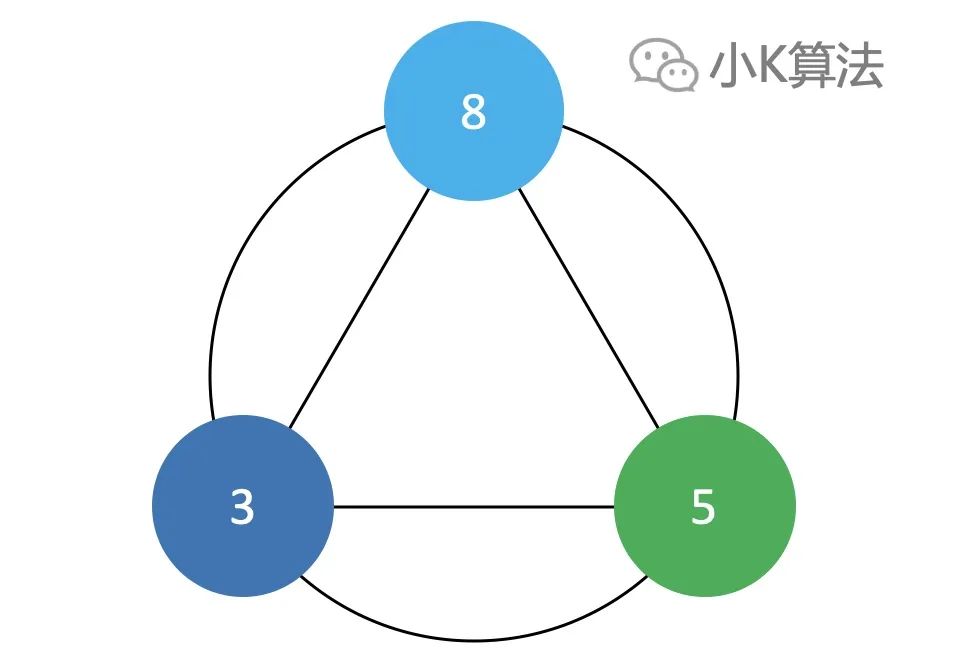
每个人自己的数只能是另两数之和或者之差，所以每个人都有2种可能。
每个人都无法确认自己到底是哪一个，也不能从其他人那里得到更多信息。
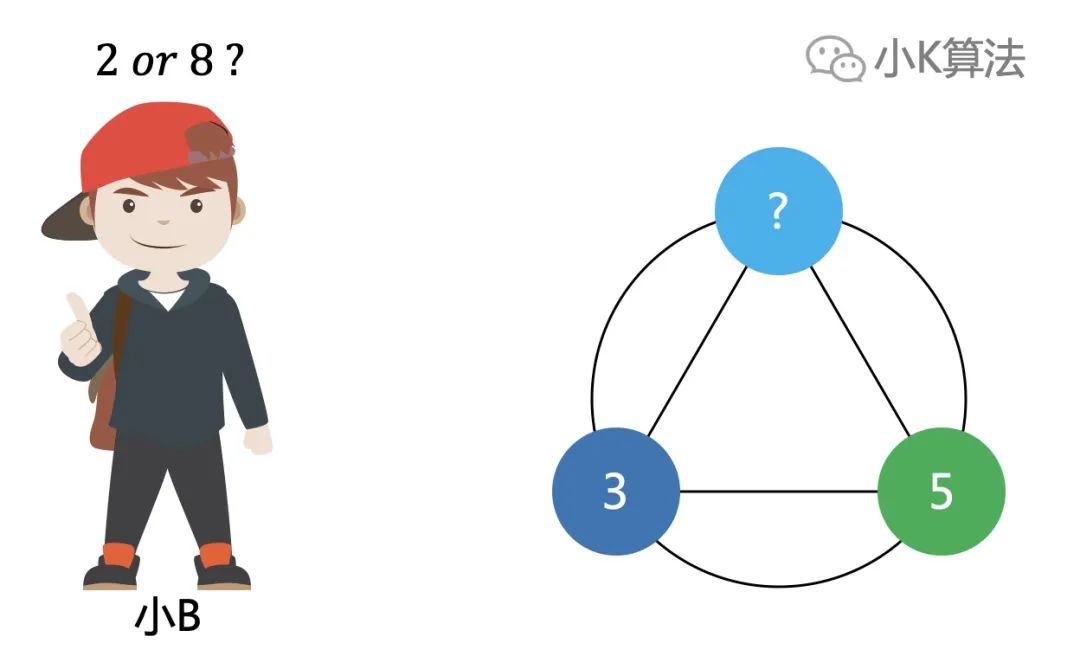
再回到问题描述，“每个人的纸条上都写了一个正整数”，这就是最关键的信息，它暗示了很多其它信息。如果有一个人计算出来的数不是正整数，那这一种情况就被排除。
这个数不可能是负数，因为2个不相等的数，一定是用大的减去小的，那剩下的非正整数就只能是0，也就是有2个数相等的情况。
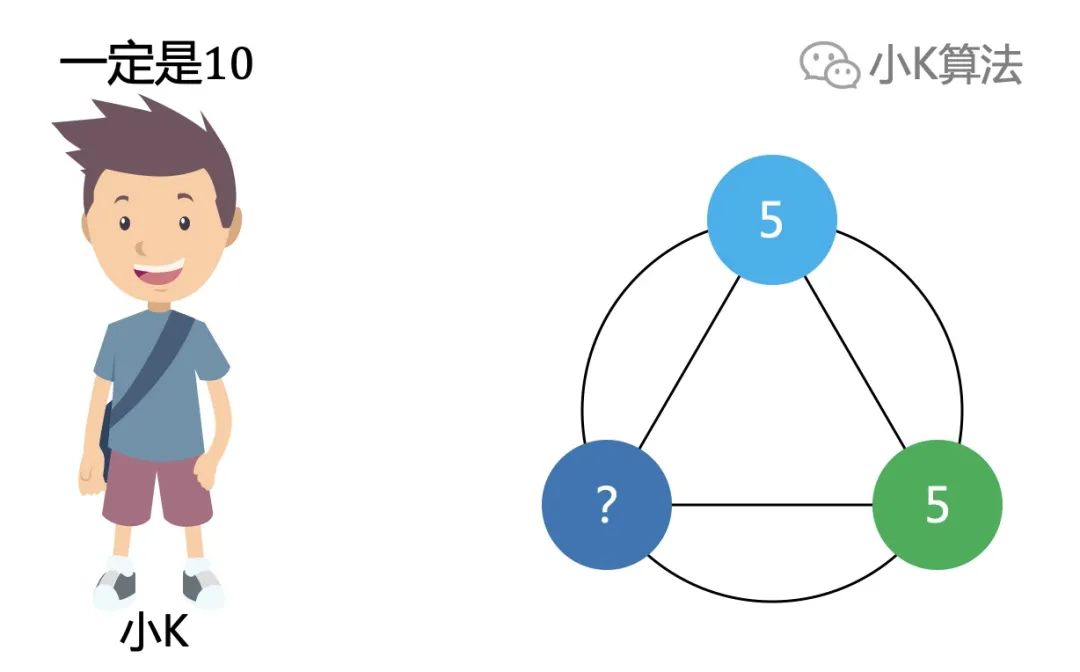
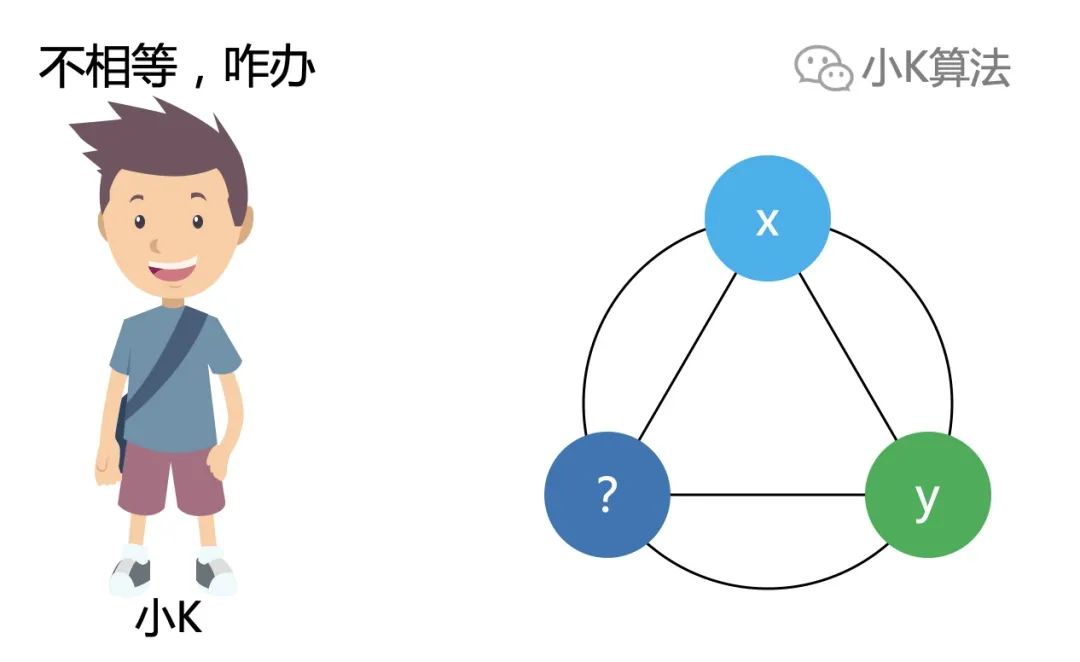
如果2个数相等，抽象一下，不就是一个最简单的1+1=2的问题吗？
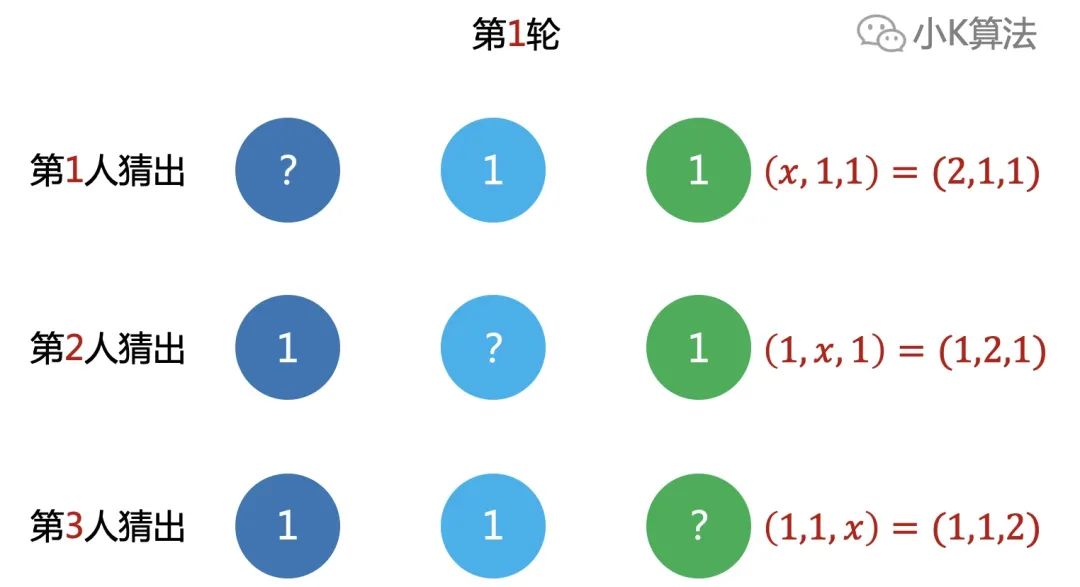
如果小A看到的场景刚好是这样，(2,y,1)，那y不是1，肯定就是3了呀。
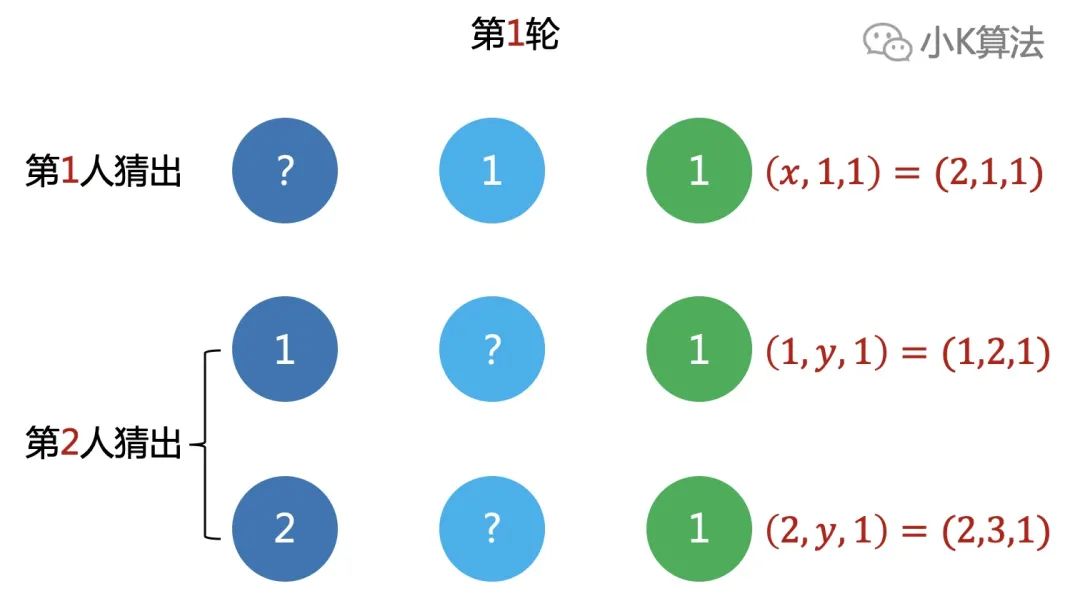
第2轮第1人能猜出的情况如下：
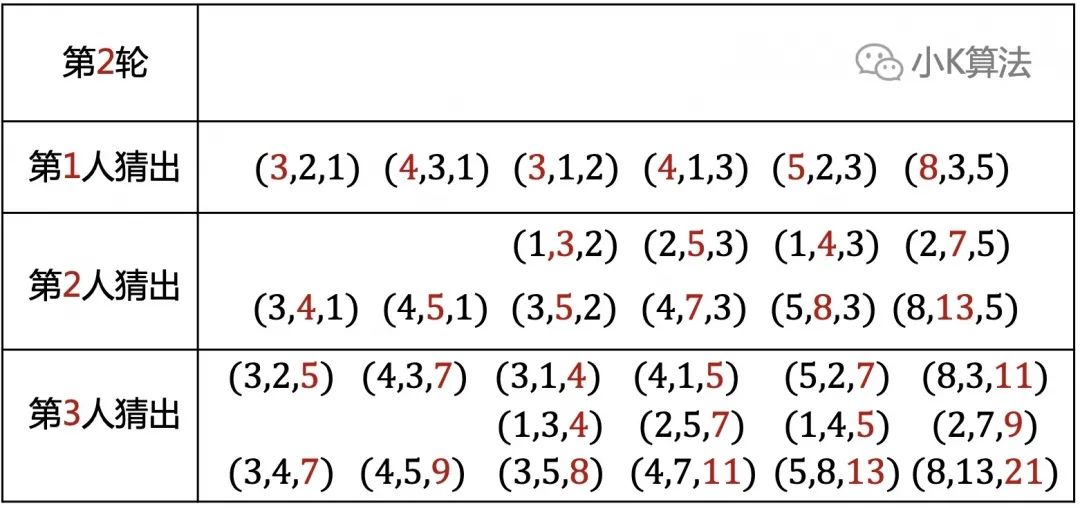
正确的解有5个：(3,1,4)，(1,3,4)，(2,7,9)，(4,5,9)，(3,5,8)。
对应的另外两个数分别是：(108,36)，(36,108)，(32,112)，(64,80)，(54,90)。
3个数要先约掉公约数，等比例的情况都是相同的
任意情况，都会在有限轮次之后被某个人猜出来
最先猜出来的人，一定是数字最大的人
所有逻辑推理的根基都是1+1=2 每多一轮，解的个数以斐波那契数列递增
struct Node {
int x, y, z, level;
};
Node f[10000];
int last1, last2, tail;
void init() {
f[0] = Node{2, 1, 1, 1};
f[1] = Node{1, 2, 1, 2};
f[2] = Node{2, 3, 1, 2};
f[3] = Node{1, 1, 2, 3};
f[4] = Node{2, 1, 3, 3};
f[5] = Node{1, 2, 3, 3};
f[6] = Node{2, 3, 5, 3};
last1 = 3;
last2 = 1;
tail = 7;
}
// 第round轮，第person人，猜出自己是x
void solve(int round, int person, int x) {
int n = (round - 2) * 3 + person, total;
for (int i = 0; i < n; ++i) {
total = tail;
for (int j = last2; j < total; ++j) {
if (i % 3 == 0) {
f[tail++] = Node{f[j].y + f[j].z, f[j].y, f[j].z, 4 + i};
} else if (i % 3 == 1) {
f[tail++] = Node{f[j].x, f[j].x + f[j].z, f[j].z, 4 + i};
} else {
f[tail++] = Node{f[j].x, f[j].y, f[j].x + f[j].y, 4 + i};
}
}
last2 = last1;
last1 = total;
}
for (int i = last1; i < tail; ++i) {
int temp = 0;
switch (person) {
case 1:
temp = f[i].x;
break;
case 2:
temp = f[i].y;
break;
case 3:
temp = f[i].z;
break;
}
if (x % temp == 0) {
int s = x / f[i].z;
printf("(%d, %d, %d), level=%d\n", f[i].x * s, f[i].y * s, f[i].z * s, f[i].level);
}
}
}
int main() {
init();
solve(2, 3, 144);
return 0;
}
(108, 36, 144), level=6
(36, 108, 144), level=6
(32, 112, 144), level=6
(64, 80, 144), level=6
(54, 90, 144), level=6
评论