清华大学马少平老师教AI:第一篇 神经网络是如何实现的(一)

第一篇 神经网络是如何实现的(一)
清华大学计算机系 马少平
前言
近些年来,人工智能发展很快,再一次掀起了高潮,逐渐渗透到各行各业、各个领域,学习人工智能相关技术的人也越来越多,市面上也出现了很多非常出色的相关书籍。但也经常听到一些朋友抱怨,说这些书太专业了,读起来比较费劲。为此,我利用各种机会写过一些科普文章,介绍人工智能相关的内容,也做过一些科普报告。但也有朋友反馈说,这些科普内容虽然听懂了,但是还是不知道如何实现的,能不能有一本既通俗易懂、又能帮助我们了解具体技术的书,让我们比较容易看懂人工智能究竟是如何实现的。
为此,我思考了很长时间,想写一本能满足这些朋友要求的书。但是几次动笔,都中途而废,写不下去了。这里的关键是如何定位问题。经过很多业内人士、包括我们组内的同学等,在这个过程中给了我很多鼓励和很好的建议,最终我想尝试着写一本有关人工智能入门的初级读物,读者对象定位在具有一定的理工科背景的朋友,用通俗易懂的语言,由浅入深,讲授人工智能的基本原理。在写的过程中,我想到了“一师一生”的具有一定交互的写作方法,书中设计了“艾博士”这样一位博学的老师(“艾”即AI),和一位聪明好学的学生小明,通过二人的对答,讲授人工智能的基本原理和方法。
《计算机是如何实现智能的》计划共由六篇内容组成,每篇内容独立成章。除了文字内容外,每篇内容还配有若干个讲解视频,每段视频在20分钟左右,以利于朋友们学习。
本书作为人工智能的入门性通俗读本,将引领您走进人工智能的世界。
这里推出的是本书的第一篇:神经网络是如何实现的。
这是我们的初步尝试,效果如何,还请朋友们多加赐教。欢迎各位朋友留下您宝贵的意见和建议,对于书中出现的任何不当之处或没有说明白的地方,还望不吝赐教,本人将不胜感激。
艾博士导读
这些年人工智能蓬勃发展,在语音识别、图像识别、自然语言处理等多个领域得到了很好的应用。推动这波人工智能浪潮的无疑是深度学习。所谓的深度学习实际上就是多层神经网络,至少到目前为止,深度学习基本上是用神经网络实现的。神经网络并不是什么新的概念,早在上个世纪40年代就开展了以感知机为代表的神经网络的研究,只是限于当时的客观条件,提出的模型比较简单,只有输入、输出两层,功能有限,连最简单的异或问题(XOR问题)都不能求解,神经网络的研究走向低潮。
到了80年代中期,随着BP算法的提出,神经网络再次引起研究热潮。当时被广泛使用的神经网络,在输入层和输出层之间引入了隐含层,不但能轻松求解异或问题,还被证明可以逼近任意连续函数。但限于计算能力和数据资源的不足,神经网络的研究再次陷入低潮。
一直对神经网络情有独钟的多伦多大学的辛顿教授,于2006年在《科学》上发表了一篇论文,提出了深度学习的概念,至此神经网络以深度学习的面貌再次出现在研究者的面前。但是深度学习并不是简单地重复以往的神经网络,而是针对以往神经网络研究中存在的问题,提出了一些解决方法,可以实现更深层次的神经网络,这也是深度学习一词的来源。
随着深度学习方法先后被应用到语音识别、图像识别中,并取得了传统方法不可比拟的性能,深度学习引起了人工智能研究的再次高潮。
那么神经网络是如何实现的呢?本篇将逐一解开这个谜团。
本篇内容按照难易程度划分为三个等级,读者可以根据自身需要有选择的读其中几节或者全部内容。
第一级:1.1节到1.2节,介绍神经元和神经网络的基本概念。通过一个简单的数字识别问题,引出神经元的概念,以及神经元与模式之间的对应关系。然后系统地介绍了神经元和全连接神经网络。
第二级:1.3节到1.4节,介绍神经网络的基本训练方法,引出BP算法以及BP算法的基本工作原理。从模式提取的角度引出卷积神经网络的概念,并进一步讲解卷积神经网络的实现方法。最后介绍了几个神经网络的应用实例,详细说明其组成结构等。在阅读这些内容之前,需要读者大体了解向量、导数、偏导数等基本概念,但并不需要太深的知识。
第三级:1.5节到1.11节,介绍什么是梯度消失问题以及常用的解决方法。介绍什么是过拟合问题以及常用的解决方法。为了用神经网络处理自然语言问题,引出词的表示方法及求解方法。对于像语句这样的序列数据处理对象,介绍了什么是循环神经网络以及求解方法,给出了一些应用实例。接下来介绍了一种特殊的循环神经网络LSTM,讲解了其组成结构和基本的求解原理。同第二级一样,需要读者大体了解向量、导数、偏导数等基本概念,但并不需要太深的知识。
小明是个聪明好学的孩子,对什么事情都充满了好奇心。最近人工智能火热,无论是电视上,还是网络媒体上,经常听到的一个词就是神经网络。小明在生物课上学习过人类的神经网络,我们的思维思考过程,都是依赖于大脑的神经网络而进行的。那么计算机上的神经网络是如何实现的呢?带着这个问题,小明找到了万能的艾博士,向艾博士请教有关神经网络的实现原理以及计算机是如何利用神经网络实现一些智能功能的。
第一节:从数字识别谈起
这天是周末,艾博士正在家中整理自己的读书笔记,为周一的讲课做准备,在得知了小明的来意之后,对小明说:小明,你来的刚好,我正在准备这方面的资料,我们一起来探讨一下这个问题。
小明你看,图1.1(a)是个数字3的图像,其中1代表有笔画的部分,0代表没有笔画的部分。假设想对0到9这十个数字图像进行识别,也就是说,如果任给一个数字图像,我们想让计算机识别出这个图像是数字几,我们应该如何做呢?
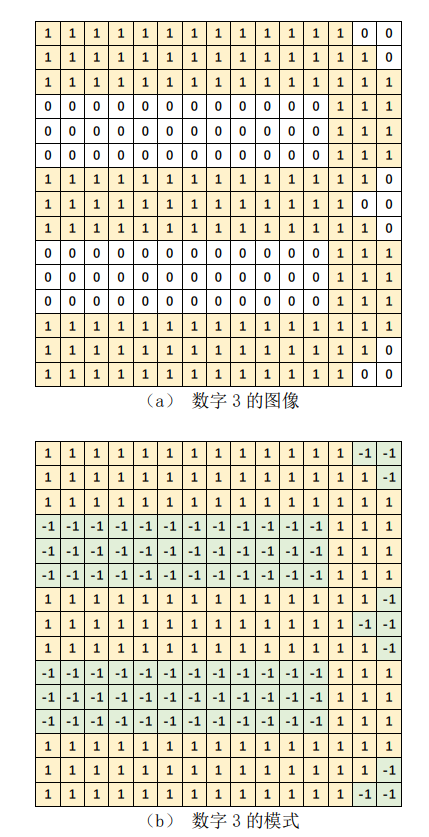
图1.1 数字3的图像和模式
一种简单的办法就是对每个数字构造一个模式,比如对数字3,我们这样构造模式:有笔画的部分用1表示,而没有笔画的部分,用-1表示,如图1.1(b)所示。当有一个待识别图像时,我们用待识别图像与该模式进行匹配,匹配的方法就是用图像和模式的对应位置数字相乘,然后再对相乘结果进行累加,累加的结果称为匹配值。为了方便表示,我们将模式一行一行展开用
艾博士问小明:你看这样的匹配会是什么结果呢?
小明想了一下回答道:如果模式与待识别图像中的笔画是一样的,就会得到一个比较大的匹配结果,如果有不一致的地方,比如模式中某个位置没有笔画,这部分在模式中为-1,而待识别图像中相应位置有笔画,这部分在待识别图像中为1,这样对应位置相乘就是-1,相当于对结果做了惩罚,会使得匹配结果变小。所以我猜想,匹配结果越大说明待识别图像与模式越一致,否则差别就比较大。
听了小明的回答,艾博士很高兴:小明,你说的很对。我们用3和8举例说明。如图1.2所示是8的图像。这两个数字的区别只是在最左边是否有笔画,当用8与3的模式匹配时,8的左边部分与3的模式的左边部分相乘时,会得到负值,这样匹配结果受到了惩罚,降低了匹配值。相反如果当3与8的模式匹配时,由于3的左边没有笔画值为0,与8的左边对应位置相乘得到的结果是0,也同样受到了惩罚,降低了匹配值。只有当待识别图像与模式笔画一致时,才会得到最大的匹配值。
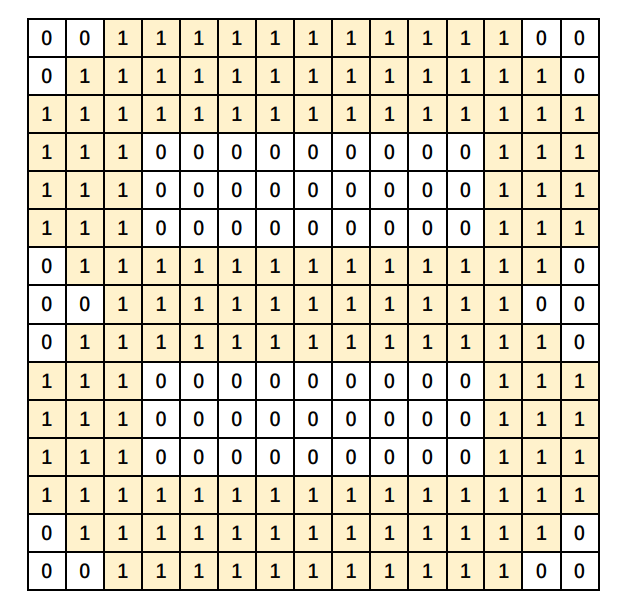
图1.2 数字8的图像
接着,艾博士让小明算一下数字3、8分别与3的模式的匹配值各是多少。小明很快就给出了计算结果,3与3的模式的匹配值是143,而8与3的模式的匹配值是115。可见前者远大于后者。图1.3给出了数字8与模式3匹配的示意图,为表示方便用了一个小图。
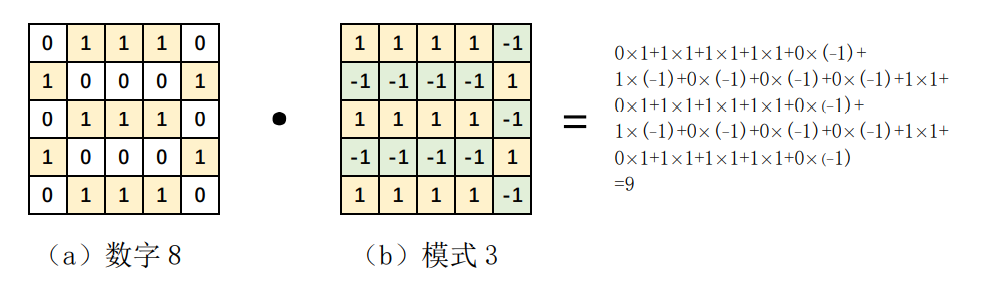
图1.3 数字8与模式3的对应位置相乘再累加
看着计算结果小明很是兴奋,马上问艾博士:如果我想识别一个数字是3还是8,是不是分别和这两个数字的模式进行匹配,看与哪个模式的匹配值大,就是哪个数字?
艾博士肯定地回答说:非常正确。如果识别0到9这10个数字,只要分别建造这10个数字的模式就可以了。对于一个待识别图像,分别与10个模式匹配,选取匹配值最大的作为识别结果就可以了。但是由于不同数字的笔画有多有少,比如1笔画就少,而8就比较多,所以识别结果的匹配值也会有大有小,为此我们可以对匹配值用一个称作sigmoid的函数进行变换,将匹配值变换到0和1之间。sigmoid函数如下式所示,通常用
其图形如下:
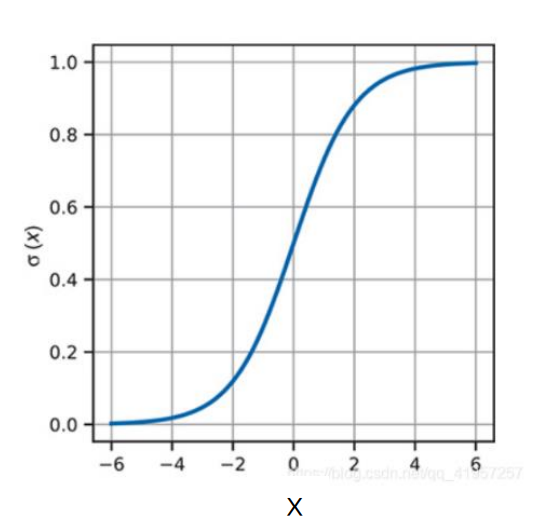
图1.4 sigmoid函数示意图
从图中可以看出,当x比较大时,sigmoid输出接近于1,而x比较小时(负数),sigmoid输出接近于0。经过sigmoid函数变换后的结果可以认作是待识别图像属于该数字的概率。
听艾博士讲到这里,聪明的小明用计算器计算一番后,马上想到一个问题:艾博士,像前面的3和8的匹配结果分别为143、115,把两个结果带入到sigmoid函数中,都接近于1了,并没有明显的区分啊?
艾博士夸赞小明想的仔细:小明说的非常对,sigmoid函数并不能直接这样用,而是要“平移”一下,加上一个适当的偏置b,使得加上偏置后,两个结果分别在sigmoid函数中心线的两边,来解决这个问题:
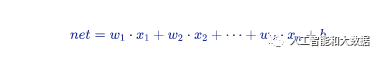
比如这里我们让b=-14,小明你再计算一下这样处理后的sigmoid值分别是多少?
小明用计算器再次计算一番后,得出结果分别是:
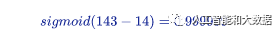
小明对这个结果非常满意:这个sigmoid函数真是神奇,这样区分的就非常清楚了,接近1的就是识别结果,而接近0的就不是。但是艾博士,对于不同的数字模式这个偏置b是固定值吗?
艾博士回答说:当然不能是固定的,不同的数字模式具有不同的b值,这样才能解决前面提到的不同数字之间笔画有多有少的问题。
经过艾博士的详细讲解,小明明白了这样一种简单的数字识别基本原理。但是,这与神经网络有什么关系呢?
对于小明的问题,艾博士在纸上画了一个示意图如图1.5所示。艾博士指着图说:我们上面介绍的,其实就是一个简单的神经网络。这是一个可以识别3和8的神经网络,和前面介绍的一样,
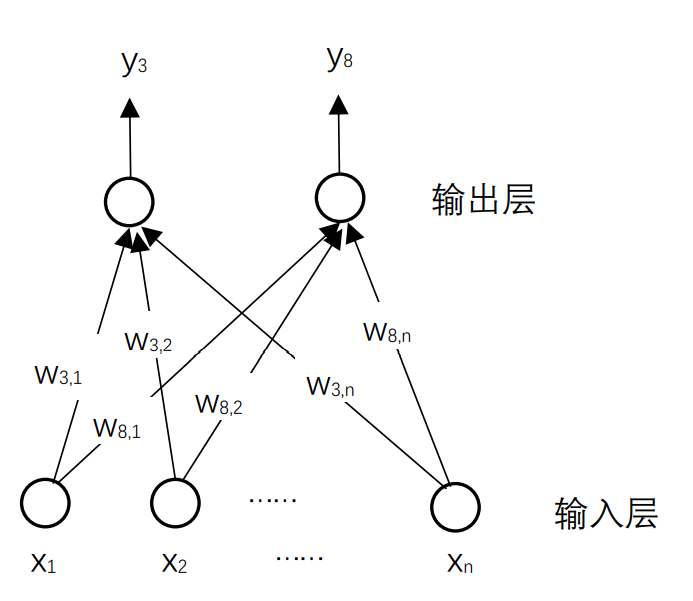
图1.5 用神经网络形式表达的数字识别
艾博士指着图进一步解释说:图中下边表示输入层,每个圆圈对应输入图像在位置
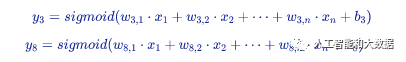
小明你看,这是不是就是我们前面讲的数字识别方法?
小明听了艾博士的解释后,恍然大悟,问道:那么是不是说每个神经元对应的权重都代表了一种模式呢?比如在这个图中,一个神经元代表的是数字3的模式,另一个神经元代表的是数字8的模式。进一步如果在输出层补足了10个数字,是不是就可以实现数字识别了?
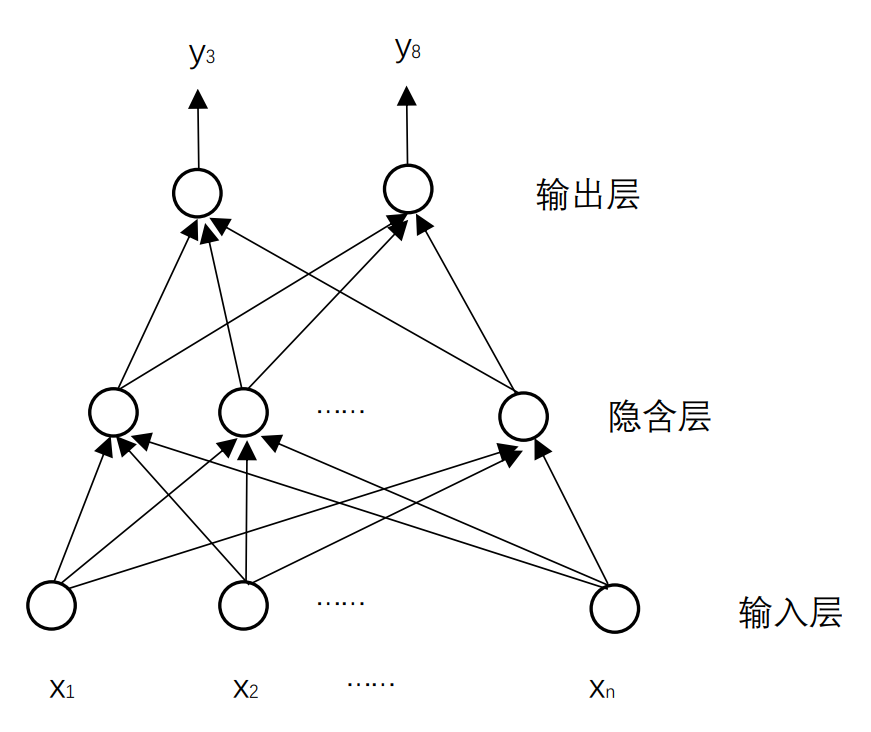
图1.6 具有一个隐含层的神经网络
在得到了艾博士的肯定回答后,小明又问道:刚刚您说这是一个简单的神经网络,那么是否有更复杂的神经网络呢?复杂的神经网络又是如何构造的呢?
艾博士回答说:这个网络过于简单了,要想构造复杂一些的网络,可以有两个途径。比如一个数字可以有不同的写法,这样的话,同一个数字就可以构造多个不同的模式,只要匹配上一个模式,就可以认为是这个数字。这是一种横向的扩展。另外一个途径就是构造局部的模式。比如可以将一个数字划分为上下左右4个部分,每个部分是一个模式,多个模式组合在一起合成一个数字。不同的数字,也可以共享相同的局部模式。比如3和8在右上、右下部分模式可以是相同的,而区别在左上和左下的模式上。要实现这样的功能,需要在神经网络的输入层、输出层之间增加一层表示局部模式的神经元,这层神经元由于在神经网络的中间部分,所以被称为隐含层。如图1.6所示,输入层到隐含层的神经元之间都有带权重的连接,而隐含层到输出层之间也同样具有带权重的连接。隐含层的每个神经元,均表示了某种局部模式。这是一种纵向的扩展。
小明对照着艾博士画的图,思考了一下说:如果要刻画更细致的局部模式,是不是增加更多的隐含层就可以了?
艾博士回答说:小明说的很对,可以通过增加隐含层的数量来刻画更细致的模式,每增加一层隐含层,模式就被刻画的更详细一些。这样就建立了一个深层的神经网络,越靠近输入层的神经元,刻画的模式越细致,体现的越是细微信息的特征;越是靠近输出层的神经元,刻画的模式越是体现了整体信息的特征。这样通过不同层次的神经元体现的是不同粒度的特征。每一层隐含层也可以横向扩展,在同一层中每增加一个神经元,就增加了一种与同层神经元相同粒度特征的模式。
小明又问道:这样看起来,神经网络越深越能刻画不同粒度特征的模式,而横向神经元越多,则越能表示不同的模式。但是当神经网络变得复杂后,所要表达的模式会非常多,如何构造各种不同粒度的模式呢?
艾博士很是欣赏小明善于思考的作风:小明你这个问题非常好,上面咱们只是举例说明可以这么做。构造模式是非常难的事情,事实上我们也很难手工构造这些模式。在后面我们可以看到,这些模式,也就是神经网络的权重是可以通过样本训练得到的,也就是根据标注好的样本,神经网络会自动学习这些权值,也就是模式,从而实现数字识别。
最后艾博士总结到:通过上述讲解,我们了解了神经元可以表示某种模式,不同层次的神经元可以表示不同粒度的特征,从输入层开始,越往上表示的特征粒度越大,从开始的细粒度特征,到中间层次的中粒度特征,再到最上层的全局特征,利用这些特征就可以实现对数字的识别。如果网络足够复杂,神经网络不仅可以实现数字识别,还可以实现更多的智能系统,比如人脸识别、图像识别、语音识别、机器翻译等。
小明读书笔记
神经元实际上是模式的表达,不同的权重体现了不同的模式。权重与输入的加权和,即权重与对应的输入相乘再求和,实现的是一次输入与模式的匹配。该匹配结果可以通过sigmoid函数转换为匹配上的概率。概率值越大说明匹配度越高。
一个神经网络可以由多层神经元构成,每个神经元表达了一种模式,越是靠近输入层的神经元表达的越是细粒度的特征,越是靠近输出层的神经元表达的越是粗粒度特征。同一层神经元越多,说明表达的相同粒度的模式越多,而神经网络层数越多,越能刻画不同粒度的特征。
未完待续
