Python算法-大O表示法-技术圈

1、概念与举例

概念

大O表示法是一种特殊的表示法，它表示算法的时间复杂度（即速度）。说明：大O表示法是对算法性能的一种粗略估计，并不能精准地反映某个算法的性能。

举例

看到这里，大家可能存在疑惑，大O表示法是怎么表示的？接下来我们用一个程序介绍大O表示法是怎样表示该程序的时间复杂度（请读者用函数的角度思考以下讲解内容）。

实例1.2 计算a、b、c的值

例如：a+b+c=1000且a2+b2=c2（a、b、c都是自然数），求a、b、c的可能组合（a、b、c的范围在0~1000之间）。代码如下：

              
                for a in range(0,1000):                                                  # 遍历a
              
              
                
                  

              
              
                    for b in range(0,1000):                                           # 遍历b
              
              
                
                  

              
              
                        for c in range(0,1000):                                     # 遍历c
              
              
                
                  

              
              
                            if a+b+c==1000 and a**2 + b**2 == c**2:      # 条件
              
              
                
                  

              
              
                                print("a, b, c:",a,b,c)                          # 输出结果

最终需要大约4分钟（不同计算机的运行时间不同）之后才能运行出结果，结果如图10所示。

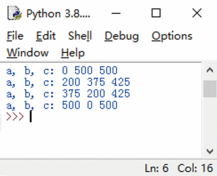
图10 运行结果

将这段代码的第03~04行进行如下修改：

              
                for a in range(0,1000):                      # 遍历a
              
              
                
                  

              
              
                    for b in range(0,1000):               # 遍历b
              
              
                
                  

              
              
                        c=1000-a-b                      # 用表达式求解c
              
              
                
                  

              
              
                        if a ** 2 + b ** 2 == c ** 2: # 条件
              
              
                
                  

              
              
                            print("a, b, c:", a, b, c)   # 输出结果

第二段代码最终运行的结果所需的时间不到1分钟，结果依然是图1.10所示的内容。从速度上看，第二段代码更快，也就是说，第二段代码算法要比第一段代码算法更成熟，意义上更好一些。那接下来从时间上分析一下这两段代码：（1）第一段代码的时间复杂度：设时间为f，这段代码用到了3个for循环，每个循环遍历一次运行的时间复杂度是1000，3次嵌套for循环的时间复杂度是每层for循环时间复杂度相乘，即T=1000*1000*1000。而for循环之后的if和print()两条语句，我们暂且算成是2。因此这段程序的时间复杂度是：

如果将for循环的范围写成0~n，那么时间复杂度就变成了一个函数，其中n是一个变量，可以写成如下形式，也等价于f(n)=n3*2：

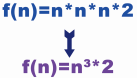
f(n)=n3*2函数在象限图的分布如图11所示。

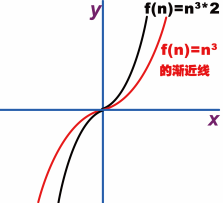
图11 立方象限图

从图像可以看到，这个函数的走势如图1.13所示，走势是不变的，而系数无论是2还是10，只不过是使这个走势更陡峭一些，并不影响大趋势，因此可以忽略系数2。那么图1.11所示的走势基本可以说是f(n)=n3的象限图，增加的系数形成的象限图只不过是f(n)=n3的渐近线（如图1.11所示的红色线），对应的函数就是渐近函数，将一系列表示时间复杂度的渐近函数用T(n)来表示，就变成了如下形式（k表示系数）：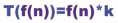

前面提过，系数k并不影响函数走势，所以这里可以忽略k的值，最终T(n)可以写成如下形式：

这种形式就是大O表示法，f(n)是T(n)的大O表示法。其中的O(f(n))就是这段代码的渐近函数的时间复杂度，简称时间复杂度，也就是T(n)。通过上面对算法时间复杂度的分析，总结出这样一条结论，在计算任何算法的时间复杂度时，可以忽略所有低次幂和最高次幂的系数，这样可以简化算法分析，并使注意力集中在增长率上。（2）第二段代码的时间复杂度：第二段代码有2层for循环，忽略系数，它的时间复杂度就是T(n)=n2，最终的时间复杂度f(n)=O(n2)，这段代码的复杂度的走势如图12所示。

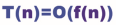
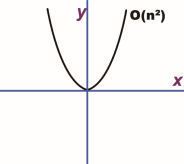
图12 平方象限图

例如：这样一段代码：

求这段代码的时间复杂度T(n)，分析如下：（1）蓝色的时间复杂度是T1(n)=3（3条语句）（2）红色的时间复杂度是T2(n)=n*n*3=n2*3（2层for嵌套循环乘以3条语句）（3）橙色的时间复杂度是T3(n)=n*2（1层for循环乘以2条语句）（4）绿色的时间复杂度是T4(n)=1（1条语句）（5）这段程序的时间复杂度是T(n)= T1(n)+ T2(n)+ T3(n)+ T4(n)=3+n2*3+n*2+1= n2*3+n*2+4 根据大O表示法推导形式（忽略所有低次幂和最高次幂的系数，包括常数），最终的大O表示法是T(n)=O(n2)。象限图和图1.12所示的一样。 2 常见的几个大O表示法第1小节介绍了常见大O表示法的两种示例，即如图11所示的T(n)=O(n3)和如图12所示的T(n)=O(n2)，在算法中，常见的大O表示法如表1所示。

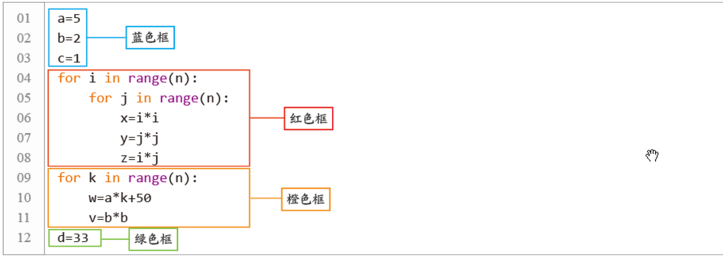
表1 常见的大O表示法

大 O 表示法	名称	对应算法例子
O(1)	常数时间	单个语句，例如赋值语句、输出语句等
O(log n)	对数时间	包含二分算法
O(n)	线性时间	包含检查查找，例如一层for循环等
O(n*log n)	对数线性时间	包含快速排序，一种速度较快的排序
O(n2)	平方时间	包含选择排序，一种速度比较慢的排序
O(n3)	立方时间	包含3层的for循环
O(n!)	阶乘时间	一种速度非常慢的排序
O(2n)	指数时间	适用于列出所有的排列或者组合

说明：表格的最后一列中提到的排序会在后续章节介绍。