我是如何用「最大公约数」秒杀算法题的

关于最大公约数有专门的研究。而在 LeetCode 中虽然没有直接让你求解最大公约数的题目。但是却有一些间接需要你求解最大公约数的题目。

比如：

• 914. 卡牌分组^[1]
• 365. 水壶问题^[2]
• 1071. 字符串的最大公因子^[3]

因此如何求解最大公约数就显得重要了。

如何求最大公约数？

定义法

def GCD(a: int, b: int) -> int:
    smaller = min(a, b)
    while smaller:
        if a % smaller == 0 and b % smaller == 0:
            return smaller
        smaller -= 1

「复杂度分析」

• 时间复杂度：最好的情况是执行一次循环体，最坏的情况是循环到 smaller 为 1，因此总的时间复杂度为 ，其中 N 为 a 和 b 中较小的数。
• 空间复杂度：。

辗转相除法

如果我们需要计算 a 和 b 的最大公约数，运用辗转相除法的话。首先，我们先计算出 a 除以 b 的余数 c，把问题转化成求出 b 和 c 的最大公约数；然后计算出 b 除以 c 的余数 d，把问题转化成求出 c 和 d 的最大公约数；再然后计算出 c 除以 d 的余数 e，把问题转化成求出 d 和 e 的最大公约数。..... 以此类推，逐渐把两个较大整数之间的运算转化为两个较小整数之间的运算，直到两个数可以整除为止。

def GCD(a: int, b: int) -> int:
    return a if b == 0 else GCD(b, a % b)

「复杂度分析」

• 时间复杂度：
• 空间复杂度：空间复杂度取决于递归的深度，因此空间复杂度为

更相减损术

辗转相除法如果 a 和 b 都很大的时候，a % b 性能会较低。在中国，《九章算术》中提到了一种类似辗转相减法的 更相减损术^[4]。它的原理是：两个正整数 a 和 b（a>b），它们的最大公约数等于 a-b 的差值 c 和较小数 b 的最大公约数。。

def GCD(a: int, b: int) -> int:
    if a == b:
        return a
    if a < b:
        return GCD(b - a, a)
    return GCD(a - b, b)

上面的代码会报栈溢出。原因在于如果 a 和 b 相差比较大的话，递归次数会明显增加，要比辗转相除法递归深度增加很多，最坏时间复杂度为 O(max(a, b)))。这个时候我们可以将辗转相除法和更相减损术做一个结合，从而在各种情况都可以获得较好的性能。

形象化解释

下面我们对上面的过程进行一个表形象地讲解，实际上这也是教材里面的讲解方式，我只是照搬过来，增加一下自己的理解罢了。我们来通过一个例子来讲解：

假如我们有一块 1680 米 * 640 米 的土地，我们希望讲起分成若干正方形的土地，且我们想让正方形土地的边长尽可能大，我们应该如何设计算法呢？

实际上这正是一个最大公约数的应用场景，我们的目标就是求解 1680 和 640 的最大公约数。

将 1680 米 * 640 米 的土地分割，相当于对将 400 米 * 640 米 的土地进行分割。为什么呢？假如 400 米 * 640 米分割的正方形边长为 x，那么有 640 % x == 0，那么肯定也满足剩下的两块 640 米 * 640 米的。

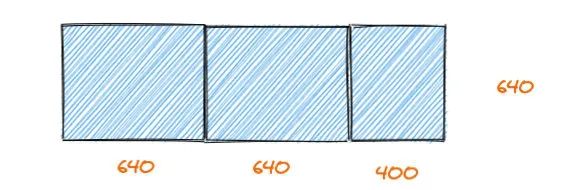
我们不断进行上面的分割：

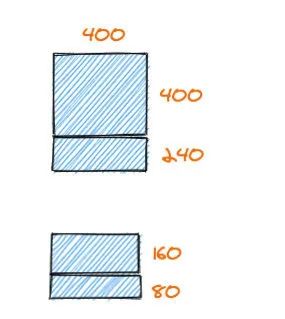
直到边长为 80，没有必要进行下去了。

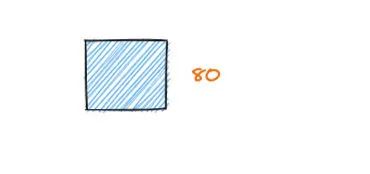
实例解析

题目描述

给你三个数字 a，b，c，你需要找到第 n 个（n 从 0 开始）有序序列的值，这个有序序列是由 a，b，c 的整数倍构成的。

比如：
n = 8
a = 2
b = 5
c = 7

由于 2，5，7 构成的整数倍构成的有序序列为 [1, 2, 4, 5, 6, 7, 8, 10, 12, ...]，因此我们需要返回 12。

注意：我们约定，有序序列的第一个永远是 1。

思路

大家可以通过 这个网站^[5] 在线验证。

一个简单的思路是使用堆来做，唯一需要注意的是去重，我们可以使用一个哈希表来记录出现过的数字，以达到去重的目的。

代码：

ss Solution:
    def solve(self, n, a, b, c):
        seen = set()
        h = [(a, a, 1), (b, b, 1), (c, c, 1)]
        heapq.heapify(h)

        while True:
            cur, base, times = heapq.heappop(h)
            if cur not in seen:
                n -= 1
                seen.add(cur)
            if n == 0:
                return cur
            heapq.heappush(h, (base * (times + 1), base, times + 1))

对于此解法不理解的可先看下我之前写的 几乎刷完了力扣所有的堆题，我发现了这些东西。。。（第二弹） ^[6]

然而这种做法时间复杂度太高，有没有更好的做法呢？

实际上，我们可对搜索空间进行二分。首先思考一个问题，如果给定一个数字 x，那么有序序列中小于等于 x 的值有几个。

答案是 x // a + x // b + x // c 吗？

❝

// 是地板除

❞

可惜不是的。比如 a = 2, b = 4, n = 4，答案显然不是 4 // 2 + 4 // 4 = 3，而是 2。这里出错的原因在于 4 被计算了两次，一次是 ，另一次是 。

为了解决这个问题，我们可以通过集合论的知识。

一点点集合知识：

• 如果把有序序列中小于等于 x 的可以被 x 整除，且是 a 的倍数的值构成的集合为 SA，集合大小为 A
• 如果把有序序列中小于等于 x 的可以被 x 整除，且是 b 的倍数的值构成的集合为 SB，集合大小为 B
• 如果把有序序列中小于等于 x 的可以被 x 整除，且是 c 的倍数的值构成的集合为 SC，集合大小为 C

那么最终的答案就是 SA ，SB，SC 构成的大的集合（需要去重）的中的数字的个数，也就是：

问题转化为 A 和 B 集合交集的个数如何求？

❝

A 和 B，B 和 C， A 和 C ，甚至是 A，B，C 的交集求法都是一样的。

❞

实际上， SA 和 SB 的交集个数就是 x // lcm(A, B)，其中 lcm 为 A 和 B 的最小公倍数。而最小公倍数则可以通过最大公约数计算出来：

def lcm(x, y):
    return x * y // gcd(x, y)

接下来就是二分套路了，二分部分看不懂的建议看下我的二分专题^[7]。

代码（Python3）

class Solution:
    def solve(self, n, a, b, c):
        def gcd(x, y):
            if y == 0:
                return x
            return gcd(y, x % y)

        def lcm(x, y):
            return x * y // gcd(x, y)

        def possible(mid):
            return (mid // a + mid // b + mid // c - mid // lcm(a, b) - mid // lcm(b, c) - mid // lcm(a, c) + mid // lcm(a, lcm(b, c))) >= n

        l, r = 1, n * max(a, b, c)
        while l <= r:
            mid = (l + r) // 2
            if possible(mid):
                r = mid - 1
            else:
                l = mid + 1
        return l

「复杂度分析」

• 时间复杂度：。
• 空间复杂度：gcd 和 lcm 的递归树深度，基本可忽略不计。

总结

通过这篇文章，我们不仅明白了最大公约数的「概念以及求法」。也形象化地感知到了最大公约数计算的「原理」。最大公约数和最小公倍数是两个相似的概念， 关于最大公约数和最小公倍数的题目在力扣中不算少，大家可以通过「数学标签」找到这些题。更多关于算法中的数学知识，可以参考这篇文章刷算法题必备的数学考点汇总 ^[8]

❝

这篇文章的第二篇也马上要发布了。

❞

Reference