适合对神经网络了解不多的同学,深入浅出的讲解了神经网络的核心思想,是一篇入门深度学习的好文。本文节选自“神经网络浅讲”。两层神经网络是本文的重点,因为正是在这时候,神经网络开始了大范围的推广与使用。Minsky说过单层神经网络无法解决异或问题。但是当增加一个计算层以后,两层神经网络不仅可以解决异或问题,而且具有非常好的非线性分类效果。不过两层神经网络的计算是一个问题,没有一个较好的解法。1986年,Rumelhar和Hinton等人提出了反向传播(Backpropagation,BP)算法,解决了两层神经网络所需要的复杂计算量问题,从而带动了业界使用两层神经网络研究的热潮。目前,大量的教授神经网络的教材,都是重点介绍两层(带一个隐藏层)神经网络的内容。 这时候的Hinton还很年轻,30年以后,正是他重新定义了神经网络,带来了神经网络复苏的又一春。图19 David Rumelhart(左)以及 Geoffery Hinton(右)
两层神经网络除了包含一个输入层,一个输出层以外,还增加了一个中间层。此时,中间层和输出层都是计算层。我们扩展上节的单层神经网络,在右边新加一个层次(只含有一个节点)。
现在,我们的权值矩阵增加到了两个,我们用上标来区分不同层次之间的变量。例如ax(y)代表第y层的第x个节点。z1,z2变成了a1(2),a2(2)。下图给出了a1(2),a2(2)的计算公式。
图20 两层神经网络(中间层计算)
计算最终输出z的方式是利用了中间层的a1(2),a2(2)和第二个权值矩阵计算得到的,如下图。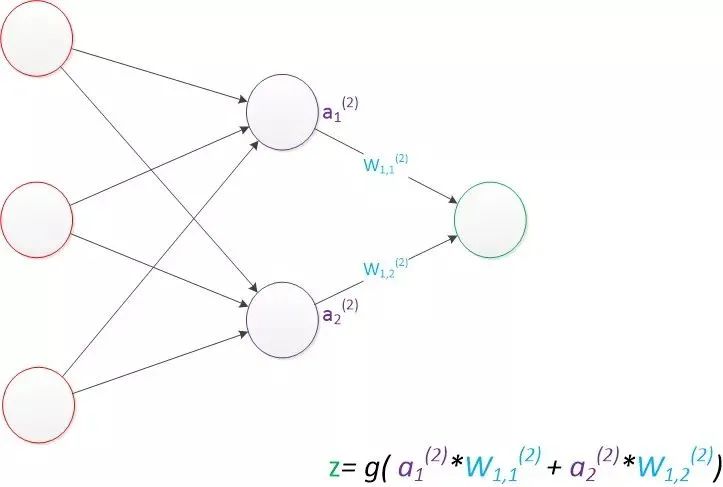
图21 两层神经网络(输出层计算)
假设我们的预测目标是一个向量,那么与前面类似,只需要在“输出层”再增加节点即可。
我们使用向量和矩阵来表示层次中的变量。a(1),a(2),z是网络中传输的向量数据。W(1)和W(2)是网络的矩阵参数。如下图。
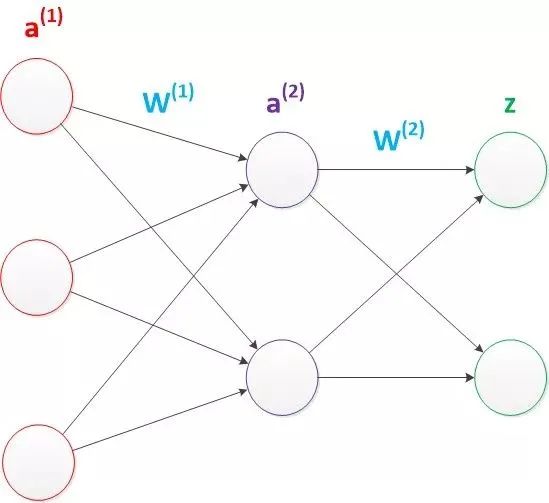
图22 两层神经网络(向量形式)
g(W(1) * a(1)) = a(2);
g(W(2) * a(2)) = z;
由此可见,使用矩阵运算来表达是很简洁的,而且也不会受到节点数增多的影响(无论有多少节点参与运算,乘法两端都只有一个变量)。因此神经网络的教程中大量使用矩阵运算来描述。需要说明的是,至今为止,我们对神经网络的结构图的讨论中都没有提到偏置节点(bias unit)。事实上,这些节点是默认存在的。它本质上是一个只含有存储功能,且存储值永远为1的单元。在神经网络的每个层次中,除了输出层以外,都会含有这样一个偏置单元。正如线性回归模型与逻辑回归模型中的一样。偏置单元与后一层的所有节点都有连接,我们设这些参数值为向量b,称之为偏置。如下图。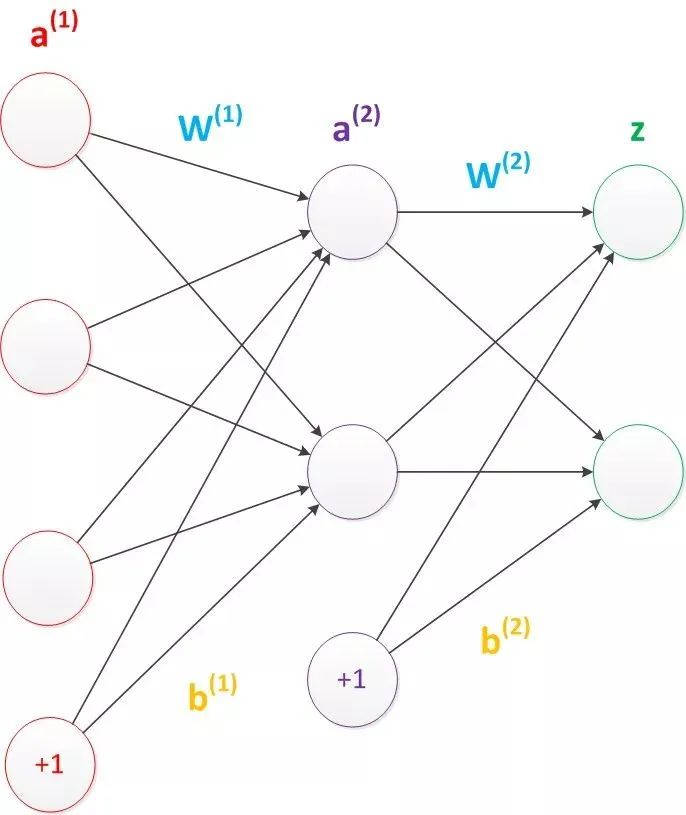
可以看出,偏置节点很好认,因为其没有输入(前一层中没有箭头指向它)。有些神经网络的结构图中会把偏置节点明显画出来,有些不会。一般情况下,我们都不会明确画出偏置节点。 g(W(1) * a(1) + b(1)) = a(2);
g(W(2) * a(2) + b(2)) = z;
需要说明的是,在两层神经网络中,我们不再使用sgn函数作为函数g,而是使用平滑函数sigmoid作为函数g。我们把函数g也称作激活函数(active function)。事实上,神经网络的本质就是通过参数与激活函数来拟合特征与目标之间的真实函数关系。初学者可能认为画神经网络的结构图是为了在程序中实现这些圆圈与线,但在一个神经网络的程序中,既没有“线”这个对象,也没有“单元”这个对象。实现一个神经网络最需要的是线性代数库。与单层神经网络不同。理论证明,两层神经网络可以无限逼近任意连续函数。这是什么意思呢?也就是说,面对复杂的非线性分类任务,两层(带一个隐藏层)神经网络可以分类的很好。下面就是一个例子(此两图来自colah的博客),红色的线与蓝色的线代表数据。而红色区域和蓝色区域代表由神经网络划开的区域,两者的分界线就是决策分界。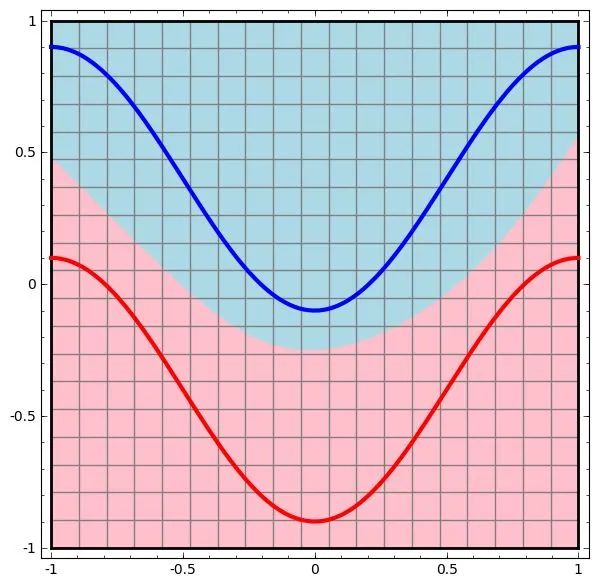
可以看到,这个两层神经网络的决策分界是非常平滑的曲线,而且分类的很好。有趣的是,前面已经学到过,单层网络只能做线性分类任务。而两层神经网络中的后一层也是线性分类层,应该只能做线性分类任务。为什么两个线性分类任务结合就可以做非线性分类任务?我们可以把输出层的决策分界单独拿出来看一下。就是下图。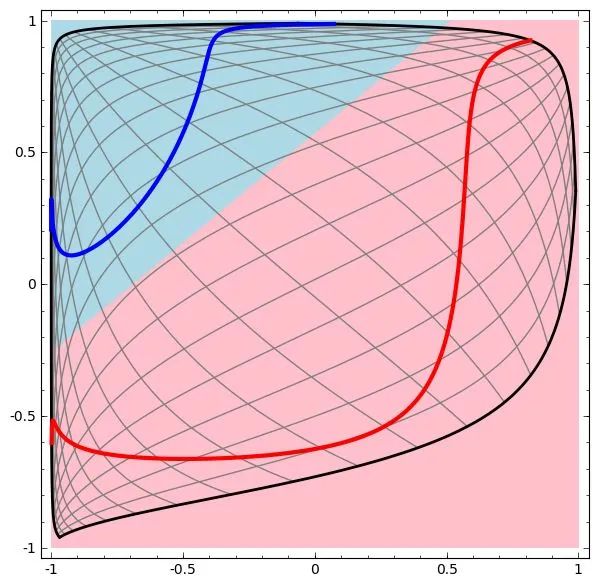
可以看到,输出层的决策分界仍然是直线。关键就是,从输入层到隐藏层时,数据发生了空间变换。也就是说,两层神经网络中,隐藏层对原始的数据进行了一个空间变换,使其可以被线性分类,然后输出层的决策分界划出了一个线性分类分界线,对其进行分类。这样就导出了两层神经网络可以做非线性分类的关键--隐藏层。联想到我们一开始推导出的矩阵公式,我们知道,矩阵和向量相乘,本质上就是对向量的坐标空间进行一个变换。因此,隐藏层的参数矩阵的作用就是使得数据的原始坐标空间从线性不可分,转换成了线性可分。两层神经网络通过两层的线性模型模拟了数据内真实的非线性函数。因此,多层的神经网络的本质就是复杂函数拟合。下面来讨论一下隐藏层的节点数设计。在设计一个神经网络时,输入层的节点数需要与特征的维度匹配,输出层的节点数要与目标的维度匹配。而中间层的节点数,却是由设计者指定的。因此,“自由”把握在设计者的手中。但是,节点数设置的多少,却会影响到整个模型的效果。如何决定这个自由层的节点数呢?目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值,通过切换这几个值来看整个模型的预测效果,选择效果最好的值作为最终选择。这种方法又叫做Grid Search(网格搜索)。了解了两层神经网络的结构以后,我们就可以看懂其它类似的结构图。例如EasyPR字符识别网络架构(下图)。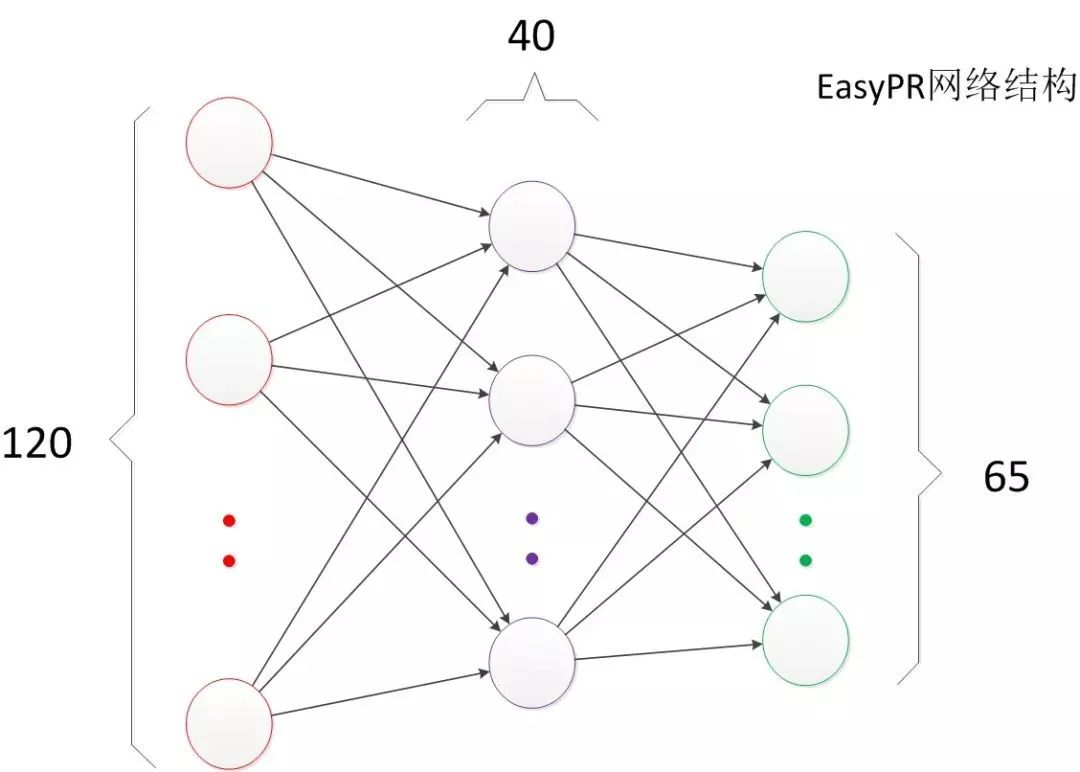
EasyPR使用了字符的图像去进行字符文字的识别。输入是120维的向量。输出是要预测的文字类别,共有65类。根据实验,我们测试了一些隐藏层数目,发现当值为40时,整个网络在测试集上的效果较好,因此选择网络的最终结构就是120,40,65。在Rosenblat提出的感知器模型中,模型中的参数可以被训练,但是使用的方法较为简单,并没有使用目前机器学习中通用的方法,这导致其扩展性与适用性非常有限。从两层神经网络开始,神经网络的研究人员开始使用机器学习相关的技术进行神经网络的训练。例如用大量的数据(1000-10000左右),使用算法进行优化等等,从而使得模型训练可以获得性能与数据利用上的双重优势。机器学习模型训练的目的,就是使得参数尽可能的与真实的模型逼近。具体做法是这样的。首先给所有参数赋上随机值。我们使用这些随机生成的参数值,来预测训练数据中的样本。样本的预测目标为yp,真实目标为y。那么,定义一个值loss,计算公式如下。loss = (yp - y)2
这个值称之为损失(loss),我们的目标就是使对所有训练数据的损失和尽可能的小。如果将先前的神经网络预测的矩阵公式带入到yp中(因为有z=yp),那么我们可以把损失写为关于参数(parameter)的函数,这个函数称之为损失函数(loss function)。下面的问题就是求:如何优化参数,能够让损失函数的值最小。此时这个问题就被转化为一个优化问题。一个常用方法就是高等数学中的求导,但是这里的问题由于参数不止一个,求导后计算导数等于0的运算量很大,所以一般来说解决这个优化问题使用的是梯度下降算法。梯度下降算法每次计算参数在当前的梯度,然后让参数向着梯度的反方向前进一段距离,不断重复,直到梯度接近零时截止。一般这个时候,所有的参数恰好达到使损失函数达到一个最低值的状态。在神经网络模型中,由于结构复杂,每次计算梯度的代价很大。因此还需要使用反向传播算法。反向传播算法是利用了神经网络的结构进行的计算。不一次计算所有参数的梯度,而是从后往前。首先计算输出层的梯度,然后是第二个参数矩阵的梯度,接着是中间层的梯度,再然后是第一个参数矩阵的梯度,最后是输入层的梯度。计算结束以后,所要的两个参数矩阵的梯度就都有了。反向传播算法可以直观的理解为下图。梯度的计算从后往前,一层层反向传播。前缀E代表着相对导数的意思。
反向传播算法的启示是数学中的链式法则。在此需要说明的是,尽管早期神经网络的研究人员努力从生物学中得到启发,但从BP算法开始,研究者们更多地从数学上寻求问题的最优解。不再盲目模拟人脑网络是神经网络研究走向成熟的标志。正如科学家们可以从鸟类的飞行中得到启发,但没有必要一定要完全模拟鸟类的飞行方式,也能制造可以飞天的飞机。优化问题只是训练中的一个部分。机器学习问题之所以称为学习问题,而不是优化问题,就是因为它不仅要求数据在训练集上求得一个较小的误差,在测试集上也要表现好。因为模型最终是要部署到没有见过训练数据的真实场景。提升模型在测试集上的预测效果的主题叫做泛化(generalization),相关方法被称作正则化(regularization)。神经网络中常用的泛化技术有权重衰减等。两层神经网络在多个地方的应用说明了其效用与价值。10年前困扰神经网络界的异或问题被轻松解决。神经网络在这个时候,已经可以发力于语音识别,图像识别,自动驾驶等多个领域。
历史总是惊人的相似,神经网络的学者们再次登上了《纽约时报》的专访。人们认为神经网络可以解决许多问题。就连娱乐界都开始受到了影响,当年的《终结者》电影中的阿诺都赶时髦地说一句:我的CPU是一个神经网络处理器,一个会学习的计算机。但是神经网络仍然存在若干的问题:尽管使用了BP算法,一次神经网络的训练仍然耗时太久,而且困扰训练优化的一个问题就是局部最优解问题,这使得神经网络的优化较为困难。同时,隐藏层的节点数需要调参,这使得使用不太方便,工程和研究人员对此多有抱怨。90年代中期,由Vapnik等人发明的SVM(Support Vector Machines,支持向量机)算法诞生,很快就在若干个方面体现出了对比神经网络的优势:无需调参;高效;全局最优解。基于以上种种理由,SVM迅速打败了神经网络算法成为主流。
神经网络的研究再次陷入了冰河期。当时,只要你的论文中包含神经网络相关的字眼,非常容易被会议和期刊拒收,研究界那时对神经网络的不待见可想而知。编辑:王菁
校对:汪雨晴











