统计学跟我们有关系吗?
作者 | 林骥
来源 | 公众号:林骥
《统计学关我什么事》,是一本关于「贝叶斯统计学」的超级入门书,作者小岛宽之,是日本的经济学博士,知名的数学随笔作家。作者运用简单的「面积图」和四则运算,就把复杂的统计学理论,讲得简单、生动、有趣,十分值得学习。

01
一个例子
书中举了一个很有趣的例子,假如有位女同事给你送了一盒巧克力,你推测她把你当成「真命天子」的概率有多大?
根据贝叶斯推理的方法,只需要简单的 3 步,就能算出这个概率。
第一步
先假设女同事把你当成「真命天子」的概率为10%,这个概率可以根据自己的主观感受进行修改;
第二步
通过调查统计知道,职场女性对「真命天子」送出巧克力的平均概率为42.5%,对「无关路人」送出巧克力的平均概率为22%;
第三步
根据女同事送巧克力的行为,计算她把你当成「真命天子」的概率 = 10%*42.5% / (10%*42.5% + 90%*22%) = 17.67%。
也就是说,当你认为女同事对你有意思的可能性比较低时,即使她送了巧克力给你,也只是增加了她对你有意思的概率,但并不能因此说明她对你真的有意思。
02
矩阵树图
为了直观地展现上述推理过程的概率分布情况,作者林骥用 pyecharts 制作了一张矩阵树图:
# 导入库from pyecharts import options asoptsfrom pyecharts.charts importTreeMapfrom pyecharts.globals importThemeType# 真命天子的概率a = 0.1# 无关路人的概率b = 1 - a# 送给真命天子的概率c = 0.425# 不送真命天子的概率d = 1 - c# 送给无关路人的概率e = 0.22# 不送无关路人的概率f = 1 - e# 定义数据data = [{"value": 100,"name": "后验概率","children": [{"value": 100,"name": "送巧克力","children": [{"value": round(a*c/(a*c+b*e)*100,2), "name": "送给真命天子"},{"value": round(b*e/(a*c+b*e)*100,2), "name": "送给无关路人"},],}],},{"value": 100,"name": "先验概率","children": [{"value": 100,"name": "条件概率","children": [{"value": round(a*c*100,2), "name": "送给真命天子"},{"value": round(a*d*100,2), "name": "不送真命天子"},{"value": round(b*e*100,2), "name": "送给无关路人"},{"value": round(b*f*100,2), "name": "不送无关路人"},],}],},]# 绘制矩形树图c = (TreeMap(init_opts=opts.InitOpts(width='800px', height='800px', theme=ThemeType.LIGHT)).add("推测送巧克力的女同事的心意",data,levels=[opts.TreeMapLevelsOpts(treemap_itemstyle_opts=opts.TreeMapItemStyleOpts(border_color="#00589F", border_width=4, gap_width=4)),opts.TreeMapLevelsOpts(color_saturation=[0.3, 0.5],treemap_itemstyle_opts=opts.TreeMapItemStyleOpts(border_color_saturation=0.7, gap_width=2, border_width=2),),opts.TreeMapLevelsOpts(color_saturation=[0.3, 0.5],treemap_itemstyle_opts=opts.TreeMapItemStyleOpts(border_color_saturation=0.6, gap_width=1),),opts.TreeMapLevelsOpts(color_saturation=[0.3, 0.5]),],).set_global_opts(title_opts=opts.TitleOpts(title="推测送巧克力的女同事的心意,她把你当成真命天子的概率是"+'%.2f%%' % (a*c/(a*c+b*e)*100),pos_left="center", pos_top="30",)).render("推测送巧克力的女同事的心意.html"))
运行结束之后,用浏览器打开新生成的 HTML 文件,就能看到一个矩阵树图。
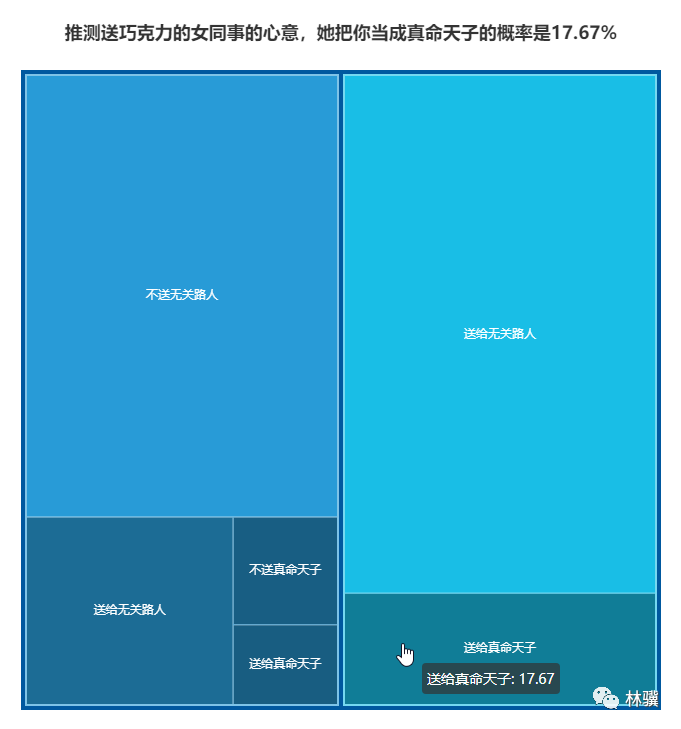
你可以自己修改代码中的概率数据,运行得到不同的计算结果,甚至可以做成动态变化的图,动态展现概率的变动。
你也可以把上面制作矩阵树图的方法,应用到其他的工作场景,比如:替换掉那些分类比较多的饼图。
03
小结
贝叶斯推理的魅力和优势在于,即使没有事前的客观数据,也能根据主观判断进行推算。
而且在数据比较少的情况下,也可以应用贝叶斯推理,当数据越多,推测的结果就越准确。
把有用的知识,与有趣的场景相结合,这是一种非常好的学习方法。
知识的分享,最好能既有用又有趣,这样效果更好,而且让人更容易坚持下去。
随着因特网技术的的发展,贝叶斯统计在商业领域得到了成功的应用。
比尔·盖茨曾经说过:
微软之所以在激烈的市场竞争中胜出,正是由于采用了贝叶斯统计。
世界上有很多著名的投资人,包括巴菲特在内,都在运用「贝叶斯统计」的方法。
而运用贝叶斯统计的核心理念,就是持续去做大概率正确的事情,日积月累,成功的概率就会越来越大。
作者:林骥
来源:公众号林骥
原文链接:
https://mp.weixin.qq.com/s/08U0madY2INhrKnW27Jvfw
封面图来源于unsplash
推荐阅读:

统计无用论?来看看统计学在大数据中的价值(上)

数据越多越好,到底是不是悖论?(下)

数据驱动背后的“陷阱”

TalkingData——用数据说话
每天一篇好文章,欢迎分享关注