前言

相信各位前端小伙伴在日常工作中不免会涉及到使用 JavaScript 处理数值相关的操作，例如数值计算、保留指定小数位、接口返回数值过大等等，这些操作都有可能导致原本正常的数值在 JavaScript 中确表现得异常（即精度丢失），这也是被很多开发者诟病的一点（你该不会还没踩过坑吧！），当然包括很多后端开发者（不止一次的被问到这个问题）。

本文主要包含精度丢失场景、精度丢失原因、解决方案等方面的内容，文中若有不正确的地方欢迎在评论区分享你的见解。

精度丢失场景

浮点数的计算

数值计算在前端的应用还不算少，但涉及浮点数参与计算时可能会出现精度丢失，如下：

加（ + ）

正常计算：0.1 + 0.2 = 0.3
JavaScript 计算：0.1 + 0.2 = 0.30000000000000004

减（ - ）

正常计算：1 - 0.9 = 0.1
JavaScript 计算：1 - 0.9 = 0.09999999999999998

**乘（ * ）**

正常计算：0.0532 * 100 = 5.32
JavaScript 计算：0.0532 * 100 = 5.319999999999999

除（ / ）

正常计算：0.3 / 6 = 0.05
JavaScript 计算：0.3 / 6 = 0.049999999999999996

超过最值

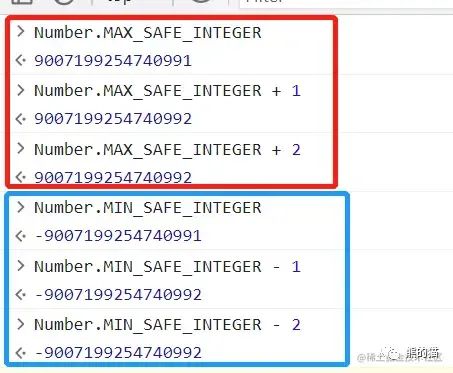
所谓超过最值（最大、最小值）指的是超过了 Number.MIN_SAFE_INTEGER（- 9007199254740991），即

+（2^53 – 1）或 Number.MAX_SAFE_INTEGER（+ 9007199254740991），即 -（2^53 – 1）范围的值，项目中最常见的就是如下几种情况：

后端返回的数值超过最值

例一，后端返回的列表数据，通常都会有相应的 ID 来标识唯一性，但后端字啊生成这个 ID 时是 Long 类型，那么该值很可能就会超过 JavaScript 中能表示的最大正整数，此时就导致精度丢失，即前端实际获取到的 ID 值和后端返回的将不一致
例二，后端可能需要将一些值通过计算之后，把对应的结果值返回给前端，此时若该值超过了最值，那么也会产生精度丢失

前端进行数值计算时，计算结果超过最值

保留指定小数位

除了上述对涉及浮点数计算、超过最值的场景之外，我们通常还会对数值进行保留指定小数位的处理，而部分开发者可能会直接使用 Number.prototype.toFixed 来实现，但这个方法却并不能保证我们期望的效果，例如保留小数位时需要进行四舍五入时就会有问题，如下：

console.log(1.595.toFixed(2)) // 1.59 ——> 期望为：1.60console.log(1.585.toFixed(2)) // 1.58 ——> 期望为：1.59console.log(1.575.toFixed(2)) // 1.57 ——> 期望为：1.58console.log(1.565.toFixed(2)) // 1.56 ——> 期望为：1.57console.log(1.555.toFixed(2)) // 1.55 ——> 期望为：1.56console.log(1.545.toFixed(2)) // 1.54 ——> 期望为：1.55console.log(1.535.toFixed(2)) // 1.53 ——> 期望为：1.54console.log(1.525.toFixed(2)) // 1.52 ——> 期望为：1.53console.log(1.515.toFixed(2)) // 1.51 ——> 期望为：1.52console.log(1.505.toFixed(2)) // 1.50 ——> 期望为：1.51

精度丢失的原因

计算机内部实际上只能存储/识别 二进制，因此文档、图片、数字等都会被转换为二进制，而对于数字而言，虽然我们看到的是十进制的表示结果，但实际上会底层会进行十进制和二进制的相互转换，而这个转换过程就有可能会出现精度丢失，因为十进制转二进制后可能产生无限循环部分，而实际存储空间是有限的。

IEEE 754 标准

Javascript 中的数字存储使用了 IEEE 754 中规定的双精度浮点数数据类型，双精度浮点数使用 64 位（8 字节） 来存储一个浮点数，可以表示二进位制的 53 位 有效数字，即 (0-52 位为 1) 111...111 = (53 位为 1，0-52 位为 0) 1000...000 - 1，也就是 2^53 - 1，而这也就是 JavaScript 中 Number.MAX_SAFE_INTEGER（+ 9007199254740991） 对应的值。

双精度浮点数的组成

双精度浮点数（double） 由如下几部分组成：

sign 符号位，0 为正，1 为负

占 1bit，在 63 位

exponent 指数部分，表示 2 的几次方

占 11bit，在 52-62 位
指数采用偏移码表示法，即将指数的真实值 e 加上一个偏移量，然后得到阶码（即计算结果）并将其表示为二进制数
其中偏移量 = (2^n-1) - 1，n 是指数的位数（即 n = 11），因此偏移量为 Math.pow(2, 11-1) - 1 = 1023
阶码 E = 指数真值 e + 偏移码 (2^n-1) - 1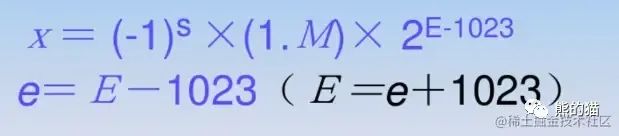

mantissa 尾数部分，表示浮点数的精度

占 52bit，在 0-51 位
尾数采用隐式的方式表示，即在尾数的最高位上总是隐含着一个 1，并且隐藏在小数点的左边 (即 1 < 尾数 < 2)，因此尾数的有效位数为 53 位，而不是 52 位

十进制浮点数的存储过程

有了上面的公式，接下来我们来演示一下一个十进制浮点数是如何以双精度浮点数的形式被存储到计算机中的，其大致分为如下两步：

十进制转二进制

分别对整数部分和小数部分的十进制转化为二进制

求出 sign、exponent、mantissa 的值

下面我们通过 263.3 这个数值来演示。

十进制转二进制

分别将 263.3 的整数部分 263 和小数部分 0.3 转为对应的二进制数，这里你可以使用便捷的 在线转换工具，也可选择手动计算：

整数部分转二进制

一直除以 2 直到余数为 0 或出现循环，然后从下往上将每次的余数进行组合即可

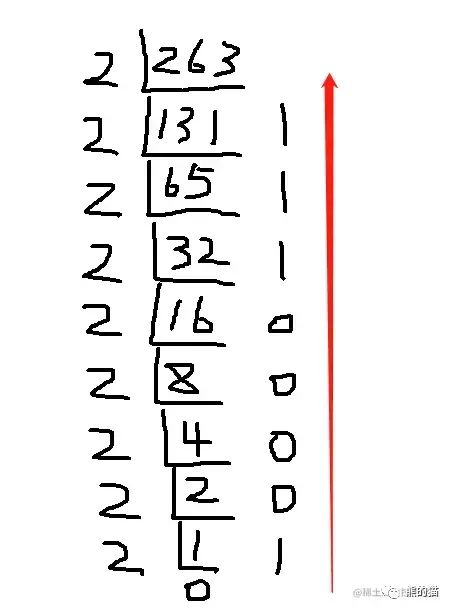
小数部分转二进制

一直乘以 2 直到乘积为 1 或出现循环，然后从上往下将每次的乘积的整数位进行组合即可

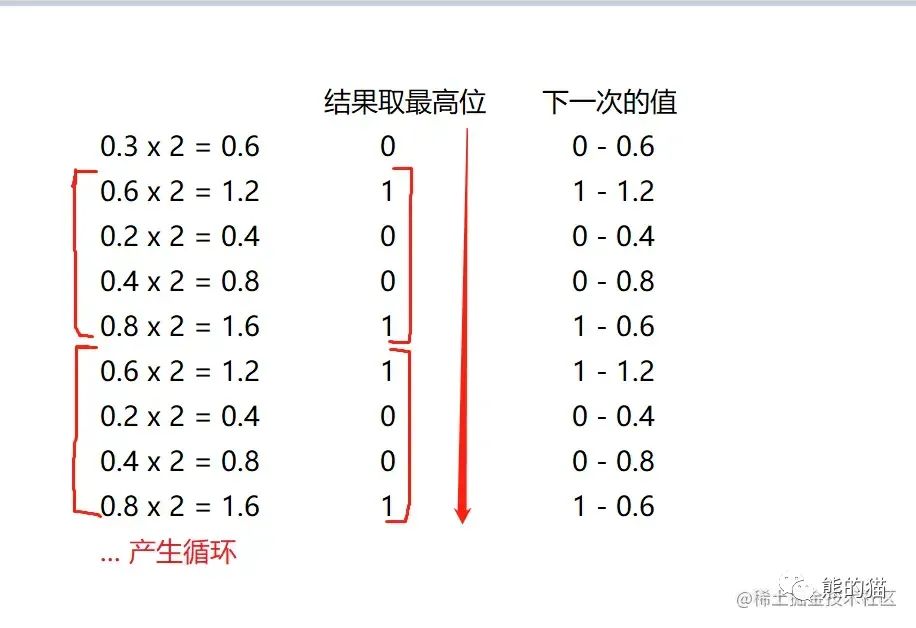
最终得到的结果就是 263.3(10) 对应的二进制为 100000111.010011001...

求出 sign、exponent、mantissa 的值

求 sign

其中 sign 为符号位，且 263.3(10) 为正数，因此 sign = 0

求 exponent

根据公式 (-1)^S x (1. M) x 2^(E-1023) 可知，其中的尾数要符合 1. M 的形式，因此 100000111.010011001... 中小数点需要往左移动 8位变成 1.00000111 010011001 ...
其中的 8 就是指数真值，但在实际存储时是存阶码的二进制，根据公式阶码 = 指数真值(8) + 偏移量(1023)，即阶码 = 1031，所以 exponent 值就为 1031 的二进制：10000000111

求 mantissa

根据上一步的 1.00000111 010011001 ... 很容易知道尾数 mantissa = 00000111 010011001 ...

最终存储形式

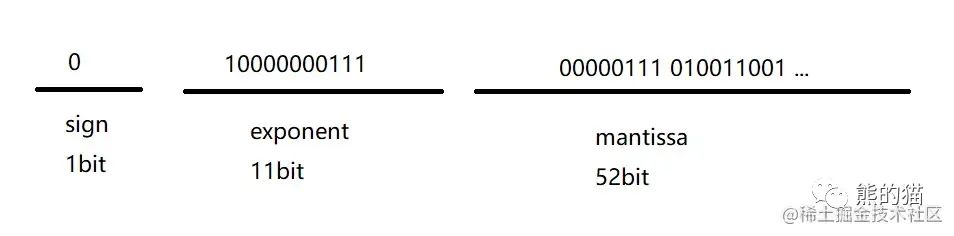
Number.prototype.toFixed 的舍入

关于这个方法的舍入方式，目前最多的说法就是银行家算法，的确在大多情况下确实能够符合银行家算法的规则，但是部分情况就并不符合其规则，因此严格意义上来讲 Number.prototype.toFixed 并不算是使用了 银行家算法，如果你要问为什么，请看 ECMAScript® 2024 Language Specification (tc39.es)，在下文都会提及。

银行家算法

所谓银行家算法用一句话概括为：

四舍六入五考虑，五后 有数 就进一，五后 无数看 奇偶，五前 为偶当 舍去，五后 为奇要 进一

四舍指保留位后的数值 < 5 应 舍去，4 只是个代表值
六入指保留位后的数值 > 5 应 进一，6 只是个代表值
若保留位后的数值 = 5，看 5 后是否有数

若 5 后无数，则看 5 前的数值的奇偶来判断

若 5 前的数值为偶数，则舍去
若 5 前的数值为奇数，则进一

若 5 后有数，则进一

用例子来验证一下：

// 四舍(1.1341).toFixed(2) = '1.13'
// 六入(1.1361).toFixed(2) = '1.14'
// 五后 有数 ，进一(1.1351).toFixed(2) = '1.14'
// 五后 无数，看奇偶，五前为 3 奇数，进一 (1.1350).toFixed(2) = '1.14'
// 五后 无数，看奇偶，五前为 0 偶数，舍去(1.1050).toFixed(2) = '1.10'

看起来没有问题是吧！

// 五后 有数，应进一(1.1051).toFixed(2) = 1.11 （正确 √）(1.105).toPrecision(17) = '1.1050000000000000' // 精度
// 五后 无数，看奇偶，五前为 0 偶数，应舍去(1.105).toFixed(2) = 1.10 （正确 √）
// 五后 无数，看奇偶，五前为 2 偶数，应舍去(1.125).toFixed(2) = 1.13 （不正确 ×）1.125.toPrecision(17) = '1.1250000000000000' // 精度
// 五后 无数，看奇偶，五前为 4 偶数，应舍去(1.145).toFixed(2) = 1.15 （不正确 ×）1.145.toPrecision(17) = '1.1450000000000000' // 精度
// 五后 无数，看奇偶，五前为 6 偶数，应舍去(1.165).toFixed(2) = 1.17 （不正确 ×）1.165.toPrecision(17) = '1.1650000000000000' // 精度
// 五后 无数，看奇偶，五前为 8 偶数，应舍去(1.185).toFixed(2) = 1.19 （不正确 ×）1.185.toPrecision(17) = '1.1850000000000001' // 精度

ECMAScript 定义的 toFixed 标准

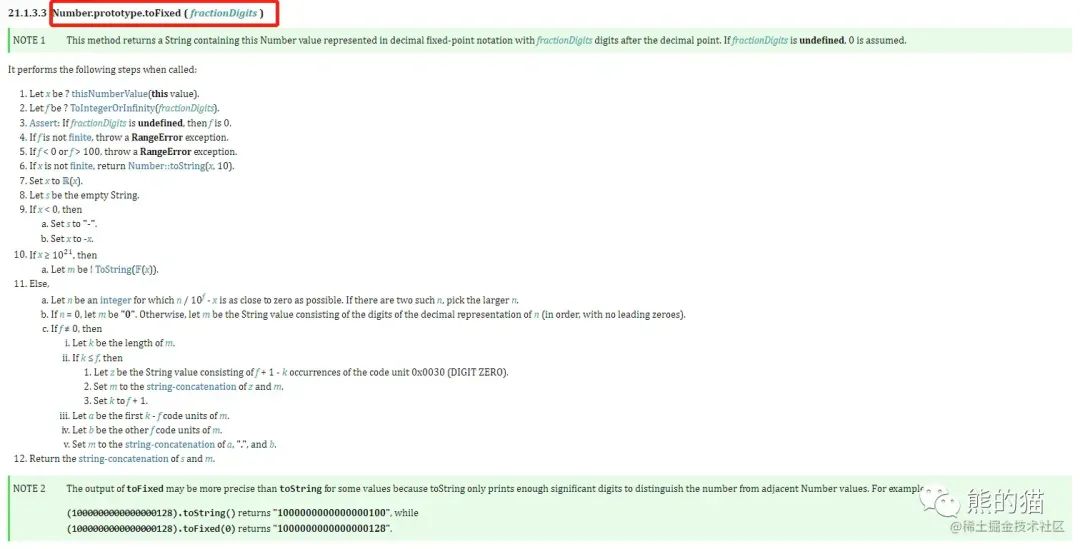
一眼望上去是不是觉得看不懂，那么这里就来尝试解释一下这个标准的内容吧（掺杂个人理解）！

让 x = 目标数字，如：(1.145).toFixed(2) 中 x = 1.1245
让 f = 参数，如：(1.145).toFixed(2) 中 f = 2
若 f = undefined，即未传参，则将 f = 0
若 f = Infinite，即传入了无穷值，则抛出 RangeError 异常
若 f < 0 或 f > 100，即传入了不在 0 - 100 之间的值，则抛出 RangeError 异常
若 x = Infinite，即想要对非准确值保留位操作，则返回其字符串形式

例如，Infinity.toFixed(2) = 'Infinity'、NaN.toFixed(2) = 'NaN'

让 x = 计算机所能表示的数学值 ℝ(x)

从数字或 BigInt x 到数学值的转换表示为 x 的数学值，或 ℝ（x）

让返回值符号 s = ''，即为符号定义初始值
若 x < 0，则将 s = '-'，并将 x = -x
若 x ≥ 10^21，则返回值 m = x 对应的科学计数法表示的字符串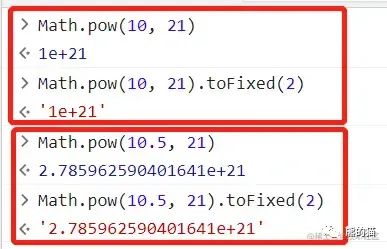
若 x < 10^21，则
a. 让 n = 一个整数，其中 n / 10^f - x 尽可能接近于 0，如果有两个这样的 n，选择较大的 n
b. 若 n = 整数 0，则 m = "0"，否则，m = 由 n 的 十进制 表示形式的数字组成的 字符串值（按顺序，不带前导零）
c. 若指数 f ≠ 0，则 k = m.length
- 若 k ≤ f，则
- z = 由代码单元 0x0030（DIGIT ZERO） 的 f+1-k 次出现组成的 字符串

- m = z + m

- k = f + 1

- 让 a = m 的第一个 k-f 码单元

- 让 b = m 的其它 f 个编码单元

- 将 m = a + "." + b

12. 返回 s + m 组成的字符串

看不懂？那就挑懂的地方看

不多说了，还是用 (1.125).toFixed(2) = 1.13 举个栗子吧！

根据上述规范初始 x = 1.125，f = 2，s = ''
根据规范 7 可知 x = 1.125.toPrecision(53) = 1.125
根据规范 11.a 提供的公式：n / 10^f - x ≈ 0 代入计算：n ≈ 112.5：

此时最接近 n 的整数有两个值为 110 和 112，按标准取最大的 113
在按 11.c 的规范得到 m = 1.13

最终返回 s + m= 1.13

还不会，再来个 (-1.105).toFixed(2) = -1.10 的栗子吧！

根据上述规范初始 x = 1.105，f = 2，s = '-'
根据规范 7 可知 x = (-1.105).toPrecision(53) = 1.10499...
根据规范 11.a 提供的公式：n / 10^f - x ≈ 0 代入计算：n ≈ 110.4...：

此时最接近 n 的整数只有一个值为 110（因为只有小数点后为 5 时，向上 / 向下取整才会有两种情况）
在按 11.c 的规范得到 m = 1.10

最终返回 s + m= -1.13

如何解决前端数值的精度问题？

虽然知道了精度丢失的原因，也知道了 toFixed 舍入的逻辑，但是实际上在进行计算时，我们还是希望按照实际看到的数值来进行计算或舍入，而不是底层转换过的值。

使用第三方库

需要的自行查阅：

math.js
big.js
bignumber.js
decimal.js

思路扩展

浮点数计算

浮点数在 JavaScript 中经底层转换后可能会有精度丢失，但是安全范围内的整数却不会丢失，那么我们就可以先将浮点数转成整数进行计算后，再将计算结果成为浮点数。

以 0.1 + 0.2 = 0.30000000000000004 举个例子，如下：

原式：0.1 + 0.2 = x
扩大 10 倍：0.1 * 10 + 0.2 * 10 = 10 * x
变式：10 * x = 3
结果：x = 0.3

超过最值

前面提到的后端返回或前端计算产生的超过安全范围的值，我们可以使用 BigInt 来处理，这是新增的原始值类型，它提供了一种方法来表示大于 2^53 - 1 的整数。

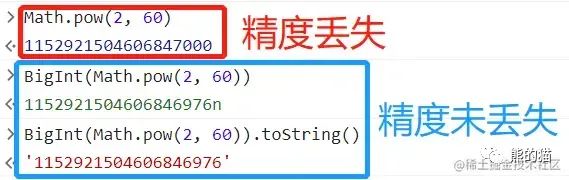
保留指定小数位

既然 Number.prototype.toFixed() 的舍入方法并不是我们需要的，那么我们可以直接将其重写成符合的即可，例如：

Number.prototype.toFixed=function (d) {     var s=this+"";     if(!d)d=0;     if(s.indexOf(".")==-1)s+=".";     s+=new Array(d+1).join("0");     if(new RegExp("^(-|\\+)?(\\d+(\\.\\d{0,"+(d+1)+"})?)\\d*$").test(s)){        var s="0"+RegExp.$2,pm=RegExp.$1,a=RegExp.$3.length,b=true;        if(a==d+2){            a=s.match(/\d/g);             if(parseInt(a[a.length-1])>4){                for(var i=a.length-2;i>=0;i--){                    a[i]=parseInt(a[i])+1;                    if(a[i]==10){                        a[i]=0;                        b=i!=1;                    }else break;                }            }            s=a.join("").replace(new RegExp("(\\d+)(\\d{"+d+"})\\d$"),"$1.$2");         }if(b)s=s.substr(1);         return (pm+s).replace(/\.$/,"");    }return this+""; }

最后

以上就是本文的全部内容了，由于涉及到部分内容计网相关内容，所以可能理解起来会比较吃力，但是跨过这道坎也就没那么难理解了。

希望本文对你有所帮助！！！

前端社群

下方加 Nealyang 好友回复「加群」即可。

如果你觉得这篇内容对你有帮助，我想请你帮我2个小忙：

1. 点个「在看」，让更多人也能看到这篇文章

后端问为什么前端数值精度会丢失？

前言

精度丢失场景

浮点数的计算

加（ + ）

减（ - ）

乘（ * ）

除（ / ）

超过最值

保留指定小数位

精度丢失的原因

IEEE 754 标准

双精度浮点数的组成

十进制浮点数的存储过程

十进制转二进制

求出 sign、exponent、mantissa 的值

最终存储形式

Number.prototype.toFixed 的舍入

银行家算法

ECMAScript 定义的 toFixed 标准

看不懂？那就挑懂的地方看

如何解决前端数值的精度问题？

使用第三方库

思路扩展

浮点数计算

超过最值

保留指定小数位

最后

**乘（ * ）**